Спектральная плотность составного импульсного сигнала

Сигнал на рис. 7.19 можно рассматривать как сумму f₁ (t) + f₂ (t)

Спектр прямоугольного импульса, симметрично расположенного относительно 0 = t , уже найден ранее. В этом примере можно воспользоваться линейностью преобразования Фурье и его свойствами, определяющими влияние смещения сигнала. S₁ (t) смещен относительно изображения на t₁ = - t / 2.

.

Свойство: (при смещении сигнала f(t) на t₀)

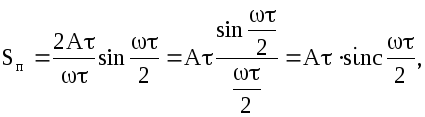
Отрицательный импульс S₂ (t) получается из импульса, изображенного на рис. 7.19 путем смещения в сторону запаздывания на t₂ = t / 2 и умножения на (-1).

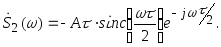
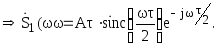
Используя линейность преобразования Фурье: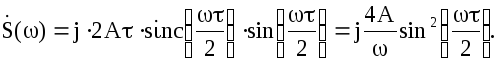

Дальнейшее упрощение связано с преобразованием по формуле Эйлера.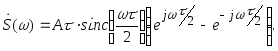

График изображен на рис. 7.20.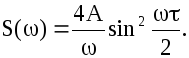

Сопоставим прямое преобразование Фурье с формулой преобразования по Лапласу:

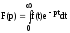
при условии, что f(t) = 0 при t<0.

Формулы для спектра функции S (jw) могут быть получены из соответствующих формул изображений по Лапласу, если в последних р заменить на jw .

Пример. Найти спектр функции

полагая, что f(t) = 0 при t<0 и построим S(w).

Решение:

Найдем изображение по Лапласу

Заменим р на jw и получим спектр

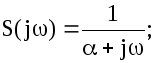
S(jw) – комплексная величина, равная S (w) e^jjs . Модуль ее равен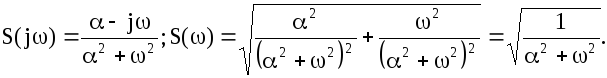

Аргумент j_s = arctg (- w / k ) .

Графики представлены на рисунке 7.21.

Рис. 7.21

Применение спектрального метода

Спектральный (частотный) метод исследования процессов в электрических цепях особенно широко применяется при рассмотрении вопросов прохождения модулированных колебаний через усилители, фильтры и др. Устройства, в импульсной технике при рассмотрении вопросов прохождении через 4-х полюсники коротких импульсов длительностью порядка нескольких микросекунд.

Пусть на вход 4-х полюсника с передаточной функцией k(jw)=k(w) e^jj(w) при нулевых начальных условиях воздействует сигнал f₁ (t) имеющий спектр S_вх (jw) . На выходе 4-х полюсника появится сигнал f₂ (t) , спектр которого

Где

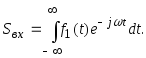
Предполагается, что сигнал можно изменить по амплитуде, запаздывающей по t, однако форма сигнала (в котором заключена информация) сохраняется.

f₂ (t) можно представить f₂ (t) = a f₁ (t-t₀). Если к f₂ (t) применить преобразование Фурье, то окажется, что спектр f₂ (t):

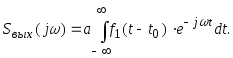
Действительно:

Введем t₁ = t – t₀ , тогда

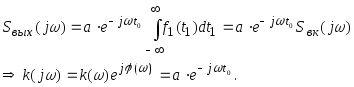
т.е. для прохождения импульса или модулированного колебания через 4-х полюсник без искажения формы необходимо, чтобы модуль передаточной функции не зависел от функции частоты, а аргумент j(w) = - w (t₀) линейно изменялся в функции частоты. В реальных 4-х полюсниках эти условия могут быть выполнены лишь приближенно в некоторой полосе частот, которую называют полосой пропускания. Для того, чтобы при прохождении через 4-х полюсник не изменил своей формы, необходимо, чтобы важнейшие гармонические составляющие частного спектра сигнала находились внутри полосы пропускания 4-х полюсника.

T.к. в полосе пропускания идеальные условия для прохождения импульса все же не выполняются, то, проходя через четырех полюсник, импульс в какой то степени искажается.

Определить стпепнь искажения можно на основании прямого и обратного преобразования Фурье.

Основные этапы способа таковы:

1. Нахождение спектра U₁ (jw) входного сигнала u₁ (t);

2. Определение передаточной функции 4-хполюсника K(jw);

3. Получение спектра выходного сигнала u₂ (jw) = k (jw)u(jw);

4. Определение u₂ (t) по u₂ (jw).

Пример

На вход RC цепи рис. 7.22 (а) подается импульс u(t) в виде равнобедренного треугольника, продолжительностью t_и , имеющий амплитуду u.

Найти спектральную плотность выходного U₂ (jw) на емкости. Построить АЧХ U₂ (jw) если U = 20 В, r =100 Дж; С = 1 мкФ. T_и= 1мс

Решение:

U(t)

U

t_и/2 t_и t

(б)

R

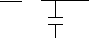
C

(а)

Рис. 7.22

.

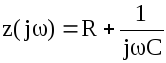
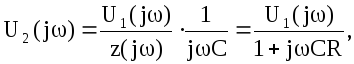
Найдем U₁ (t) двумя способами.

1 способ.

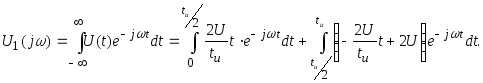
После интегрирования: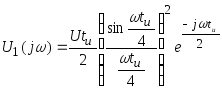

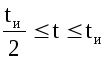
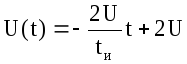
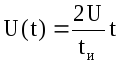
Находим U₂ (jw):

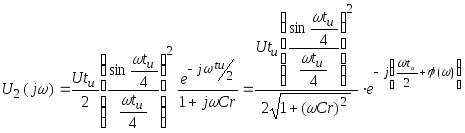
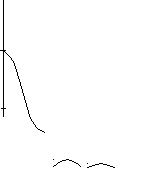
2 способ:

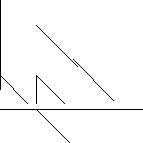
Рис. 7.24

Заданное U может быть представлено в виде наложения 3-х прямых: первая начинается в точке t = 0 и действует неограниченно долго, вторая имеет отрицательный наклон, крутизну в 2 раза больше чем крутизна первой прямой и начинается в точке t_n /2 , третья имеет такой же наклон, как и прямая 1, но начинается в точке t_n .

Уравнение напряжения прямой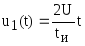

Изображение по Лапласу

С учетом теорем операционного исчисления изображения прямых 2 и 3: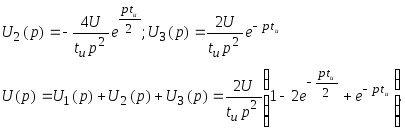

Заменим р на jw , получим спектральную плотность суммарного импульса входного напряжения.

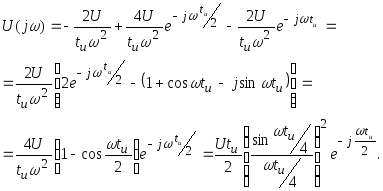
См. 1 способ – тот же результат.