Общая схема применения метода комплексных амплитуд.

Анализ цепей методом комплексных амплитуд содержит следующие этапы:

1. Замена гармонических токов и напряжений всех ветвей их комплексными изображениями, а эквивалентной схемы цепи для мгновенных значений – комплексной схемой замещения;

2. Составление уравнений электрического равновесия цепи для комплексных изображений токов и напряжений на основе законов Ома и Кирхгофа в комплексной форме;

3. Решение системы уравнений электрического равновесия относительно комплексных изображений интересующих токов и напряжений;

4. Переход от комплексных изображений искомых токов и напряжений к их оригиналам.

Пример 1: рассмотрим токи и напряжения в схеме.

i R

.

E L

C

Рис.2.8.

Решение:

Для схемы уравнения для мгновенных значений можно записать так u_R+u_L+u_C=E или

Если записать в комплексной форме:

Следовательно,

Комплексная схема замещения представлена на рис.2.9.

.

E

.

E

Рис.2.9.

Комплексное сопротивление можно представить не в алгебраической форме, а в показательной:

Уравнение представляет собой закон Ома в

комплексной форме.

Зная ток, не составляет труда нахождение напряжения на элементах цепи:

Если предположить, что х_L>х_C, то векторная диаграмма примет следующий вид (см. рис.2.10). Цепь имеет резистивно-индуктивный характер.

Im

>0

Re

Im

Re

Рис.2.10.

Пример 2: Определить комплексное входное сопротивление и комплексный ток в последовательной RLC-цепи с параметрами:

L=80 мкГн, C=500 пФ, R=100 Ом; к зажимам которой приложено напряжение U=2_*10_*cos(wt) для частот w₁=2,5*10⁶, w₂=8*10⁶, w3=5*10⁶ рад/с.

Решение:

Комплексное входное сопротивление цепи

(1)

равно сумме комплексных сопротивлений входящих в нее элементов. Подставляя в (1) параметры элементов цепи, находим комплексное сопротивление цепи при интересующих значениях частоты внешнего воздействия:

Таким образом, при w=w₁ входное сопротивление цепи имеет резистивно-емкостной характер, при w=w₂ – резистивно-индуктивный, при w=w₃ – чисто резистивный.

Используя закон Ома в комплексной форме, находим комплексный ток в цепи:

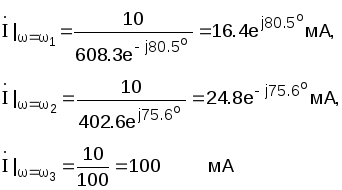
(опережает по фазе)

(отстает)

(совпадает по фазе с ) .

Комплексные частотные характеристики.

Комплексной частотной характеристикой (КЧХ) цепи называется отношение комплексных изображений отклика и воздействия.

Модуль КЧХ равен отношению амплитуд или действующих значений отклика цепи и внешнего воздействия, а ее аргумент представляет собой разность начальных фаз отклика и внешнего воздействия.

Зависимость модуля H_k(w) и аргумента _k(w) называется амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристиками цепи.

При графическом представлении КЧХ обычно строят отдельно АЧХ и ФЧХ.

КЧХ делят на входные и передаточные. Когда отклик и внешнее воздействие рассматриваются на одних и тех же зажимах цепи, КЧХ называют входной, если на разных – передаточной.

К передаточным характеристикам цепи относят:

• комплексный коэффициент передачи по напряжению

• комплексный коэффициент передачи по току

• комплексное передаточное сопротивление

• комплексная передаточная проводимость

КЧХ линейных цепей не зависят от амплитуды и начальной фазы внешнего воздействия, а определяются структурой цепи и параметрами входящих в нее элементов.

Пример: Определим АЧХ и ФЧХ передаточной функции по напряжению простейшего RC-фильтра в режиме холостого хода.