Лекции по ТОЭ10 / PART3-2

10

Классификация фильтров.

Классификация по пропускаемым частотам.

Рассмотрим схему простейшей RC цепи (см. рис 3.20).

Рис.3.20 RC фильтр

Определим для данной схемы частотный коэффициент передачи по напряжению , по отношению к выходным зажимам данная RC цепь является простым делителем напряжения. Поэтому:

,

где - постоянная времени цепи.

Амплитудно-частотная характеристика (АЧХ): и фазо-частотная характеристика (ФЧХ): _{(см.рис.3.21).Цепи с подобными АЧХ мало ослабляют НЧ колебания и сильно подавляют колебания с ВЧ. Такие цепи являются фильтрами низких частот (ФНЧ).}

_{Если выходным сигналом служит напряжение на резисторе: ; ; ; (см. рис. 3.22).}

Такие цепи являются фильтрами верхних частот (ФВЧ). Они обладают свойствами противоположными свойствам ФНЧ. То есть пропускаются ВЧ колебания и подавляются НЧ колебания.

|k(w)|

|k(w)|

w

w

Рис.3.21 АЧХ RC цепи при съёме выходного напряжения с конденсатора

Рис.3.22 АЧХ RC цепи при съёме выходного напряжения с резистор

а

Рассмотрим частотный коэффициент передачи по напряжению фильтра Вина (см. рис. 3.23).

Рис.3.23 Фильтр Вина

Импеданс последовательной цепи: _.

Импеданс параллельного соединения R и С: , где w=RC.

, _.

_{(см. рис. 3.24).}

Рис.3.24 АЧХ фильтра Вина

На низких и высоких частотах фильтр Вина имеет малые значения модуля коэффициента передачи напряжения. Максимум, равный 0.33 достигается при w=1. Такая цепь, пропускающая в нагрузку лишь узкую полосу частот, называется полосовым фильтром.

Следующая цепь представляет собой режекторный или заграждающий фильтр, реализованный в виде “перекрёстного” фильтра (см. рис. 3.25).

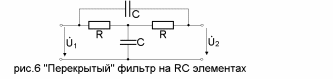
Рис.3.25 “Перекрытый” фильтр на RC элементах

Найдём частотный коэффициент передачи напряжения , считая, что порт 2 находится в режиме холостого хода, а к порту 1 подключён источник ЭДС . Воспользовавшись известными методами определим для данного четырёхполюсника

, где w= RC.

АЧХ данной цепи:

(см. рис. 3.26).

Подобные фильтры, уменьшающие амплитуду колебаний в пределах некоторого конечного интервала, часто называют режекторными фильтрами. Таким образом по пропускаемым частотам фильтры можно классифицировать на:

• ФВЧ;

• ФНЧ;

• полосовые;

• заграждающие.

Классификация по схемам звеньев

Фильтры могут состоять из Г, Т, П образных звеньев, мостовых и других. В зависимости от числа звеньев фильтр может быть однозвенным или многозвенным.

Рис.3.27. Четырехполюсники, представляющие собой Г-образные (а) Т-образные (б), П-образные (в) структуры.

Фильтры, в которых произведение произвольного продольного сопротивления на соответствующее поперечное, представляет собой некоторые постоянные для данного фильтра числа, не зависящие от частоты, принято называть «k»-фильтрами. z₁z₂=k², где k-вещественное число. Фильтры, в которых это произведение зависит от частоты называют «м»-фильтрами.

Разновидности ФНЧ прототипов.

На практике часто используются фильтры прототипы, каждый из которых обладает определенными преимуществами и недостатками с точки зрения частотно-избирательных свойств. В курсовой работе предлагается выбор из трех разновидностей: фильтр Баттерворта, фильтр Чебышева и эллиптический фильтр.

Чтобы приводимые в спектрах таблицы и графики имели большую общность, характеристики ФНЧ, ФВЧ, ПФ, РФ приводят к характеристикам эквивалентного ФНЧ прототипа.

Разновидности прототипов.

1 ) Фильтр Баттерворта.

АЧХ фильтра Баттерворта максимально плоская, без пульсаций. Аналитически задается выражением:

АЧХ, где - нормированная (относительная) частота, n - порядок фильтра (n примерно соответствует числу реактивных элементов). Увеличение порядка n приводит к улучшению характеристики, что видно из рисунка 3.28. Полином под знаком радикала (1+х²ⁿ) , где х = , называется полиномом Баттерворта.

Рис.3.28 АЧХ фильтра Баттерворта

2 )Фильтр Чебышева.

АЧХ фильтра Чебышева имеет колебания в полосе пропускания (это недостаток фильтра).Однако по сравнению с фильтром Баттерворта (того же порядка) АЧХ фильтра Чебышева

обладает большей крутизной переходного участка (прямоугольностью):

АЧХ , где

n - порядок фильтра,

-нормированная частота,

Т_n() - полином Чебышева,

- постоянное число.

Т_n имеет вид : Т_n (х) = cos( n arccos x). АЧХ достигает максимума в тех точках, где Т_n() =0. Размах пульсаций определяет параметр , а их число - степень n. Число пульсаций приблизительно равно n/2. обычно стремятся уменьшить. Размах АЧХ определяется выражением: .

АЧХ фильтра Чебышева представлена на рисунке 3.29.

Рис.3.29

_ГР

3) Фильтр Золотарёва (иногда называемый фильтром Кауэра или эллиптическим фильтром). АЧХ фильтр обладает по сравнению с предыдущими двумя фильтрами (для фильтров того же порядка) наилучшими частотно избирательными свойствами. Большей крутизной АЧХ на промежуточном участке между полосой пропускания и полосой задерживания. Вместе с тем существуют как в полосе пропускания, так и в полосе задерживания пульсации (см.рис.3.30).

Рис.3.30 АЧХ фильтра Кауэра

Для этих трёх фильтров-прототипов имеются справочники, где приводятся их схемы и параметры элементов. Каждый из указанных фильтров в определённом смысле оптимален. При этом заданную избирательность фильтр Чебышева обеспечивает при меньшем порядке чем фильтр Баттерворта, а эллиптический фильтр в этом смысле лучше фильтра Чебышева. В рамках курса «Электротехники» предлагается курсовая работа по проектированию аналоговых LC-фильтров. Методика расчёта и содержание отчёта изложены в [1;3;5].