4. Моделирование одномерных временных рядов

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Уровни временного ряда формируются из трендовой (Т), сезонной (S) и случайной (Е) компонент. Различают аддитивную и мультипликативную модель временного ряда. Построение модели сводится к нахождению компонент временного ряда для каждого уровня. Выбор одной из двух моделей проводится на основе анализа структуры сезонных колебаний. Если амплитуда колебаний уровней ряда примерно одинакова, то строят аддитивную модель, если же амплитуда колебаний увеличивается или затухает – мультипликативную. Наличие трендовой и сезонной составляющих возможно определить при помощи расчета коэффициентов автокорреляции уровней ряда.

Коэффициент автокорреляции первого порядка показывает тесноту линейной зависимости между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на один шаг во времени, и рассчитывается по формуле

, (4.1)

где , .

Коэффициент автокорреляции второго порядка характеризует силу линейной зависимости между уровнями ряда с шагом (лагом) в два временных промежутка и рассчитывается по формуле 4.2. Аналогично можно рассчитать коэффициент автокорреляции 3-го и более высоких порядков.

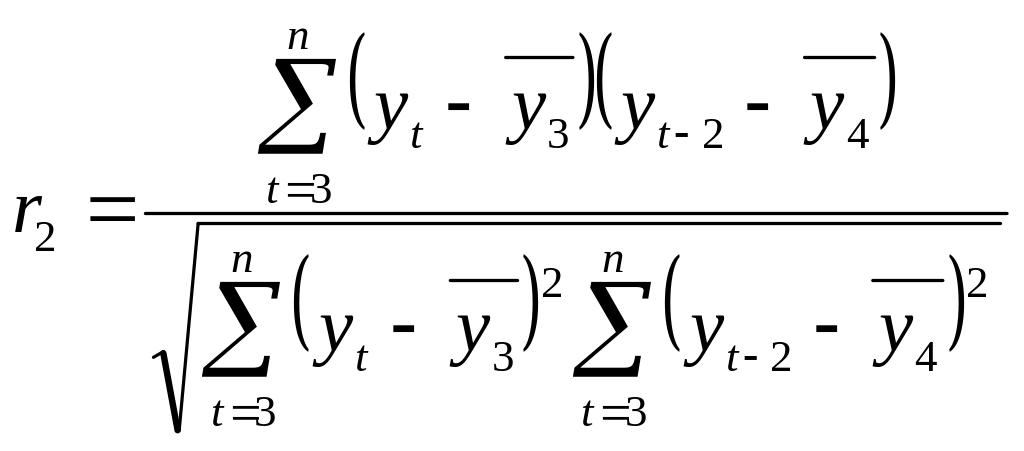, (4.2)

где , .

Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой. С помощью автокорреляционной функции можно выявить структуру ряда. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то временной ряд содержит линейную тенденцию. Если наиболее высоким оказался коэффициент порядка m, ряд содержит сезонные колебания с периодом m моментов времени. Если же ни один из коэффициентов не оказался значимым, то либо ряд содержит сильную нелинейную тенденцию, либо уровни ряда носят случайный характер. По коэффициентам автокорреляции уровней можно судить только о наличии линейной тенденции.

Построение аддитивной (мультипликативной) модели временного ряда начинают с поиска сезонных компонент. Если ряд содержит линейную тенденцию, сезонность можно выделить методом скользящей средней:

1. найти скользящие средние за каждые m периодов времени с шагом 1 период;

2. рассчитать центрированные скользящие средние как среднее значение между соседними скользящими средними;

3. найти оценки сезонных компонент как разность между исходными значениями ряда и центрированными скользящими средними (для аддитивной модели) или как частное (для мультипликативной модели);

4. привести оценки сезонных компонент в соответствие с номерами периодов времени в цикле. В результате каждому периоду будет соответствовать несколько значений оценок сезонных компонент;

5. для каждого периода времени рассчитать среднюю оценку сезонной компоненты ;

6. найти корректирующий коэффициент как среднее значение по средним оценкам сезонных компонент ;

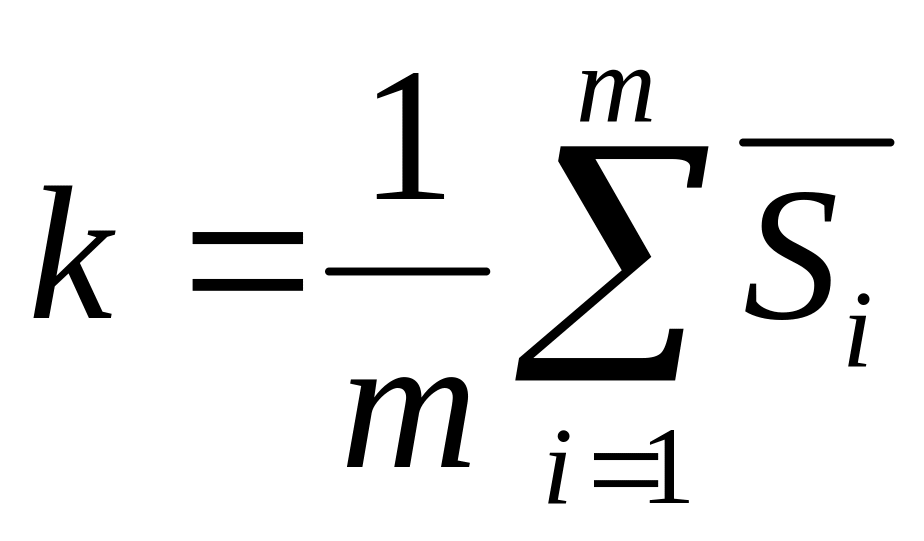7. рассчитать скорректированные значения сезонных компонент по формуле 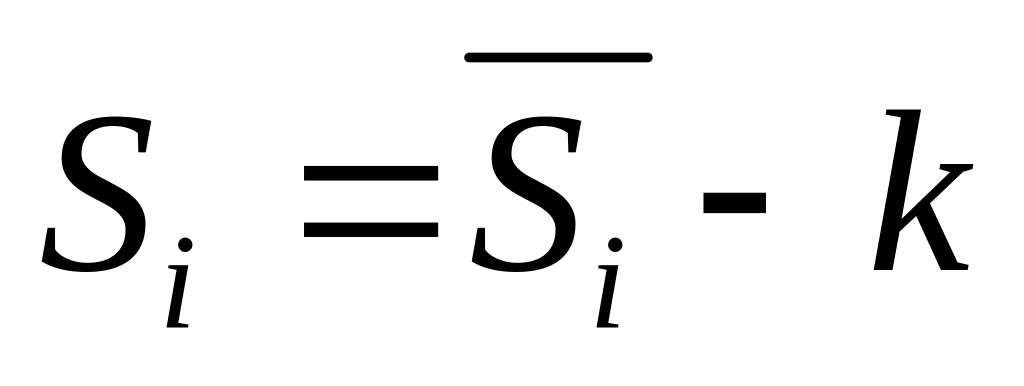(для аддитивной модели) и (для мультипликативной модели).

После расчета скорректированных значений сезонных компонент , их исключают из уровней ряда и проводят аналитическое выравнивание временного ряда, которое заключается в построении уравнения регрессии, характеризующего зависимость уровней ряда от фактора времени. Для построения уравнения тренда можно использовать различные виды функций: линейную , гиперболическую , экспоненциальную , степенную , параболу 2-го и более высоких порядков . Параметры перечисленных выше уравнений можно найти обычным методом наименьших квадратов, используя в качестве независимой переменной номер наблюдения t = 1, 2, …, n, а в качестве зависимой переменной – фактические уровни ряда y_t.

Одной из предпосылок Гаусса-Маркова для применения в расчетах метода наименьших квадратов является отсутствие автокорреляции остатков, т.е. значения остатков регрессии должны быть распределены независимо друг от друга. Наличие или отсутствие автокорреляции остатков целесообразно проверять при построении регрессии на временных рядах. Рассматривая последовательность остатков как временной ряд, можно построить график их зависимости от времени. Даже визуально при помощи графика нередко можно заметить наличие тенденции или циклических колебаний в остатках. Это свидетельствует о том, что каждое следующее значение остатков зависит от предшествующего. В этом случае говорят о наличии автокорреляции в остатках.

Для проверки остатков уравнения регрессии на автокорреляцию используют критерий Дарбина-Уотсона. Статистика Дарбина – Уотсона определяется по формуле (4.3).

(4.3)

Если автокорреляция отсутствует, то величина d должна быть близкой к двум в больших выборках. При наличии положительной автокорреляции d приближается к 0, отрицательной – к 4. Критическое значение d при любом данном уровне значимости зависит от числа объясняющих переменных в уравнении регрессии и от количества наблюдений в выборке. К сожалению, оно также зависит от конкретных значений, принимаемых объясняющими переменными. Поэтому невозможно составить таблицу с указанием точных критических значений для всех возможных выборок, как это можно сделать для t- и F-статистик; но можно вычислить верхнюю и нижнюю границы для критического значения d. Для положительного значения автокорреляции они обозначаются d_U и d_L.

Рис. 4.1. Значения статистики Дарбина-Уотсона

В зависимости от того, в каком из промежутков находится расчетное значение d, можно сделать определенный вывод (рис. 4.1). Значения статистик Дарбина-Уотсона d_U и d_L находят в таблицах по известному количеству наблюдений в выборке n и числу независимых факторов k. Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции в остатках.

Пример 4. Изучить структуру ряда, представленного в таблице 4.1. На его основе построить мультипликативную модель и рассчитать прогноз на 1 и 2 квартал следующего года.

Таблица 4.1

Временной промежуток	Номер квартала	Объем продаж, млн. руб.
	t	yt
1 квартал 1 года	1	170,1
2 квартал 1 года	2	67,4
3 квартал 1 года	3	76,8
4 квартал 1 года	4	126,1
1 квартал 2 года	5	157,7
2 квартал 2 года	6	60,9
3 квартал 2 года	7	70,7
4 квартал 2 года	8	119,6
1 квартал 3 года	9	143,3
2 квартал 3 года	10	57
3 квартал 3 года	11	65,9
4 квартал 3 года	12	109,1
1 квартал 4 года	13	130,4
2 квартал 4 года	14	52,1
3 квартал 4 года	15	58,1
4 квартал 4 года	16	101,7

Решение.

Для изучения структуры временного ряда объема продаж y_t построим график зависимости уровней ряда от фактора времени t (см. рис. 4.2). Визуальный анализ показывает наличие сезонных колебаний и убывающей линейной тенденции.

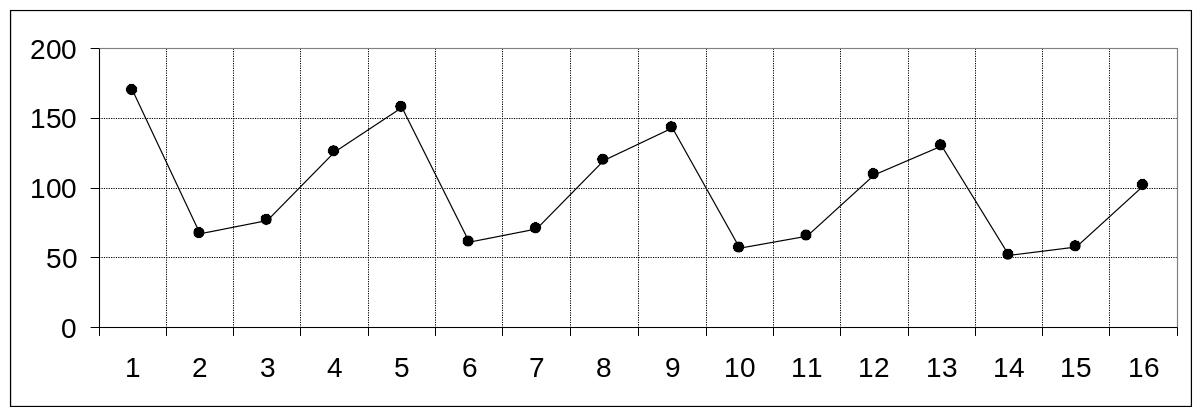
Рис. 4.2. График зависимости уровней ряда y_t от фактора t

Наличие сезонных колебаний подтверждает автокорреляционная функция и коррелограмма, изображенная на рис. 4.3.

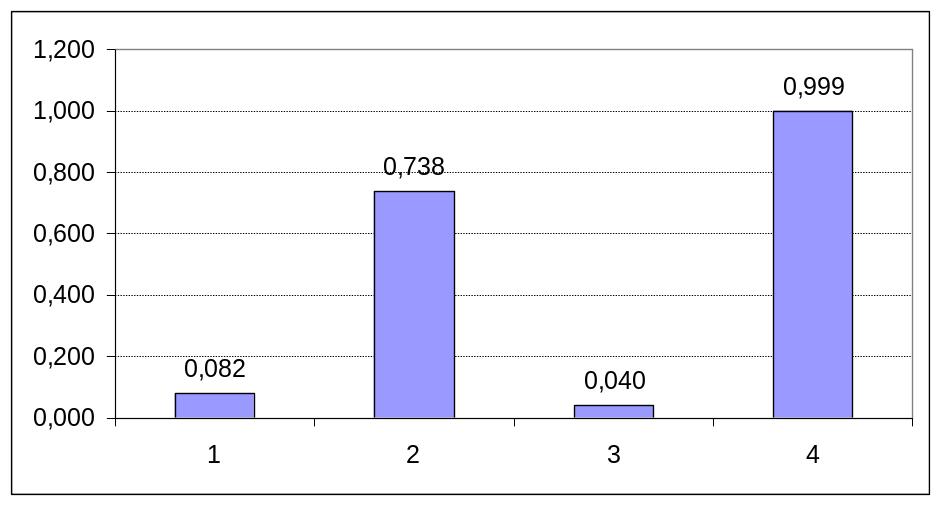
Рис. 4.3. Коррелограмма

Построим мультипликативную модель временного ряда объема продаж (см. табл. 4.2). Скользящие средние в графе 3 рассчитаны, как среднее арифметическое значений ряда за 1 – 4 квартал, 2 – 5 квартал, 3 – 6 квартал и т.д. Центрированные скользящие средние в графе 4 являются средними между парами соседних скользящих средних. Оценки сезонных компонент в графе 5 рассчитываем как частное от деления исходных значений ряда (графа 2) на центрированные скользящие средние (графа 4).

Таблица 4.2

№ квартала, t	Объем продаж, yt	Скользящая средняя за 4 квартала	Центрированные скользящие средние	Оценки сезонных компонент
1	2	3	4	5
1	170,1	–	–	–
2	67,4 76,8		–	–
		110,1 107
3	126,1 157,7		108,55 106,1875	0,708 1,188
		105,375 103,85
4	60,9 70,7		104,6125 103,0375	1,507 0,591
		102,225 98,625
5	119,6 143,3		100,425 98,1375	0,704 1,219
		97,65 96,45
6	57 65,9		97,05 95,1375	1,477 0,599
		93,825 90,6
7	109,1 130,4		92,2125 89,9875	0,715 1,212
		89,375 87,425
8	52,1 58,1		88,4	1,475
		85,575 110,1
9	101,7 170,1		108,55 106,1875	0,708 1,188
		107 105,375
10	67,4 76,8		104,6125 103,0375	1,507 0,591
		103,85 102,225
11	126,1 157,7		100,425 98,1375	0,704 1,219
		98,625 97,65
12	60,9 70,7		97,05 95,1375	1,477 0,599
		96,45 93,825
13	119,6 143,3		92,2125 89,9875	0,715 1,212
		90,6 89,375
14	57 65,9		88,4	1,475
		87,425
15	109,1 130,4		–	–
		–
16	52,1		–	–

На следующем этапе подготовим таблицу 4.3. Занесем в нее оценки сезонных компонент, распределив их по кварталам. Средние оценки сезонных компонент найдем как среднее арифметическое по каждой строке таблицы. Например, для 1-го квартала , для 2-го квартала и т.д. Корректирующий коэффициент рассчитан как среднее арифметическое средних оценок сезонных компонент , а скорректированные сезонные компоненты S_i получены путем деления значений на корректирующий коэффициент k.

Таблица 4.3

№ квартала	№ года				Средние оценки сезонных компонент,	Скорректированные сезонные компоненты, S i
	2001	2002	2003	2004
1 квартал		1,507	1,477	1,475	1,486	1,487
2 квартал		0,591	0,599	0,602	0,597	0,598
3 квартал	0,708	0,704	0,715		0,709	0,709
4 квартал	1,188	1,219	1,212		1,206	1,207
Корректирующий коэффициент					0,9997

Исключим сезонные компоненты из исходного ряда и получим выровненные значения объема продаж (табл. 4.4).

Таблица 4.4

t	y	S	y / S
1	170,1	1,487	114,4
2	67,4	0,598	112,8
3	76,8	0,709	108,3
4	126,1	1,207	104,5
5	157,7	1,487	106,1
6	60,9	0,598	101,9
7	70,7	0,709	99,7
8	119,6	1,207	99,1
9	143,3	1,487	96,4
10	57	0,598	95,4
11	65,9	0,709	93,0
12	109,1	1,207	90,4
13	130,4	1,487	87,7
14	52,1	0,598	87,2
15	58,1	0,709	82,0
16	101,7	1,207	84,3

В преобразованном ряду выделим линейный тренд методом наименьших квадратов. В качестве независимой переменной используем значения t, зависимой – y / S.

В результате получим модель линейного тренда ряда y_t:

Правильность расчетов предлагаем проверить самостоятельно при помощи известных формул вручную или с использованием компьютерных прикладных программ. Нами получена модель высокого качества, причем объем продаж ежеквартально снижается на 2 млн. 700 тыс. руб.

Проверим остатки модели на наличие автокорреляции при помощи критерия Дарбина-Уотсона. Для того, чтобы была возможность сравнить мультипликативную модель с другими моделями временного ряда, рассчитаем ошибки по формуле (табл. 4.5).

Таблица 4.5

t	yt	S	T
1	170,1	1,487	113,2	1,786	–	–	3,189
2	67,4	0,598	111,1	0,977	-0,809	0,654	0,954
3	76,8	0,709	109,1	-0,522	-1,499	2,246	0,272
4	126,1	1,207	107,0	-3,001	-2,480	6,149	9,008
5	157,7	1,487	104,9	1,686	4,688	21,973	2,843
6	60,9	0,598	102,9	-0,579	-2,265	5,129	0,335
7	70,7	0,709	100,8	-0,757	-0,178	0,032	0,573
8	119,6	1,207	98,7	0,480	1,237	1,531	0,231
9	143,3	1,487	96,7	-0,414	-0,894	0,799	0,171
10	57	0,598	94,6	0,466	0,879	0,773	0,217
11	65,9	0,709	92,5	0,308	-0,158	0,025	0,095
12	109,1	1,207	90,5	-0,038	-0,346	0,120	0,001
13	130,4	1,487	88,4	-1,013	-0,975	0,951	1,026
14	52,1	0,598	86,3	0,510	1,524	2,321	0,261
15	58,1	0,709	84,2	-1,627	-2,137	4,568	2,647
16	101,7	1,207	82,2	2,544	4,171	17,396	6,472
Сумма:						64,667	28,295

Коэффициент Дарбина-Уотсона равен: . Для 16 наблюдений и одной независимой переменной . Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину: . Поскольку 1,71 > 1,37, то можно утверждать, что в остатках регрессии автокорреляция отсутствует.

Рассчитаем прогноз объема продаж на 1 и 2 квартал 5-го года:

, ,

млн. руб., млн. руб.

Итак, в первом квартале следующего года следует ожидать объем продаж в размере 119 млн. 110 тыс. руб., а во втором квартале – 46 млн. 640 тыс. руб.