Вопрос 4 Параметры заторможенного потока

Параметры заторможенного потока – это параметры, которые получаются в потоке, если его полностью изоэнтропно затормозить.

Связь между статическими параметрами и параметрами заторможенного потока (их также называют полными параметрами) определяется уравнением изоэнтропного процесса

или ;

; .

Если применить уравнение сохранения энергии (уравнение движения, уравнение Бернулли) к сечению, в котором скорость потока уменьшается до нуля (т.е. поток полностью тормозится и энтальпия принимает максимальное значение), то можно записать

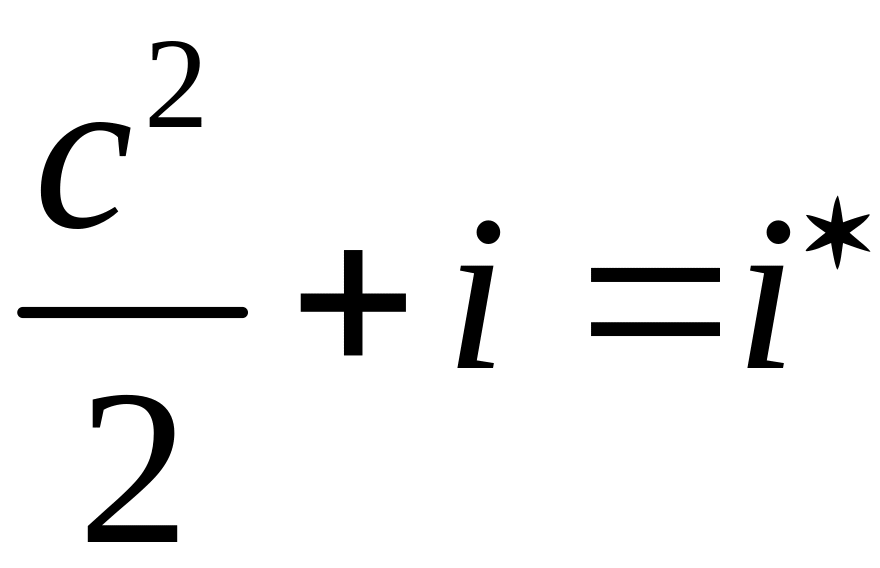=const (9)

или

=const или =const (10)

или

. (11)

В этих уравнениях

- удельная энтальпия заторможенного потока (полная удельная энергия потока), Дж/кг;

- термодинамические параметры заторможенного потока или параметры торможения, их называют также полная температура, полное давление и полная плотность.

Из формул видно, что для изоэнтропного потока параметры заторможенного потока остаются постоянными вдоль потока в то время как статические параметры изменяются. Например, температура заторможенного потока равна

=const,

т.е. повышение скорости в изоэнтропном потоке всегда сопровождается уменьшением статической температуры.

Для воздуха с_р≈1000 Дж/(кг∙К). Тогда

и .

с, м/с	100	350	1000
ΔТ, К(0С)	5	61	500

Отношение температуры заторможенного потока к статической температуре будет равно

.

Тогда отношение плотностей

.

Видно, число Маха является характеристикой сжимаемости рабочего тела:

При М→0 (с→0) →1.

При М→1 (с→а) →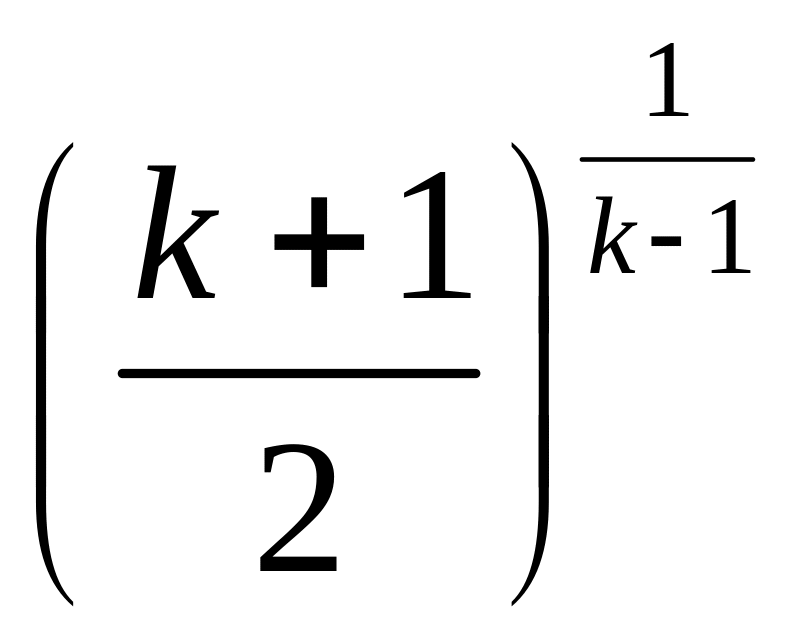 . Например, для воздуха при k=1,4 →1,577.

Из полученных выше уравнений можно определить максимальную скорость истечения, которая будет при Т=0:

, откуда .

Для воздуха с_max  44.8 . Например при Т^* = 300К, с_max = 776 м/с.

Увеличить с_max можно только увеличением Т^*(i^*).

Определим критическую скорость потока газа через параметры заторможенного потока. Для этого запишем уравнение сохранения энергии в виде

или т.к. .

Рассмотрим критический режим .

Тогда или =

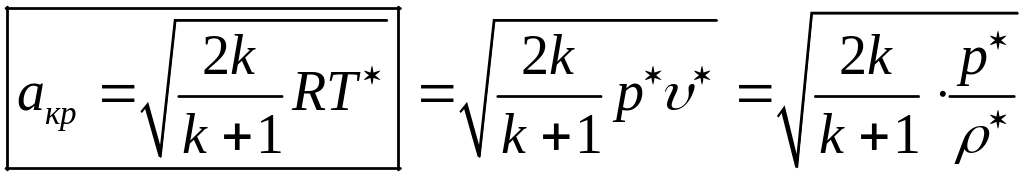=const.

Таким образом, критическая скорость, в отличие от скорости звука, постоянна вдоль потока т. к. . Поэтому она широко используется для расчета газовых течений.

Вопрос 5. Истечение газов с учетом трения

5.1 Изображение процесса в I – s и т - s диаграммах

Рассмотрим действительный процесс истечения газа из резервуара через сопло (конфузор) с учетом потерь на трение и вихреобразование, но без отвода теплоты в окружающую среду. Эти потери превращаются в теплоту, которая подводится к газу.

Изобразим изоэнтропный и действительный процессы расширения газа в конфузоре в Т-s и i-s диаграммах.

Из диаграмм видно, что энтальпия и статическая температура на выходе из сопла из-за подогрева газа в действительном процессе расширения будет больше, чем в изоэнтропном процессе (i₂>i_2s,Т₂>Т_2s).

Запишем уравнение движения газа (уравнение Бернулли) для изоэнтропного и действительного течений:

- изоэнтропное течение (процесс 1-2_s)

= =const=> и .

- действительное течение (процесс 1-2)

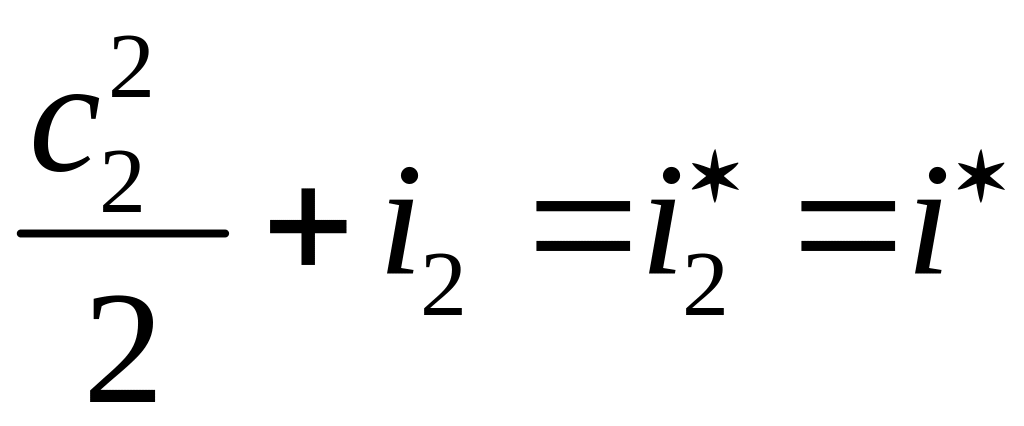= =const=> и .

Так как i₂>i_2s, то из формул и диаграмм видно, что кинетическая энергия и скорость потока газа на выходе из сопла в действительном процессе расширения будет меньше, чем в изоэнтропном процессе

и .

При этом удельная энтальпия заторможенного потока и температура заторможенного потока остаются равными как в действительном, так и в изоэнтропном процессе расширения и постоянными для любого сечения сопла (i^*=const, T^*=const).

Определим потерю кинетической энергии в действительном процессе расширения по сравнению с изоэнтропным процессом:

- кинетическая энергия на выходе из сопла в изоэнтропном процессе 1-2_s

- кинетическая энергия на выходе из сопла в действительном процессе 1-2

.

Тогда потеря кинетической энергии будет равна

Δh_к.э А2_s2D

Работа сил трения, которая в виде теплоты подведена к газу, эквивалентна площади под кривой процесса 1-2:

l_тр = q_тр = ψ₁₂ ≡ А12D > Δh_к.э.

Таким образом, в действительном процессе расширения газа потеря кинетической энергии меньше работы сил трения на величину площади 2_s12: Δh_к.э - l_тр ≡ 2_s12. Это объясняется тем, что часть работы сил трения в процессе расширения, после превращения в теплоту, вновь превращается в кинетическую энергию. Эта полезная часть работы сил трения называется возвращенным теплом q_{тр.возвр} ≡ 2_s12.

Сравним параметры в выходном сечении сопла при действительном и изоэнтропном процессах:

- параметры заторможенного потока

; ; ; т.к.

- статические параметры

; ; ( по условию); т.к. ; .