3.4. Момент сили відносно осі

Момент сили відносно осі — це скалярна величина, яка чисельно дорівнює моменту проекції цієї сили на площину, що перпендикулярна осі, відносно точки перетину осі з цією площиною.

Таким чином, для визначення момента сили відносно будь-якої осі (наприклад, осі , рис. 3.7, а) слід спроектувати силу на площину що перпендикулярна даній осі (рис. 3.7, б), визначити момент отриманої проекції відносно точки перетину осі з площиною (т. 0)

, (3.9)

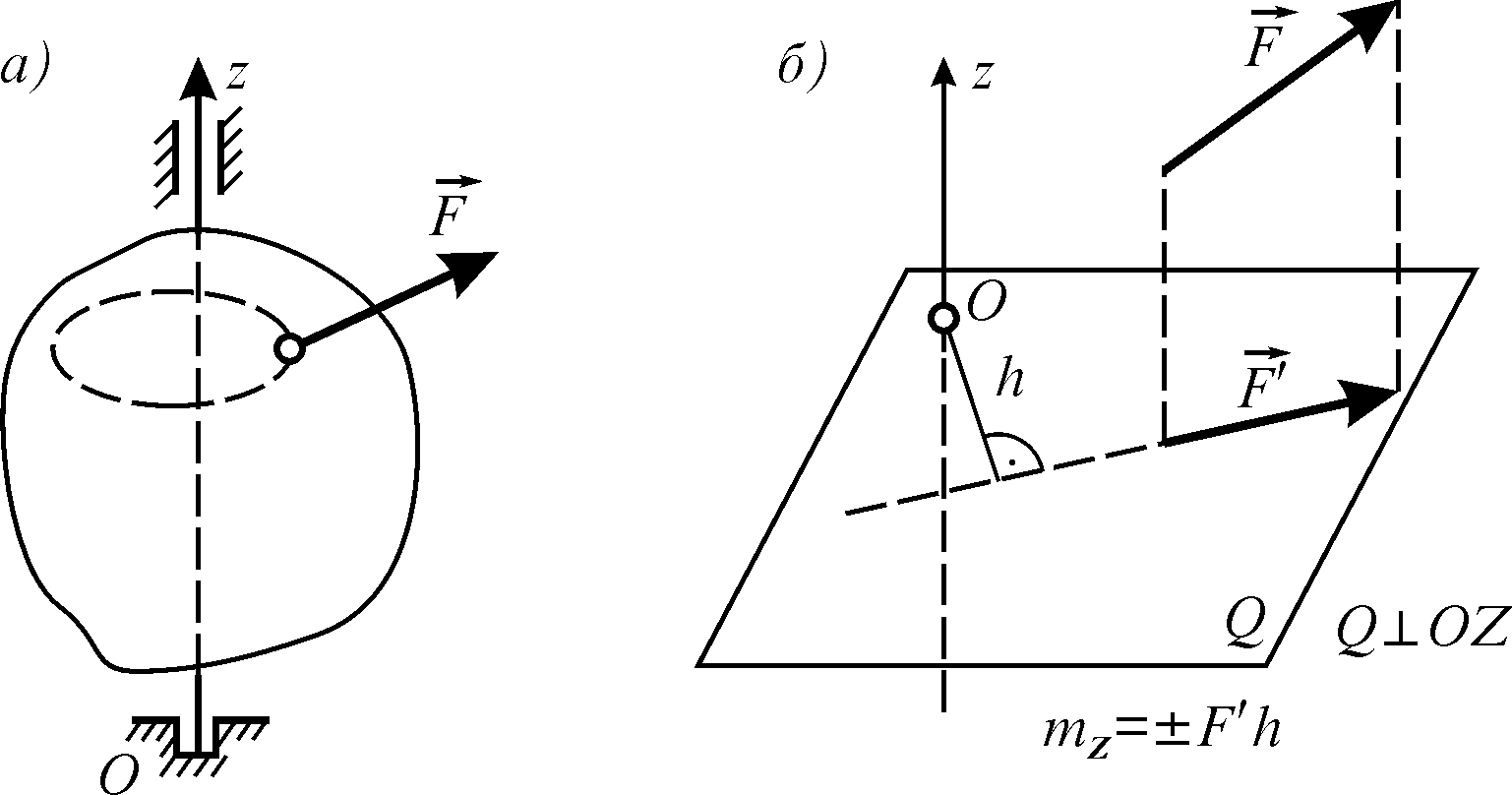
Рисунок 3.7

Момент сили відносно осі вважається додатнім, якщо при спостереженні з додатного напрямку осі видно, що сила прогне повернути тіло проти ходу годинникової стрілки (рис. 3.7, а), в супротивному випадку — від’ємним.

Момент сили відносно осі дорівняє нулю в двох випадках:

— проекція дорівнює нулю, тобто сила паралельна осі (рис. 3.8, а);

— плече дорівнює нулю, тобто лінія дії сили (проекції) перетинає вісь (рис. 3.8, б).

Часто при Знаходженні моменту сили відносно осі застосовують теорему Варіньона, згідно якій момент рівнодійної системи сил відносно осі дорівнює алгебраїчній сумі моментів складових відносно даної осі.

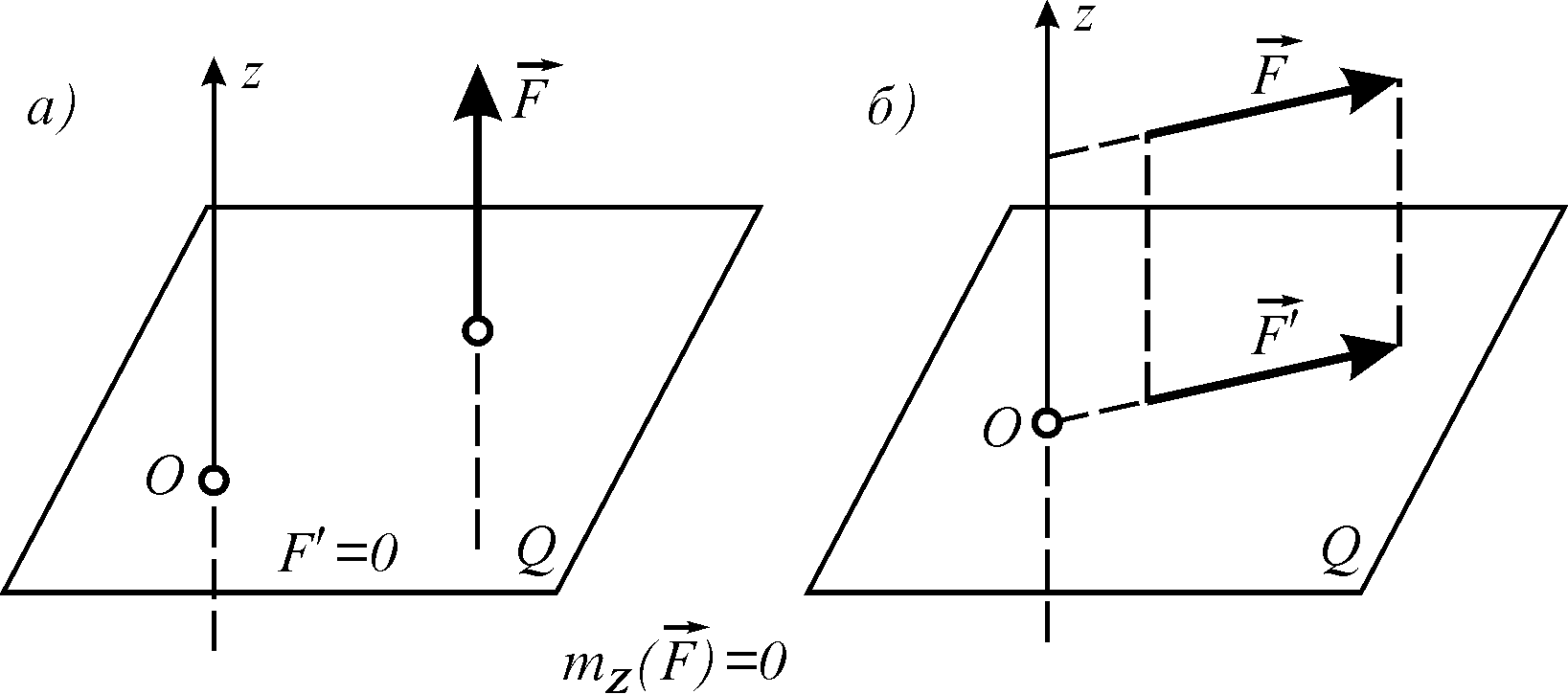
Рисунок 3.8

, (3.10)

Для застосування цієї теореми необхідно силу, момент якої потрібно визначити (рис. 3.9), розкласти на складові, і обчисли­ти момент сили як алгебраїчну суму моментів складових

(3.11)

де: — лінія дії сили перетинає вісь. У рівняннях (3.11) , оскільки складові , паралельні відповідним осям; внаслідок пе­ретину лінії дії даних складових з відповідними осями.

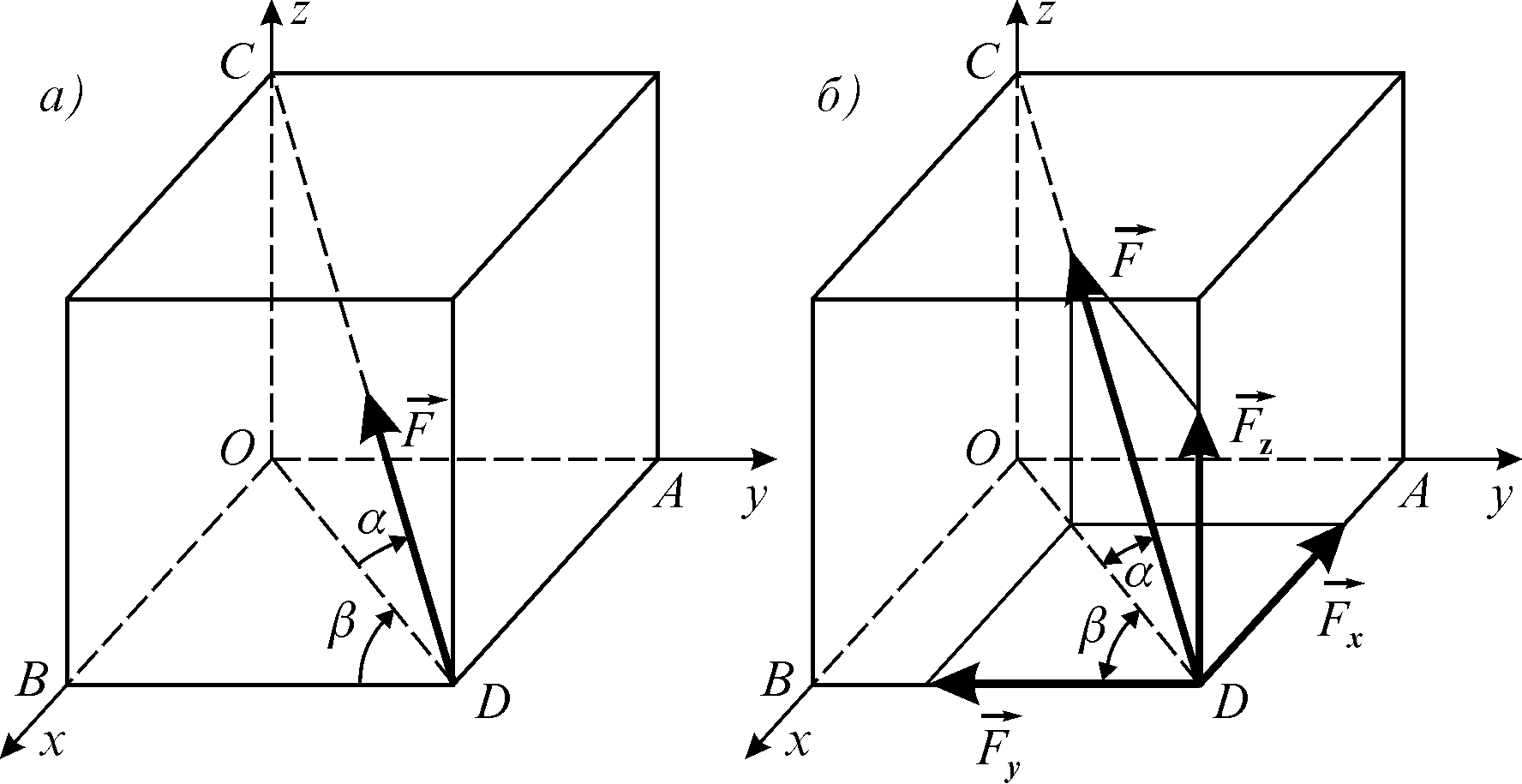
Рисунок 3.9

3.5. Пара сил та її момент

Пара сил — це система двох рівних за модулем, паралельних t протилежних за напрямком сил (рис. 3.10, а).

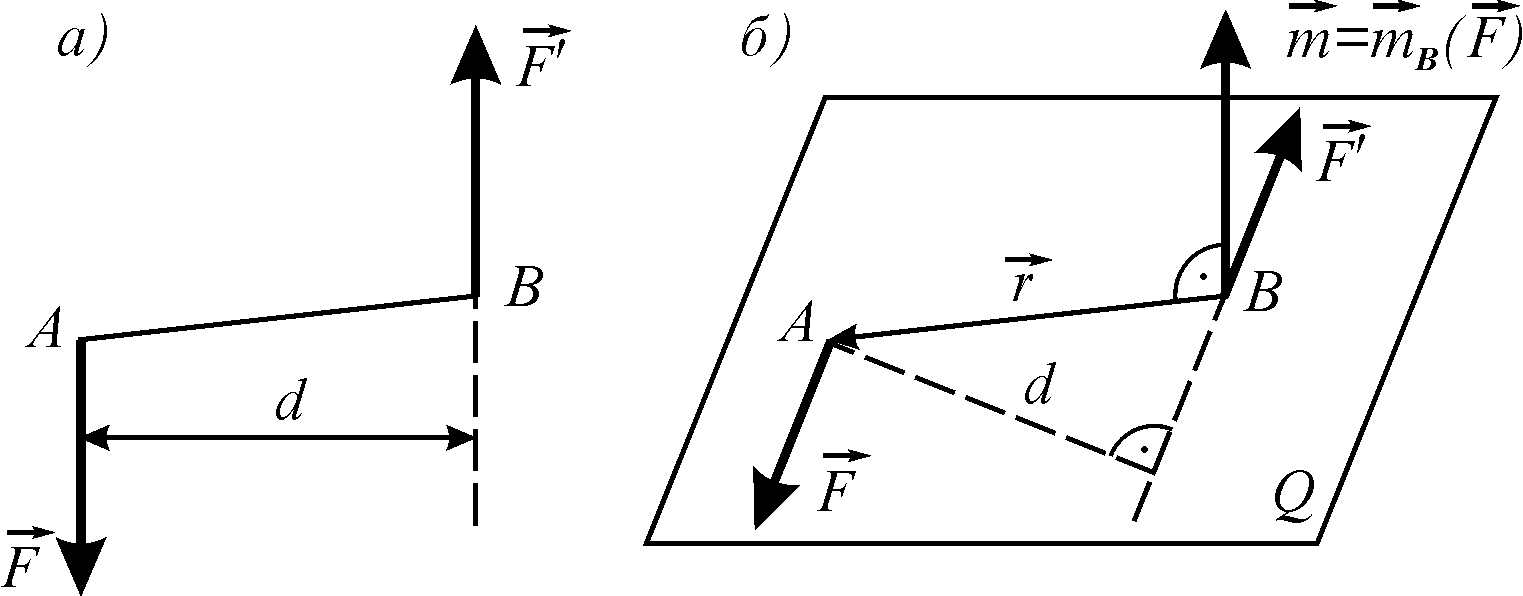
Рисунок 3.10

Основними характеристиками пари є:

1. Площина дії пари сил — це площина, в якій знаходяться лінії дії сил пари (рис. 3.10, 6 це площина ).

2. Плече пари ( ) — це найкоротша віддаль між лініями дії пари сил (рис. 3.10). Для визначення плеча пари необхідно з будь-якої точки лінії дії однієї сили пари опустити перпендику­ляр на лінію дії другої сили (рис. 3.10, б).

3. Момент пари сил — це вектор, який геометричне дорівнює моменту однієї сили .пари відносно точки прикладання другої сили

(3.11)

З даного визначення витікає, що:

— вектор моменту пари сил перпендикулярний до площини дії пари і спрямований в той бік, звідки обертання тіла парою сил видно проти ходу годинникової стрілки (рис. 3.10, 6);

— чисельно момент пари сил відносно будь-якої точки дорів­нює добутку модуля однієї сили пари на її плече

(3.12)

При цьому момент вважається додатнім (береться знак “+”), коли пара сил намагається повернути тіло в площині її дії проти ходу годинникової стрілки (рис. 3.11, а), і від’ємним (береться “-“) коли — за ходом годинникової стрілки (рис. 3.11, б).

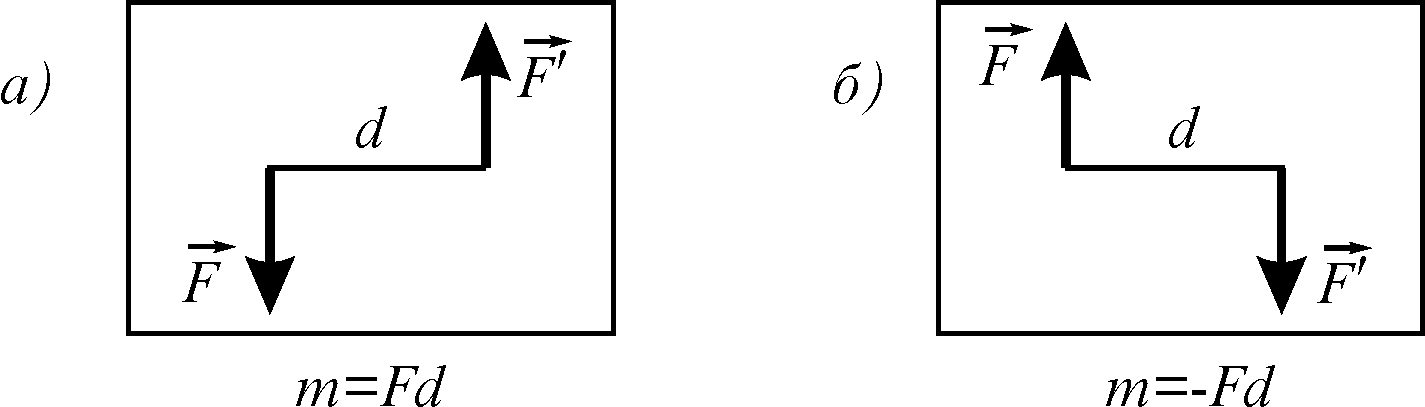
Рисунок 3.11

З теореми про еквівалентність пар сил (пари сил є еквіва­лентними, якщо їх моменти геометричне рівні) випливає, що дія пари сил на тверде тіло не зміниться, якщо:

пару сил перенести в будь-яке місце площини її дії;

пару сил перенести в будь-яку площину, яка паралельна площині її дії;

змінити плече пари, одночасно змінюючи величину її сил так, щоб незмінним зберігся її момент ( )

Можливі варіанти зображення дії пари сил на тверде тіло зображені на рис. 3.12.

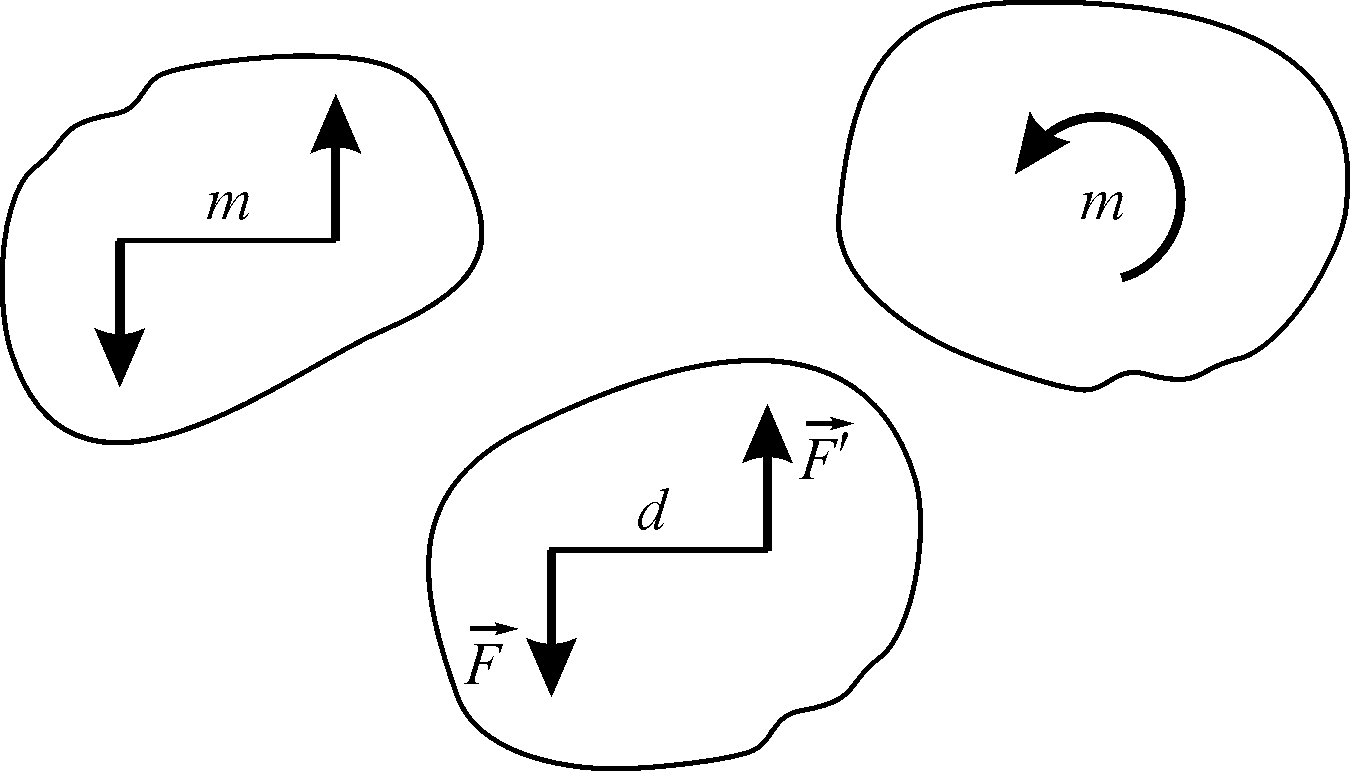
Рисунок 3.12