3.2. Проекція сили на вісь
Проекція сили на вісь — це скалярна величина, що чисел дорівнює довжині відрізку, що обмежений проекціями початку кінця вектора сили (рис. 3.1) на дану вісь.
Проекція сили на вісь береться зі знаком плюс або мінус залежно від напрямку відрізку, що визначає дану проекцію. Я його напрямок співпадає з додатнім напрямком осі (рис. 3.1, а), то проекція вважається додатною, в супротивному випадку проекція є від’ємною (рис. 3.1, б)
Позначимо
кут, що утворений вектором сили з додатнім
напрямком осі. Тоді (див. рис. 3.1) маємо
,
(3.1)
тобто проекція сили на вісь визначається добутком модуля сили на косинус кута між додатнім напрямком осі та вектором сили.
При обчисленні проекції сили на вісь можливі наступні випадки:
;
; 
;
(3.2)
;
;
; 
;
(3.3)
;
; 
;
(3.4)
Практично при обчисленні проекції вектора сили на вісь модуль вектора сили множать на косинус гострого кута між вектором сили та віссю проекції. Знак проекції визначають безпосередньо за кресленням: знак плюс, якщо кут між вектором сили та додатнім напрямком осі проекції гострий (рис. 3.1, а та 3.2, а), і мінус якщо цей кут — тупий (рис. 3.1, б та 3.2, в).
Аналогічно визначаються проекції сили на інші координатні осі.
Іноді
при обчисленні проекції сили на вісь
використовують спосіб подвійного
проектування. Цей спосіб застосовують
у випадку, коли кут між напрямком сили
та осі попередньо невідомий і його важко
визначити.
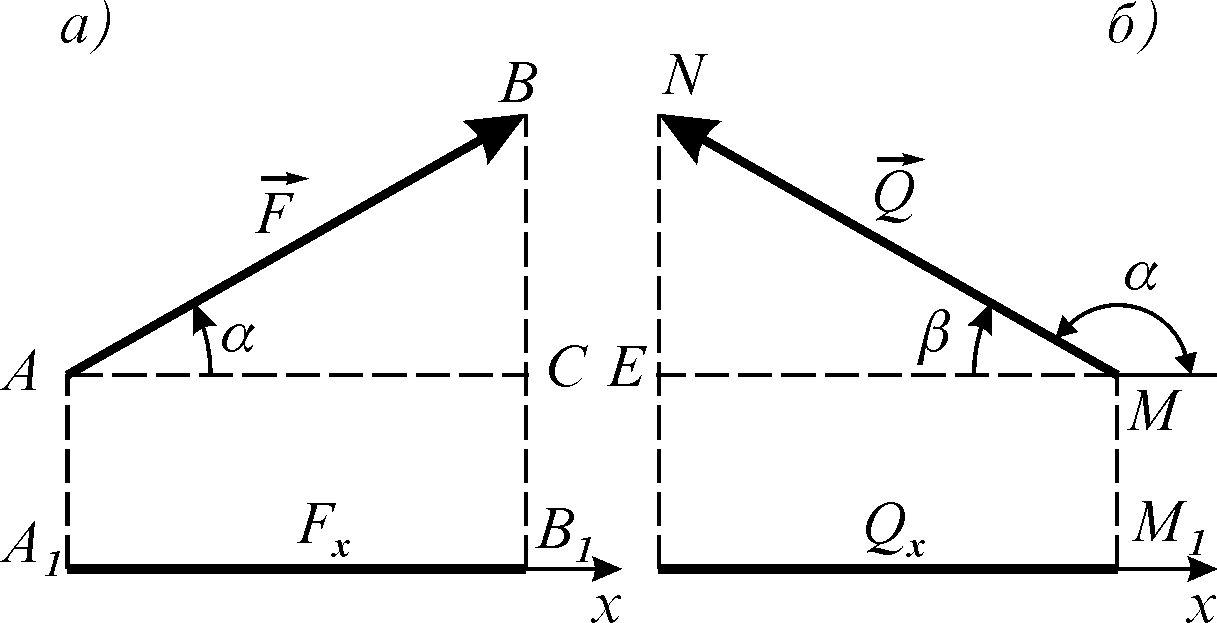
Рисунок 3.1
Рисунок 3.2
Наприклад,
при визначенні проекцій вектора сили
на осі
та
(рис. 3.3)
проектуємо на площину
й наступним повторним проектуванням
знаходимо відповідні проекції:
|
|
Рисунок 3.3
; (3.5)
. (3.6)
3.3. Момент сили відносно точки
Момент
сили відносно точки 0
— це вектор
,
що прикладений у точці 0 перпендикулярно
до площини, що проходить через точку 0
та вектор сили
,
який спрямований у той бік, звідки
обертання тіла силою видно проти ходу
годинникової стрілки (рис. 3.4). Чисельно
момент сили відносно точки дорівнює
добутку модуля сили на її плече,
взятому з певним знаком
,
(3.7)
Плече сили — це довжина перпендикуляру, опушеного з точки 0 на лінію дії сили ( рис. 3.4)
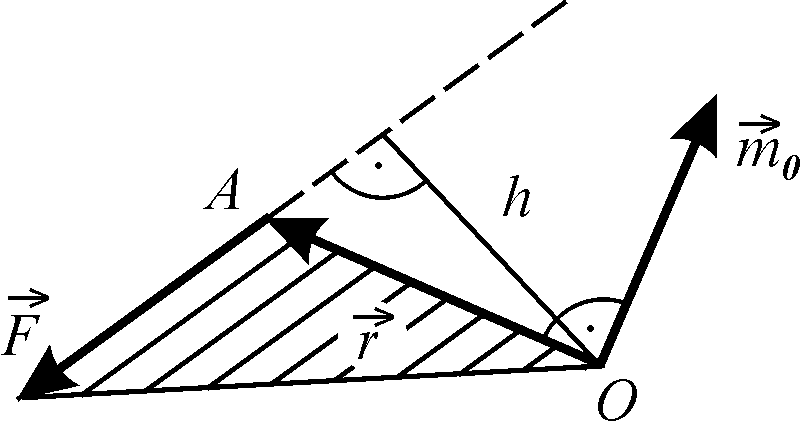
Рисунок 3.4
Якщо сила прагне обертати тіло навколо даної точки 0 проти годинникової стрілки (рис. 3.5, а), то момент сили відносно цієї точки вважається додатнім, а в супротивному випадку — від’ємним (рис. 3.5, б). Якщо лінія дії сили проходить через дану точку 0 (рис. 3.5, в), то момент сили відносно цієї точки дорівнює нулю.
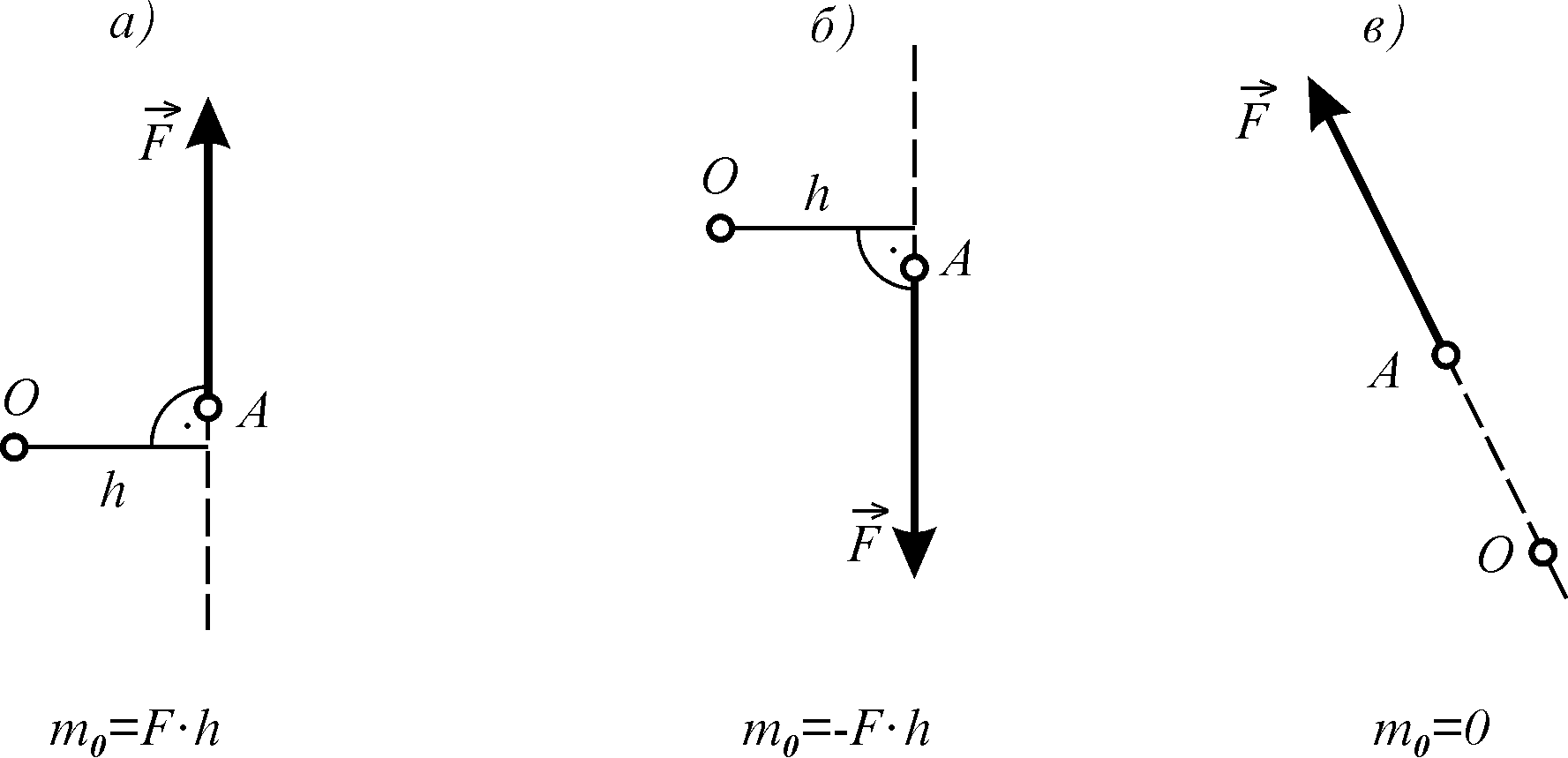
Рисунок 3.5
Рекомендація
У випадках, коли обчислення моменту сили утруднене через складність визначення плеча сили, рекомендується використовувати теорему Варіньона, згідно якій момент рівнодійної системи відносно будь-якої точки дорівнює геометричній сумі моментів усіх сил системи відносно тієї ж точки
.
(3.7)
Для плоскої системи сил рівняння (3.7) можна записати у вигляді
,
(3.8)
тобто момент рівнодійної плоскої системи сил відносно будь-якої точки дорівнює алгебраїчній сумі моментів всіх сил системи відносно даної точки.
При визначенні моменту сили відносно будь-якої точки 0 за допомогою теореми Варіньона дану силу розкладають на складові, моменти яких відносно даної точки 0 легко визначаються. Момент же сили відносно точки 0 обчислюють як алгебраїчну суму моментів складових (рис. 3.6):
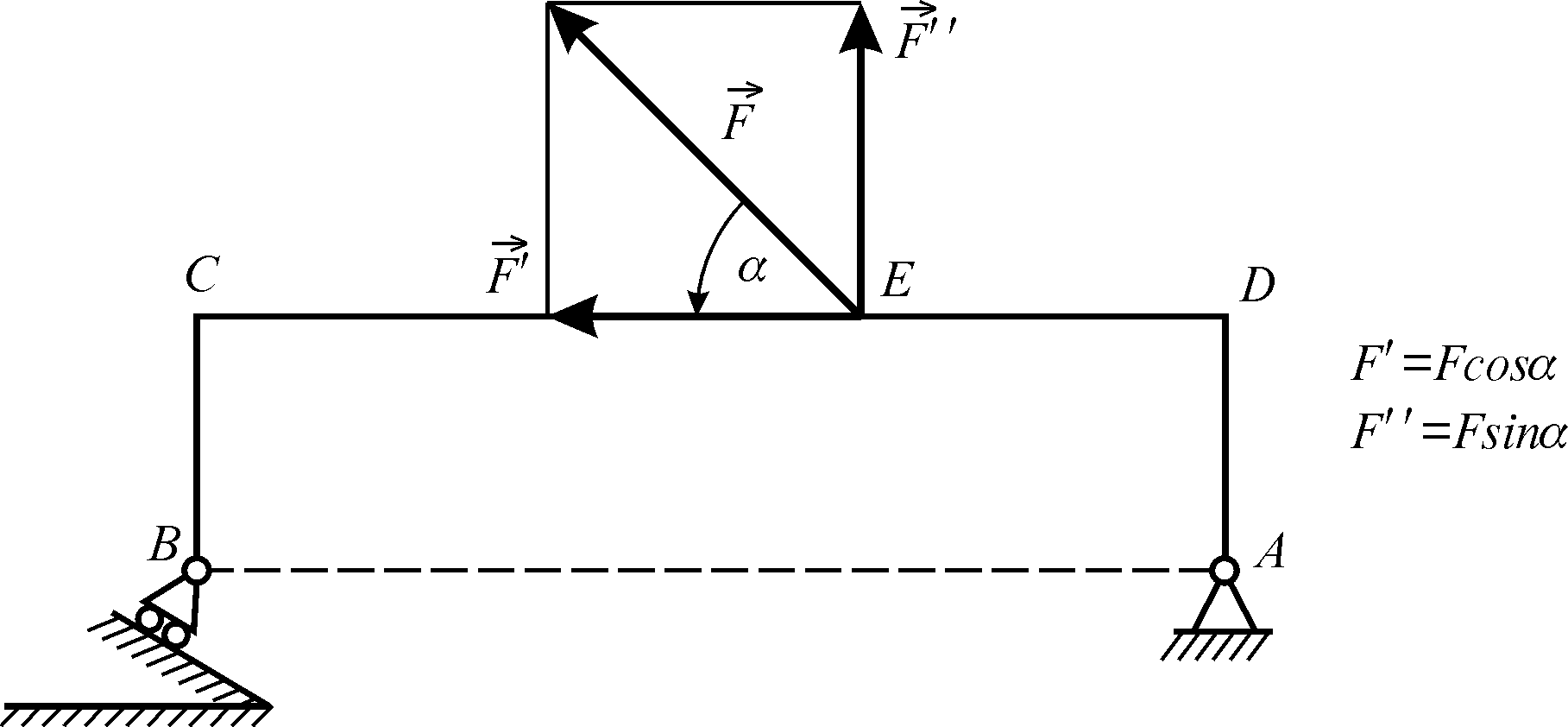
Рисунок 3.6