1.7 Визначення прискорення вантажу за рівнянням Лагранжа іі роду

Рівняння Лагранжа ІІ роду має вигляд

(1.77)

де – кінетична енергія системи; – узагальнена координата; – узагальнена сила; – узагальнена швидкість; – число степеней кількості системи (число узагальнених координат).

Примітка:

1. Число рівнянь Лагранжа рівне числу незалежних узагальнених координат даної системи.

2. Невідомі реакції ідеальних в’язей, накладених на систему, в ці рівняння не входять.

3. Кінетична енергія механічної системи визначається, як функція узагальнених координат, узагальнених швидкостей і часу.

4. Кожній узагальненій координаті відповідає своя узагальнена сила, яка визначається за формулою

. (1.78)

Розглянемо задану механічну системи (рис. 1.10).

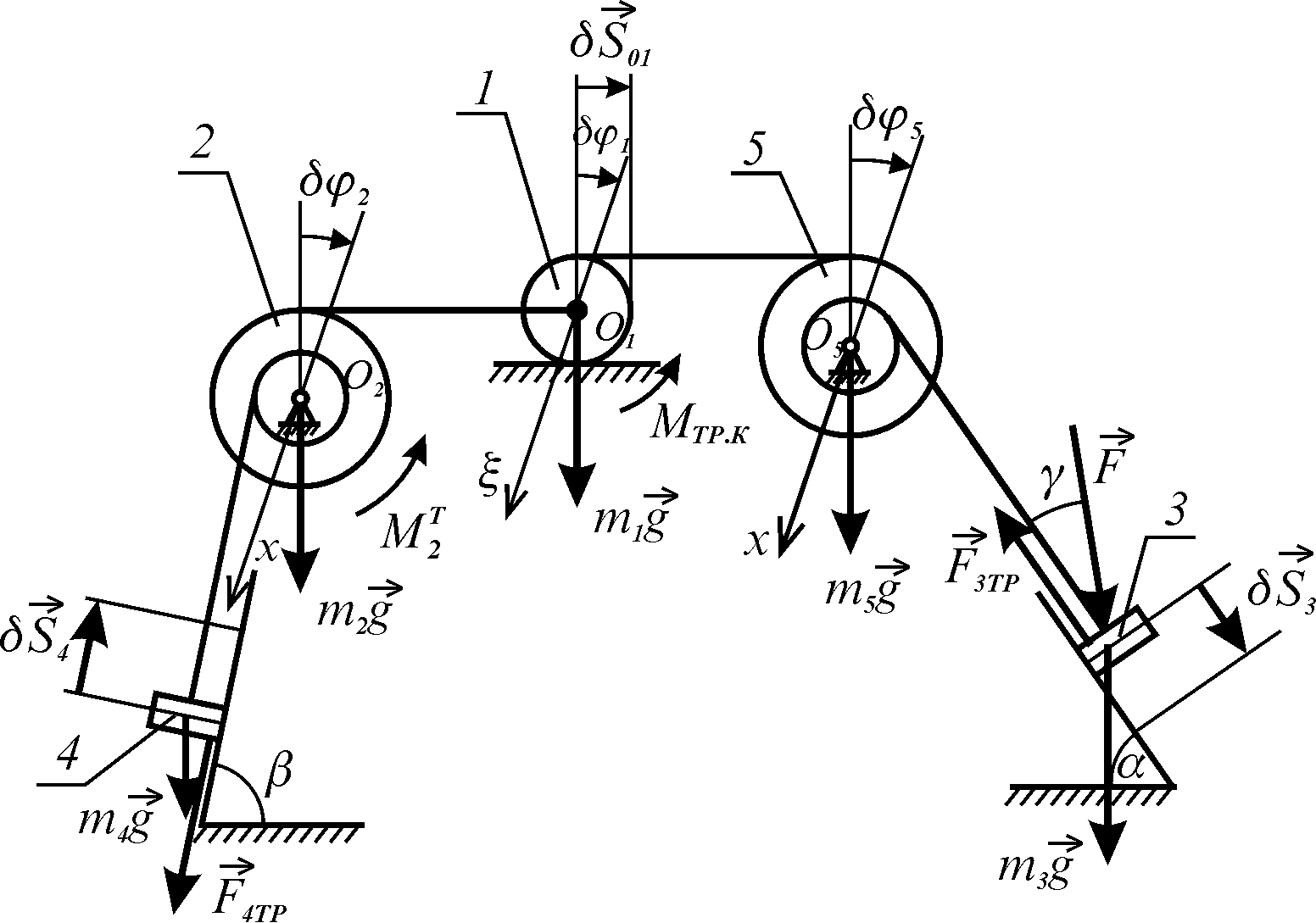
Рисунок 1.10

Ця система має одну ступінь вільності, а тому її положення може бути визначено однією узагальненою координатою За узагальнену координату приймемо переміщення ланки 3, тоді узагальнена швидкість буде рівна .

На основі (1.77) складаємо рівняння Лагранжа

. (1.79)

1. Кінетичну енергію системи визначимо як функцію узагальненої швидкості . Скористаємося виразом (1..59)

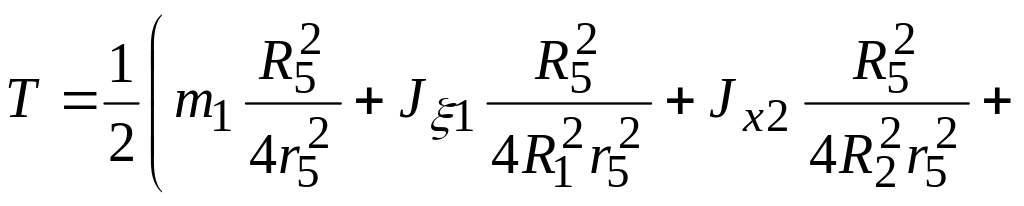
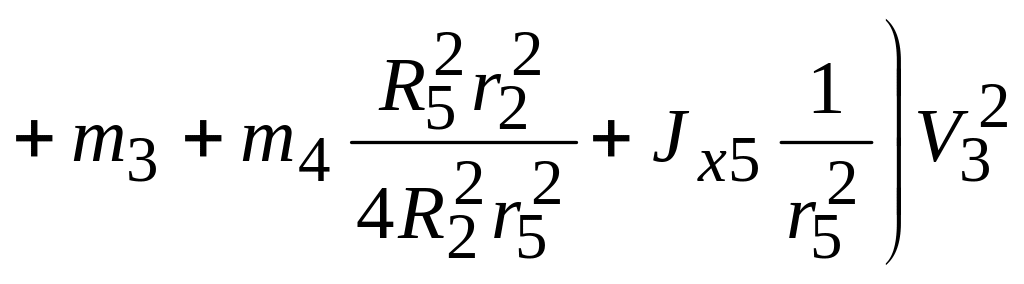. (1.80)

2. Прикладемо до системи всі задані сили

і моменти . Для обчислення узагальненої сили , яка відповідає узагальненій координаті , надамо цій координаті приріст і складемо суму елементарних робіт всіх заданих сил на отриманому переміщенні системи:

. (1.81)

На основі співвідношень (1.8)

.(1.82)

(1.81) прийме вигляд

. (1.83)

Узагальнена сила на основі (1.78) рівна

. (1.84)

3. Отримані значення підставляємо в (1.79). Для цього попередньо знайдемо відповідні похідні:

;

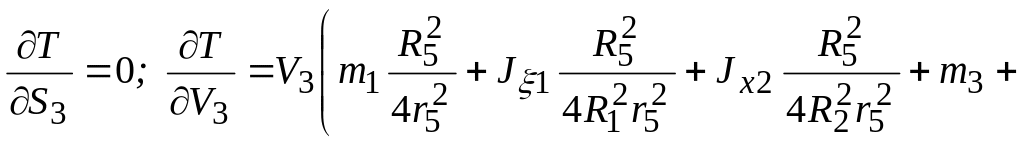
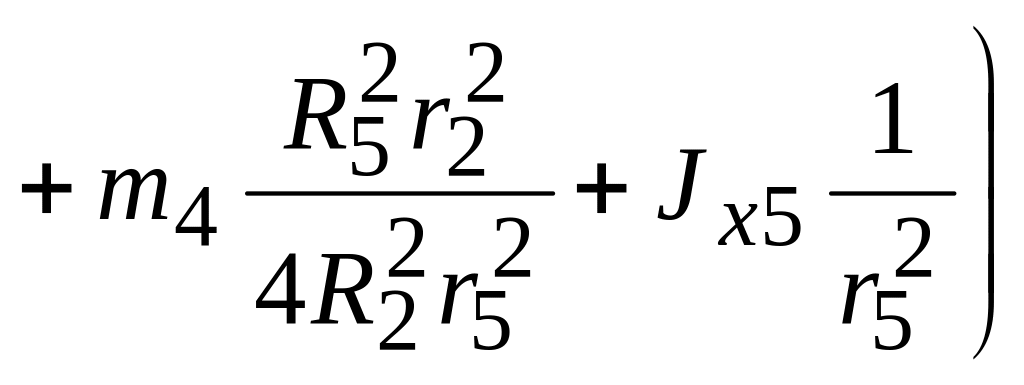(1.85)

.

4. Підставляючи (1.84) і (1.85) в рівняння (1.79) і виконуючи певні перетворення, отримаємо

, (1.86)

що відповідає виразу, отриманому раніше.

1.8 Числовий розрахунок прискорення вантажу

Для отримання числового значення визначимо:

1. Силу тертя вантажу 3 з площиною нахиленою до горизонту під кутом .

(н). (1.87)

2. Сила тертя вантажу 4 з площиною нахиленою до горизонту під кутом рівна

(н). (1.88)

3. Момент тертя кочення катка 1 рівний

(Нм). (1.89)

4. Момент інерції однорідного циліндричного катка, визначається формулою

(кгм²), (1.90)

де – маса катка; – вісь, яка проходить через центр мас перпендикулярно площині рисунка; – радіус катка.

5. Момент інерції шківа 2, маса якого рівно розподілена вздовж його ободу, рівний

(кгм²), (1.91)

де – радіус обода шківа.

6. Момент інерції шківа 5, радіус інерції якого рівний м

(кгм²). (1.92)

7. Підставимо значення мас ланок механізму, радіусів шківів і катка, моменту опору кутів , а також (1.5), (1.92), (1.91), (1.90), (1.89), (1.88) і (1.87) і (1.86), отримаємо:

(1.93)

(м/с²)

Відповідь: Прискорення вантажу 3 рівне м/с².