1.4 Визначення прискорення вантажу за теоремою про зміну моменту кількості руху механічної системи

Зміна кінематичного моменту системи відносно осі виражається рівнянням

, (1.21)

де – кінетичний момент системи відносно осі; – головний момент всіх зовнішніх сил, які діють на систему відносно тої ж осі.

Для вирішення задачі даним методом необхідно:

1. Знайти кінетичний момент системи відносно осей обертання, як суму моментів кількості руху тіл, які входять в цю систему відносно даної осі.

2. Прикласти всі зовнішні сили, діючі на систему.

3. Знайти суму моментів всіх зовнішніх сил відносно осі обертання, яка розглядається.

4. Отримані результати підставити в рівняння (1.21) і розв’язати це рівняння.

Перейдемо до розв’язку задачі.

1. Спочатку розглянемо систему тіл (вантаж 3 і шків 5, рис. 1.5) які рухаються відносно осі . Кінетичний момент цієї системи відносно осі знайдемо як суму моментів кількості руху вантажу і шківа 5

. (1.22)

Рисунок 1.5

Момент кількості руху вантажу 3 відносно осі

, (1.23)

де – швидкість вантажу 3.

Момент кількості руху ланки 5 відносно осі

, (1.24)

де – момент інерції ланки 5 відносно осі ; – кутова швидкість ланки 5.

Враховуючи (1.23) і (1.24) вираз (1.22) приймає вигляд

. (1.25)

Прикладемо всі зовнішні силові фактори, діючі на цю систему (рис. 1.5).

Це будуть

– сили ваги ланок;

– сили тертя вантажу в похилу площину;

– нормальна реакція похилої площини;

– реакція підшипника ланки 5;

– сила натягу нитки, яка з’єднує шків 5 і каток 1;

– задана змінна сила, діюча на ланку 3.

Знаходимо суму моментів всіх цих сил відносно осі .

Отримаємо

.(1.26)

Примітка.

Моменту приписуємо знак “+”, якщо він напрямлений в сторону обертання ланки 5, і знак “-”, якщо він напрямлений в протилежну сторону.

Підставляючи (1.26) і (1.25) в рівняння (1.21), попередньо врахувавши співвідношення (1.6)

, (1.27)

отримаємо

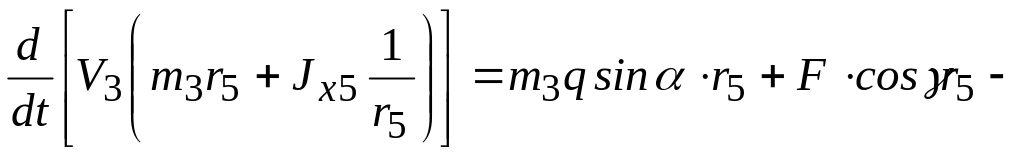
. (1.28)

Звідки

. (1.29)

2. Розглянемо ланки 4 і 2 (рис. 1.6), які рухаються відносно осі . Кінетичний момент цієї системи відносно осі знайдемо як суму моментів кількості руху вантажу 4 і шківа 2

. (1.30)

Рисунок 1.6

Момент кількості руху вантажу 4 відносно осі

, (1.31)

де – швидкість ланки 4.

Момент кількості руху шківа 2 відносно осі

, (1.32)

де – момент інерції ланки 2 відносно осі ; – кутова швидкість ланки 2.

Враховуючи (1.31) і (1.32) вираз (1.30) буде мати вигляд

, (1.33)

де на основі (1.6)

. (1.34)

Прикладемо всі зовнішні силові фактори, які діють на ланки 4 і 2 (рис. 1.6):

– сили ваги ланок 4 і 2;

– сила тертя вантажу 4 по похилій площині;

– реакція підшипника ланки 2;

– сила натягу нитки, яка з’єднує шків 2 і каток 1.

Знаходимо суму моментів всіх цих сил відносно осі .Отримаємо

. (1.35)

Підставимо (1.35) і (1.33), враховуючи (1.34) в (1.21), отримаємо

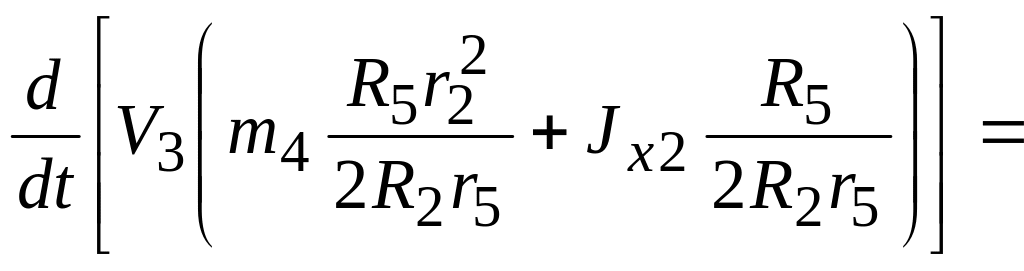
. (1.36)

Звідки

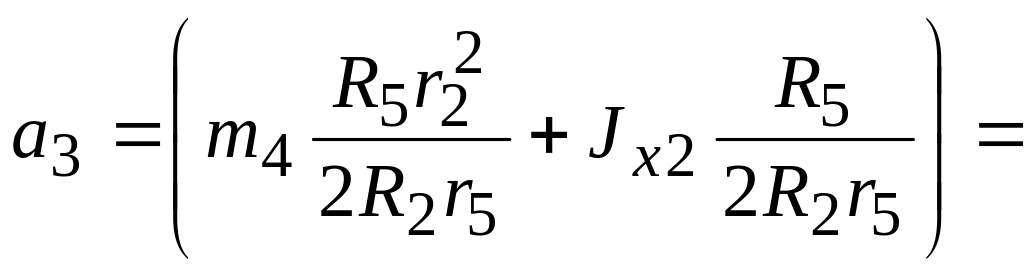
. (1.37)

3. Розглянемо каток 1, який здійснює плоскопаралельний рух (рис. 1.7).

Рисунок 1.7

В нашому випадку каток 1 поступально рухається по горизонтальній площині з швидкістю і обертається навколо миттєвої осі з кутовою швидкістю .

Кінетичний момент ланки 1 відносно миттєвої осі обертання знаходимо як суму моментів кількості руху в поступальному і обертальному його рухах.

. (1.38)

Момент кількості руху катка 1 відносно осі в поступальному русі

. (1.39)

Момент кількості руху відносно осі в його обертальному русі

, (1.40)

де – момент інерції катка відносно осі , яка проходить через центр мас .

Підставляючи (1.39) і (1.40) в (1.38) отримаємо

, (1.41)

де на основі (1.6), маємо:

. (1.42)

Прикладемо всі зовнішні силові фактори, діючі на ланку 1

– сила ваги катка;

– сили натягу ниток, які з’єднують каток 1 з шківами 5 і 2;

– момент тертя кочення;

– сила щеплення катка з площиною.

Знаходимо суму моментів всіх цих силових факторів відносно миттєвої осі обертання .

Отримаємо

. (1.43)

Підставимо (1.43) і (1.41), враховуючи (1.42) в (1.21), отримаємо

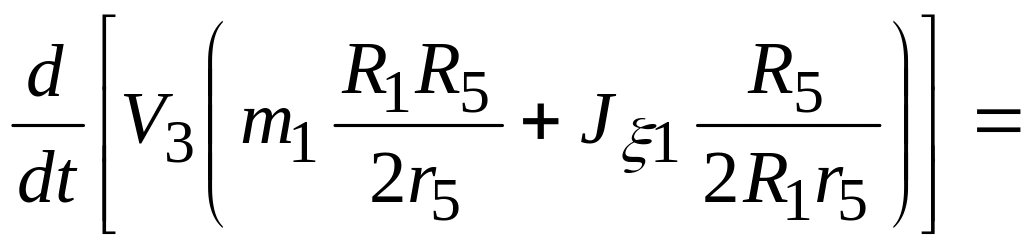
. (1.44)

Звідки

. (1.45)

4. Розв’язуючи систему рівнянь (1.29), (1.37) і (1.45) і враховуючи, що і , отримаємо

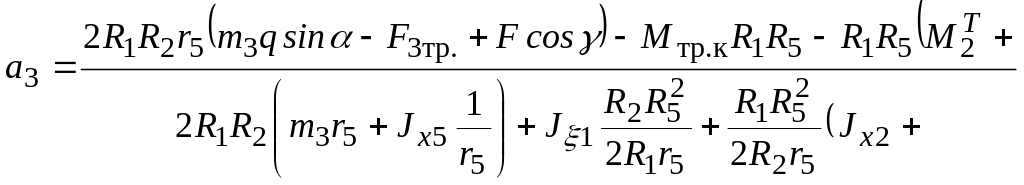
(1.46)

що відповідає виразу, отриманому раніше.