Задача д11

До горизонтального вала, що закріплений у підшипниках А та В жорстко прикріплені: в точці — однорідний суцільний диск радіуса м й масою кг, площина котрого перпендикулярна до осі вала, а центр ваги зміщений від осі вала на відстань ; в точці — тонкий прямолінійний стрижень довжиною м й масою кг, що утворює з віссю вала кут До вала прикладений обертовий момент М, як вказано на рис. Д 11.

В момент часу с визначити реакції підшипників А та В; обчислити у відсотках долю їхніх динамічних складових, якщо у вказаний момент часу відрізок та стрижень знаходиться в координатних площинах, що вказані в табл. Д 11а. Необхідно для розв’язання дані наведені в табл. Д 11а та Д 11б.

Таблиця Д 11а Таблиця Д 11б

Варіант	Нм	м	Коорд. площини, в яких знаходиться			Варіант	м	м	м	град
1	8	0,05				1	0,2	0,5	0,3	30
2	10	0,10				2	0,3	0,2	0,5	45
3	12	0,15				3	0,5	0,3	0,2	60
4		0,20				4	0,2	0,6	0,2	90
5		0,25				5	0,6	0,2	0,2	120
6	14	0,30				6	0,3	0,3	0,4	135
7		0,50				7	0,4	0,2	0,4	150
8	5	0,40				8	0,2	0,7	0,1	30
9	9	0,20				9	0,3	0,4	0,3	60
0	7	0,00				0	0,3	0,5	0,2	120

У вказаний момент часу вал має кутову швидкість с^-1.

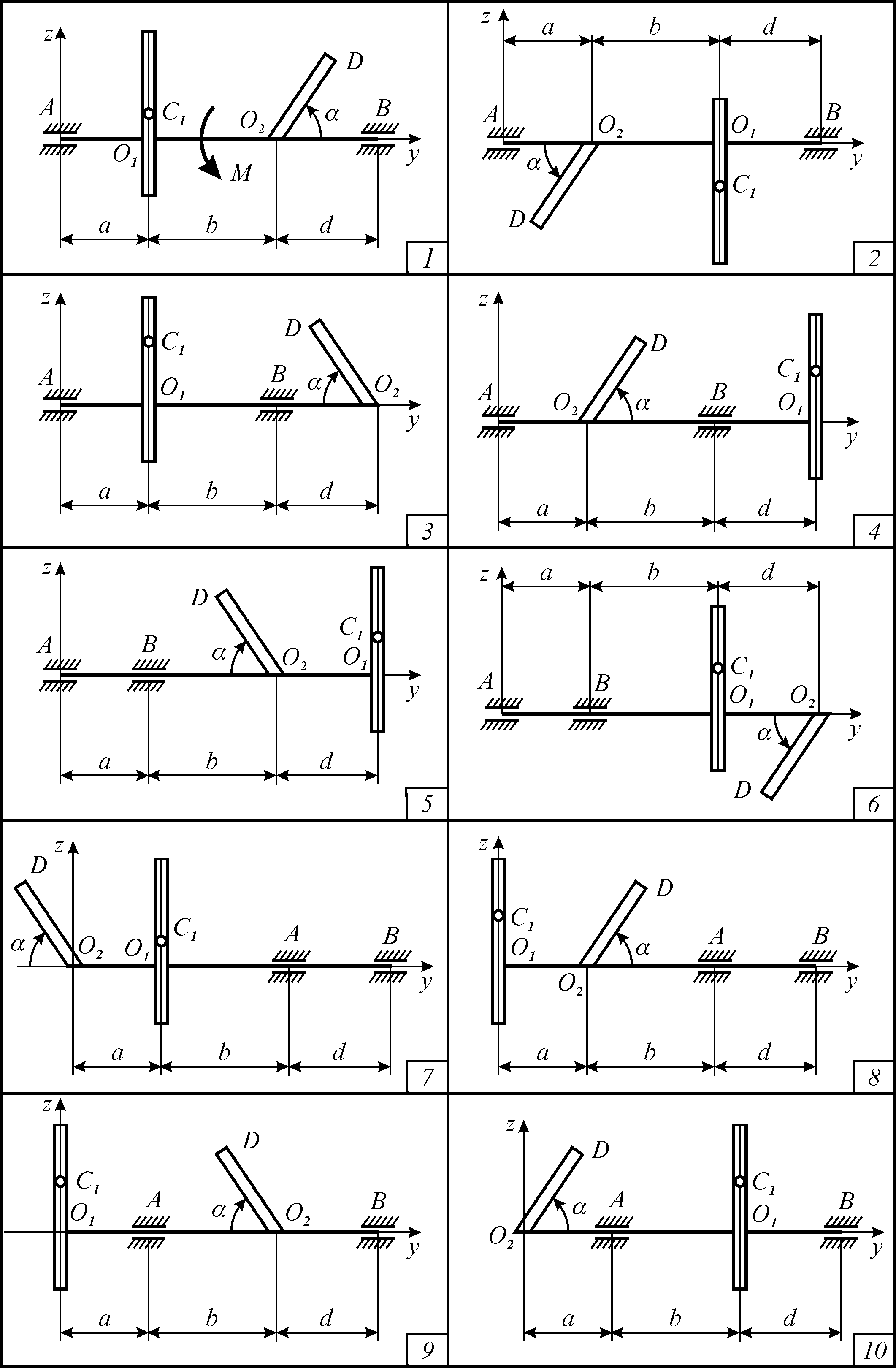
Рисунок Д11

Задача д12

На механізм, що розташований у горизонтальній площині, діють, як показано на рис. Д12, пара сил з моментом М та дві сили та . Довжини стрижнів дорівнюють

м; м. Довжини інших стрижнів вибрати самостійно. Точка К знаходиться посередині стрижня АВ.

Згідно заданим К та визначити величину й напрямок сили , якщо механізм перебуває в рівновазі в положенні, що визначається кутами . Значення всіх заданих величин подані в табл. Д 12а та Д 12б.

Таблиця Д 12а Таблиця Д 12б

Варіант	Нм					Варіант	Н
		град						град
1	10	90	150	30		1	100	30	60
2	12	50	120	60		2	120	45	60
3	14	45	135	45		3	140	60	45
4	18	30	90	60		4	160	90	30
5	20	0	60	120		5	180	120	60
6	19	120	45	135		6	200	135	30
7	17	135	30	150		7	220	150	45
8	15	150	120	60		8	240	30	30
9	13	180	150	30		9	260	45	60
0	11	30	135	45		0	280	60	30

Примітка: побудову креслення починати зі стрижня положення котрого визначається кутом .

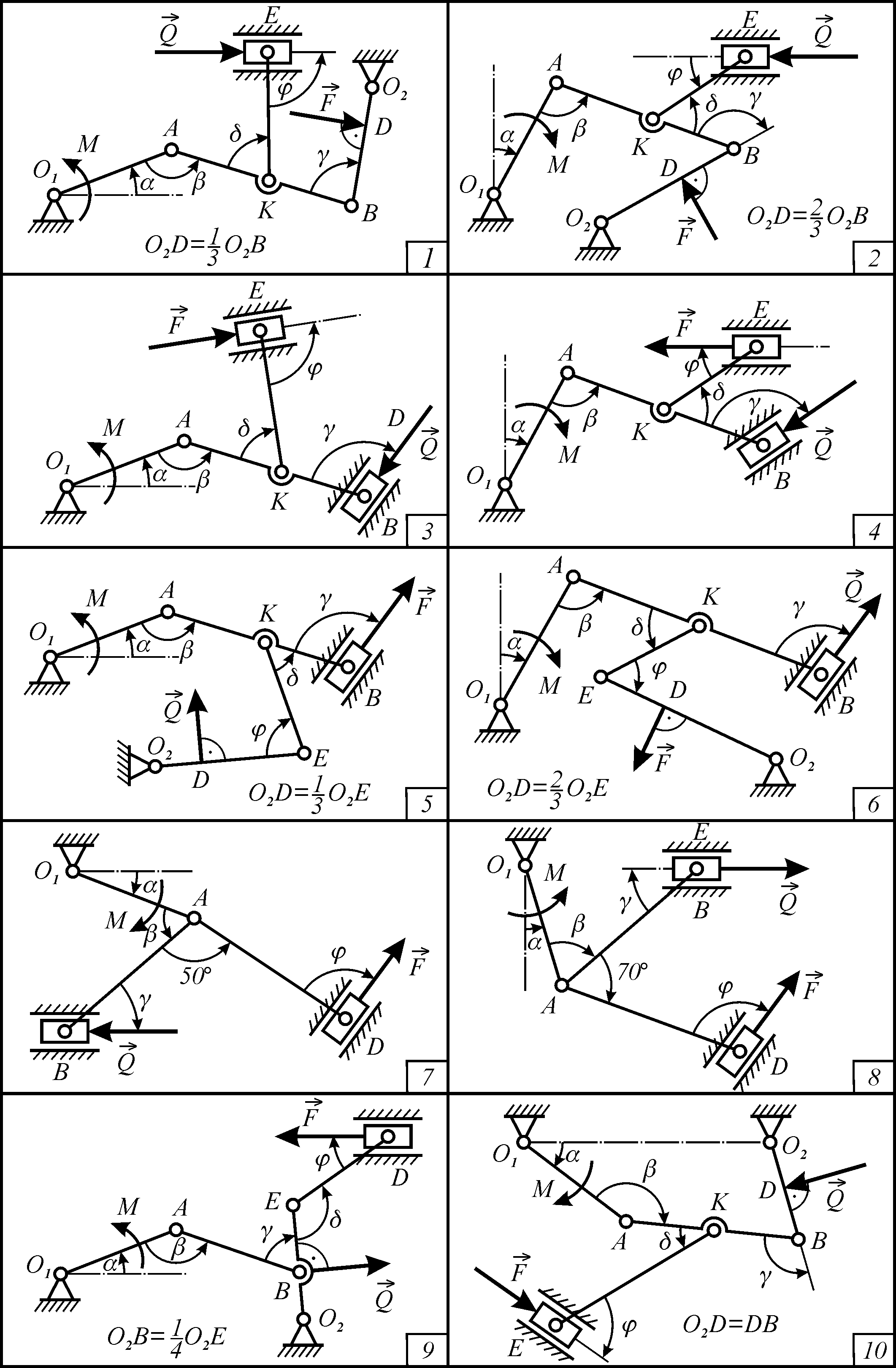
Рисунок Д12

ЗАДАЧА Д13

Застосовуючи принцип можливих переміщень, визначити реакції зовнішніх опор складної конструкції, котра задана у задачі С4. Необхідні для розв’язання дані вибрати з табл. С 4а та С 4б.

ЗАДАЧА Д14

Застосовуючи загальне рівняння динаміки, визначити кутове прискорення шківа 2 механізму, що заданий у задачі Д10. Необхідні для розв’язання дані вибрати з табл. Д 10а та Д 10б.

ЗАДАЧА Д15

Складаючи рівняння Лагранжа другого роду, визначити кутове прискорення шківа 2 механізму, що заданий у задачі Д10. Необхідні для розв’язання дані вибрати з табл. Д 10а та Д 10б.

ЗАДАЧА Д 16-1

Скласти диференційні рівняння руху механічної системи, що складається з точки А масою і точки В масою котрі з’єднані невагомим стрижнем довжини . Точка А рухається гладкою циліндричною поверхнею радіуса (рис. Д 16-1).

ЗАДАЧА Д 16-2

Скласти диференційні рівняння руху механічної системи, що складається з тіла 1 масою і точки 2 масою . Точка й тіло з’єднані невагомим стрижнем. Саме тіло приєднано до вертикальної стіни пружини, коефіцієнт жорсткості якої С (рис. Д 16-2). Тертям знехтувати. Довжина стрижня .

ЗАДАЧА Д 16-3

Дошка АВ масою рухається похилою площиною, що складає з горизонтом кут . нею може рухатися без ковзання однорідний суцільний циліндр масою (рис. Д 16-3). Скласти диференційні рівняння руху системи. Всіма опорами знехтувати.

ЗАДАЧА Д 16-4

На гладкій горизонтальній площині розміщена трикутна призма масою . Гранню призми котиться без ковзання однорідний круглий циліндр масою . Скласти диференційні рівняння руху системи, якщо до призми прикладена сила . Всіма опорами знехтувати (рис. Д 16-4).

ЗАДАЧА Д 16-5

Механічна система, що складається з тіла А масою та суцільного однорідного циліндра масою , знаходиться на гладкій площині, котра складає з горизонтом кут (рис. Д 16-5). До тіла прикріплена тонка нитка, що намотана на циліндр, який, розмотуючи нитку, скочується площиною. Скласти диференційні рівняння руху системи, якщо до тіла А прикладена сила . Всіма опорами знехтувати.

ЗАДАЧА Д 16-6

Система складається з тонкого однорідного стрижня 1 масою , на одному кінці якого є горизонтальна вісь обертання А, а на другому — за допомогою пружини з коефіцієнтом жорсткості прикріплений вантаж масою . Стрижень утримується у вертикальній площині пружини з коефіцієнтом жорсткості . Скласти диференційні рівняння руху системи.

ЗАДАЧА Д 16-7

Однорідний суцільний циліндр масою і радіуса , падаючи під дією сили ваги, призводить до руху за допомогою тонкої невагомої нитки блок 2 радіуса ; маса котрого рівномірно розподілена уздовж його ободу (рис. Д 16-7). Нехтуючи всіма опорами, скласти диференційні рівняння руху системи.

ЗАДАЧА Д 16-8

Однорідний суцільний циліндр А масою та радіуса , рухається гладкою похилою площиною, що складає з горизонталлю кут . Циліндр обмотано тонкою невагомою ниткою, що перекинута через невагомий блок С й прикріплено до вантажу В масою . Скласти диференційні рівняння руху системи (рис. Д 16-8).

ЗАДАЧА Д 16-9

Матеріальна точка А масою рухається уздовж тонкого однорідного кільця радіуса та масою , котра обертається навколо вертикальної осі під дією моменту М (рис. Д 16-9). Скласти диференційні рівняння руху системи.

ЗАДАЧА Д 16-0

Скласти диференційні рівняння руху механічної системи, що складається з однорідного суцільного циліндра масою , котрий скочується без ковзання похилою площиною, що утворює кут з горизонтом, й тонкого прямолінійного стрижня довжиною 0,6 м та масою . Стрижень здійснює коливання навколо осі, що проходить через центр циліндра перпендикулярно до площини рисунка (рис. Д 16-0).

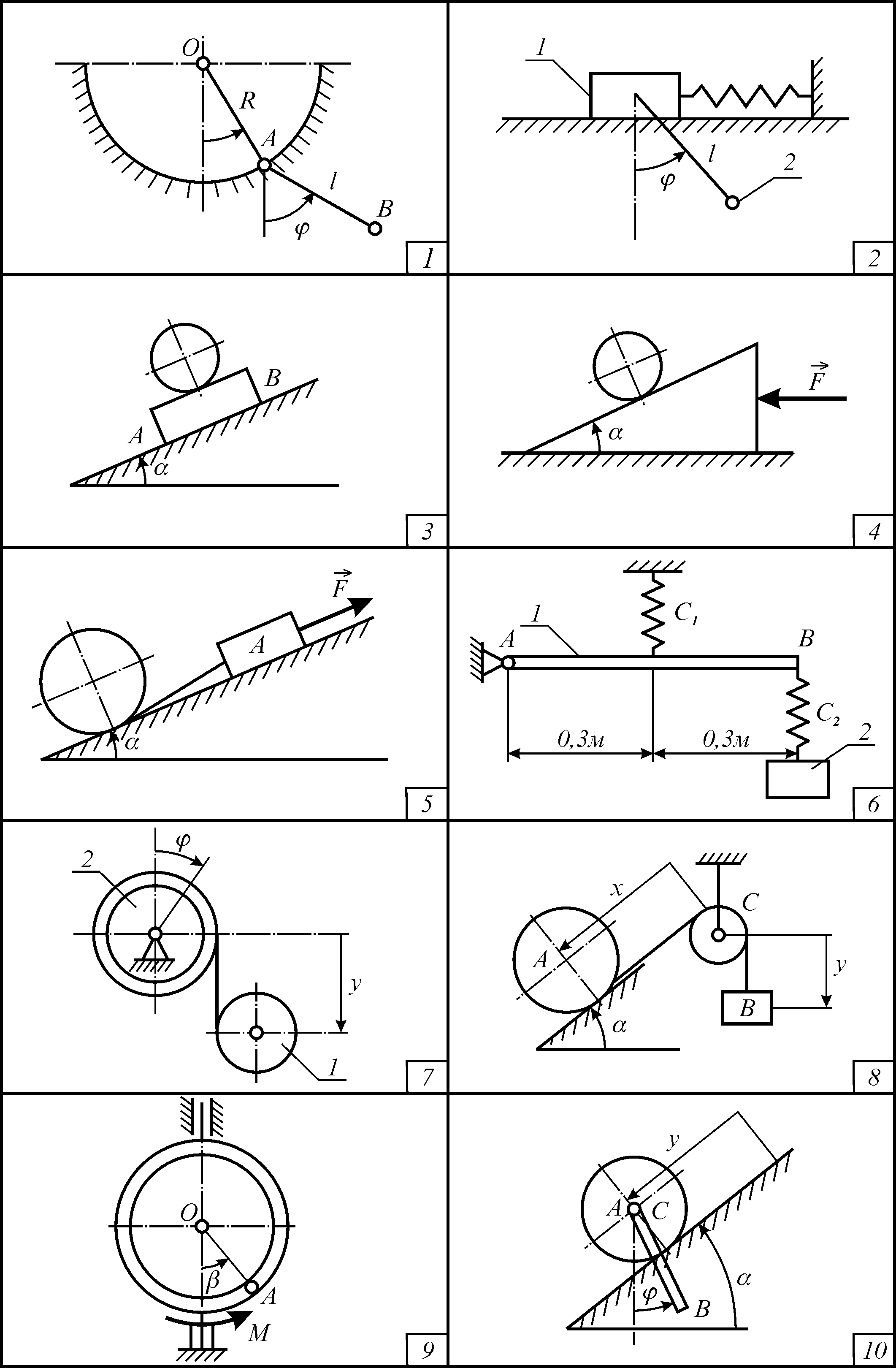
Рисунок Д 16