5.30. Задача д15

Необхідно знати:

5.30.1. Визначення поняття “узагальнені координати системи”:

система параметрів, що однозначно визначають положення матеріального об’єкту.

5.30.2. Число незалежних узагальнених координат голономної системи дорівнює числу степенів її вільності.

5.30.3. Рівняння Лагранжа другого роду

(5.116)

де:

— кінетична енергія системи;

— узагальнена швидкість системи;

— узагальнена координата системи;

— узагальнена сила;

— номер узагальненої координати;

— число степенів вільності системи.

5.30.4. Формули, за якими визначається кінетична енергія механічної системи твердого тіла (див. форм 5.97—5.101).

5.30.5. Способи визначення узагальненої сили:

а) для визначення узагальненої сили, що відповідає деякій —узагальненій координаті, необхідно цій координаті надати приріст ( ), обчислити суму елементарних робіт усіх сил, що діють на систему, на отриманому її переміщенні й отриману роботу поділити на приріст узагальненої координати:

(5.117)

б) узагальнена сила дорівнює похідній, що береться зі знаком мінус, від потенціальної енергії (П) за відповідною узагальненою координатою

(5.118)

5.30.5. Формули, за якими визначається робота сил (див. форм 5.74, 5.77, 5.1045-5.106).

5.30.7. Формулу, що визначає момент інерції кільця (див. форм. 5.102), суцільного однорідного циліндра (див. форм. 5.103).

Необхідно вміти:

5.30.8. Класифікувати рухи твердого тіла.

5.30.9. Проводити кінематичний розрахунок (див. § 5.25.8).

Приклад. 30. Визначити прискорення, з яким обертається шків 1 механічної системи, що зображена на рис. 5.79, якщо:

Рисунок 5.79

Масу кожного шківа вважати рівномірно розподіленою уздовж його зовнішнього ободу. Вантаж 4 — це суцільний однорідний циліндр.

Вантаж ковзає поверхнею без тертя, а також котиться без ковзання. В остаточному розрахунку прийняти м.

Розв’язання.

1. Розглянемо рух даної системи. Вона має одну степінь вільності.

2. Зобразимо сили, що діють на систему (рис. 5.80):

— сили ваги;

— задана сила;

—обертаючі момент;

— нормальні реакції поверхонь;

— реакції підшипників.

Рисунок 5.80

3. Для визначення прискорення шківа 1 складаємо рівняння другого роду для системи, що має одну степінь вільності

(а)

За узагальнену координату вибираємо кут повороту шківа 1 ( ), вважаючи, що шків обертається у напрямку обертаючого моменту . Узагальнена швидкість і рівняння (а) набуває вигляду:

(б)

4. Перш, ніж визначити кінетичну енергію системи, проведемо кінематичний розрахунок — виразимо швидкості всіх ланок механізму через узагальнену швидкість

5. Визначаємо кінетичну енергію системи, що дорівнює сумі кінетичних енергій усіх тіл

(в)

Тіла 1 та 2 здійснюють обертальний рух, значить

При визначенні і моменти інерції шківів обчислювались за формулою оскільки їхня маса рівномірно розподілена уздовж зовнішнього ободу.

Тіло 3 здійснює поступальний рух, значить

Тіло 4 здійснює плоскопаралельний рух, значить

Оскільки тіло 4 — це суцільний однорідний циліндр, то

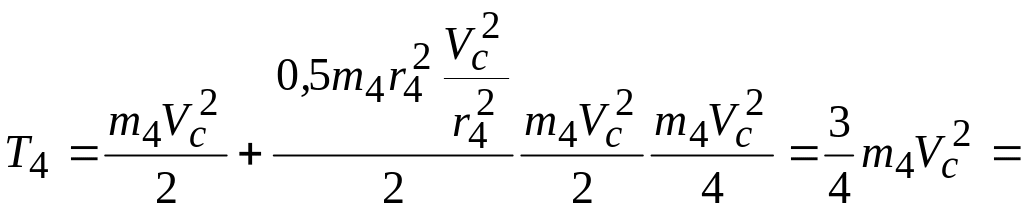
Підставляючи значення у (в), остаточно знайдемо

6. За формулою знайдемо узагальнену силу. Для цього узагальненій координаті надаємо додатній приріст і визначаємо суму елементарних робіт усіх сил, що діють на систему, на отриманому її переміщенні.

З кінематичного розрахунку маємо

тоді

Значить,

Підставляючи значення Т та в рівняння (б), отримаємо

Другий доданок дорівнює нулю, оскільки частинна похідна вимагає явної залежності функції від даного параметру. Тоді

звідки знаходимо

с^-2.

Відповідь: с^-2.