5.25. Задача д10

Необхідно знати:

5.25.1. Теорему про зміну кінетичної енергії системи

(5.95)

Зміна кінетичної енергії системи на деякому її переміщенні дорівнює алгебраїчній сумі робіт всіх зовнішніх і внутрішніх сил, що діють на систему, на цьому переміщенні.

5.25.2. Для незмінної механічної системи (наприклад: абсолютно тверде тіло; система тіл, пов’язаних між собою елементами, що недеформуються тощо) сума робіт внутрішніх сил дорівнює нулю ( =0) і рівняння (5.95) набуває вигляду:

(5.96)

5.25.3. Формулу, за якою визначається кінетична енергія системи

(5.97)

Кінетична енергія системи дорівнює сумі кінетичних енергій всіх об’єктів, що утворюють систему.

5.25.4. Формули, за якими визначається кінематична енергія твердого тіла:

при поступальному русі

(5.98)

при обертальному русі

(5.99)

при плоскопаралельному русі

(5.100)

(5.101)

де: — моменти інерції тіла відносно осей, що проходять відповідно через центр мас та миттєвий центр швидкостей.

5.25.5. Формули, за якими визначаються моменти інерції:

суцільного однорідного циліндра (диска) (рис. 5.65)

(5.102)

тонкого кільця (кругле тіло, маса якого рівномірно розподілена уздовж його ободу) (рис. 5.66)

(5.103)

Рисунок 5.65	Рисунок 5.66

5.25.6. Формули, за якими визначається робота сил:

постійної сили (див. форм. 5.74);

змінної сили

(5.104)

сили тертя

(5.105)

сили ваги (див. форм. 5.75);

моменту сили

(5.106)

Необхідно вміти:

5.25.7. Класифікувати рухи твердого тіла.

5.25.8. Проводити кінематичний розрахунок: за даною швидкістю (переміщенням, прискоренням) визначати швидкість (переміщення, прискорення) всіх об’єктів, що утворюють систему.

Наприклад. Визначити швидкості всіх ланок механізму, зо зображений на рис. 5.67, якщо тіло І рухається з швидкістю й відомі радіуси циліндричних катків ( ) та шківів ( ).

Розв’язання.

Ланки механізму здійснюють такі рухи:

1 — поступальний;

2 та 4 — обертальний навколо нерухомої осі;

3 та 5 — плоскопаралельний.

Значить, для 2 та 4 необхідно визначити їхні кутові швидкості, для тіл 3 та 5 — кутові швидкості й швидкості їхніх центрів мас.

Рисунок 5.67

З рис. 5.67 видно, що

Тут в основному використані такі положення з кінематики:

1). Швидкість точки тіла, що обертається навколо нерухомої осі, дорівнює добуткові кутової швидкості на її відстань до осі обертання — радіус ( ).

2). Швидкість точки тіла, що здійснює плоскопаралельний рух, дорівнює добуткові кутової швидкості на її відстань до миттєвого центру швидкостей ( ).

Зв’язок між переміщенням можна знайти шляхом інтегрування за часом (при нульових початкових умовах) залежностей між швидкостями, бо . Із співвідношення (а) отримуємо

(б)

Оскільки то диференціючи за часом співвідношення (а), визначимо зв’язок між прискореннями

(в)

Приклад 25. Механічна система (рис. 5.68) складається з вантажів 1 і 3 (коефіцієнт тертя їх об поверхні ), циліндричного суцільного однорідного катка 5 та ступінчастих шківів 2 і 4, радіуси ступенів м, м, 0,2 м; 0,1 м (масу кожного шківа вважати рівномірно розподіленою уздовж зовнішнього ободу). Під дією сили 40 (5+4 ) Н, котра залежить від переміщення точки її прикладення, система приходить у рух. При русі системи на шківи 2 та 4 діють моменти опору та . Визначити швидкість вантажу 3 в той момент, коли переміщення точки прикладення сили дорівнює м, якщо 4 кг, 6 кг, 10 кг, 4 кг, 8 кг, 0,4 Нм.

Рисунок 5.68

Розв’язання.

1. Розглянемо рух механічної системи

2. На систему діють (рис. 5.69):

— сили ваги;

— сили тертя;

— момент сили опору;

— нормальні реакції поверхонь;

— реакції підшипників.

3. Для визначення скористаємося теоремою про зміну кінетичної енергії системи

Рисунок 5.69

Так як у початковий момент система перебувала в спокої, то . Дорівнює нулю й сума робіт внутрішніх сил ( ), оскільки система, що розглядається, є незмінною. Отже, маємо

(а)

4. Перш, ніж визначити кінетичну енергію системи, проведемо кінематичний розрахунок. Оскільки потрібно визначити швидкість вантажу З, задамося й виразимо швидкості всіх ланок механізму через шукану швидкість. З рис. 5.69 видно, що

5. Визначаємо кінетичну енергію системи як суму кінетичних енергій ланок, що входять до системи

(б)

Тіло 1 здійснює поступальний рух, значить,

Тіло 2 здійснює обертальний рух, значить,

Тіло 3 здійснює поступальний рух, значить,

Тіло 4 здійснює обертальний рух, значить,

Тіло 5 здійснює плоскопаралельий рух, значить,

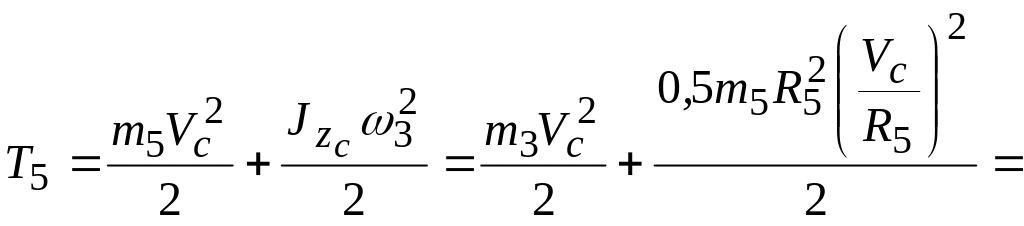
Примітка: моменти інерції шківів 2 та 4 визначалися за формулою оскільки їхня маса рівномірно розподілена уздовж зовнішнього ободу; момент інерції тіла 5, як суцільного однорідного циліндра, визначений за формулою

Підставляючи значення кінетичних енергій ланок у формулу (б), отримаємо значення кінетичної енергії системи

(в)

6. Тепер знайдемо суму робіт усіх зовнішніх сил, що діють на систему, при заданому переміщенні м. Спочатку визначимо переміщення всіх ланок механізму

рад, м;

рад, м.

В результаті отримуємо:

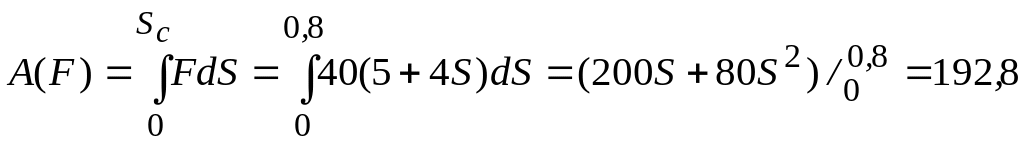Дж;

Дж;

— сила перпендикулярна переміщенню;

— сили прикладені до нерухомої точки;

Дж;

— сили перпендикулярні переміщенню;

Дж;

— сили прикладені до нерухомої точки;

— сила перпендикулярна переміщенню;

Дж;

Дж.

Остаточно маємо

Дж.

Підставляючи значення Т (форм. (в)) та у рівняння (а), отримуємо

(г)

звідки

м/с.

Примітка: При визначенні прискорення тіла 3 необхідно рівняння (г) отримати у вигляді

(д)

Тоді, диференціючи за часом рівняння (д)

і знаючи, що і , отримаємо .

Відповідь: З точністю проведених обчислень 1,5 м/с.