5.22. Задача д7

Необхідно знати:

5.22.1. Визначення основних геометричних та динамічних характеристик системи.

5.22.2. Формули, що визначають:

— координати центра мас системи

(5.78)

де: — координати точки, маса якої ; — маса системи;

— осьові моменти інерції системи

(5.79)

де: — відстані точки масою до відповідних координатних осей.

моменти інерції відносно координатних площин

(5.80)

полярний момент інерції системи

(5.81)

де: — відстань точки масою до полюса 0;

кількість руху механічної системи

(5.82)

(5.83)

де: — швидкість точки масою

— швидкість центру мас механічної системи;

кінетичний момент системи відносно осі

(5.84)

де: — проекція вектора швидкості і-тої точки на площину, що перпендикулярна до осі;

— відстань цієї проекції до осі;

кінетичний момент системи відносно центра

(5.85)

кінетичну енергію системи

(5.86)

Необхідно вміти:

5.22.3. Векторну рівність проектувати на вісь (див. § 5.13.9).

5.22.4. Визначити проекції векторного добутку на координатні осі (див. курс вищої математики).

Приклад 22. Розв’язати задачу Д7 контрольної роботи за варіантом 777.

Розв’язання.

У відповідності до даних задачі 7 (див. табл. Д7 а та Д7 б), маємо:

кг, кг, кг,

м/с, м/с, м/с,

м, м, м.

1. Позначимо і визначимо косинус та синус такого кута

2. За формулами (5.78) визначимо координати центра мас системи

м,

м.

м.

3. За формулами (5.79) визначимо осьові моменти інерції:

кгм²;

кгм²;

кгм^2.

Рисунок 5.59

4. За формулами (5.80) визначаємо моменти інерції системи відносно координатних площин

кгм²;

кгм².

5. За формулою (5.81) визначимо полярний момент інерції системи

кгм².

Перевірка. Знайдені величини задовольняють залежності між моментами інерції

(5.87

6. Так як кількість руху механічної системи визначається формулою (5.82)

то його знаходимо методом проекцій

Нс;

Нс;

Нс;

Нс.

7. За формулою (5.84) знаходимо кінетичний момент системи відносно координатних осей.

оскільки вектори швидкостей точки є паралельними осі ( ) або ж її перетинають ( ).

Нмс;

Нмс.

8. Знаючи проекції кінетичного моменту системи на координатні осі, можна знайти кінетичний момент (головний момент кількості руху) системи відносно початку системи координат:

Нмс.

9. За формулою (5.86) обчислюємо кінетичну енергію системи

Дж.

5.23. Задача д8

Необхідно знати:

5.23.1. Теорему про рух центра мас:

(5.88)

Центр мас механічної системи рухається як матеріальна точка, в котрій зосереджена вся маса системи і до якої прикладені всі зовнішні сили , що діють на систему.

Необхідно вміти:

5.23.2. Класифікувати (на внутрішні та зовнішні) сили, що діють на механічну систему

Зовнішні сили ( )— це сили взаємодії між матеріальними об’єктами різних систем.

5.23.3. Проектувати векторну рівність на вісь (див. § 5.13.9).

5.23.4. Визначити координати центра мас механічної системи (див. форм. 5.78).

5.23.5. Визначати швидкість (переміщення) точки у складному русі (див. § 5.13.2).

5.23.6. Інтегрувати диференційні рівняння.

Приклад 23. Розв’язати задачу Д8 контрольної роботи за варіантом 888.

У відповідності до даних задачі Д8 (див. табл. Д8 а та Д8 б),

кг; кг; кг;

м; Н; м; м.

1. Розглядаємо систему, що складається з плити й точки та у поточний момент часу (рис. 5.60).

Зображуємо всі зовнішні сили, що діють на систему:

— вага плити;

— ваги точок;

— прикладена сила;

Рисунок 5.60

— нормальна реакція горизонтальних направляючих.

Вибираємо систему координат, як вказано на рис. 5.60.

4. Для розв’язання задачі застосуємо теорему про рух центра мас (рівн. 5.88)

Для нашого прикладу

(а)

5. Для дослідження руху плити вздовж горизонталі проектуємо рівн. (а) на вісь абсцис:

(б)

де: — маса системи

кг;

— проекція вектора прискорення центра мас системи на вісь абсцис.

6. За формулою

знаходимо — координату центра мас

де: — поточна координата точки — центру плити

Отже

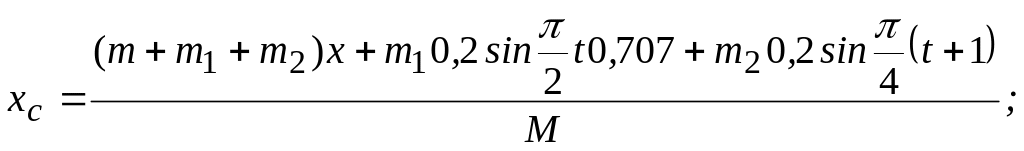
Двічі диференціючи за часом, отримаємо

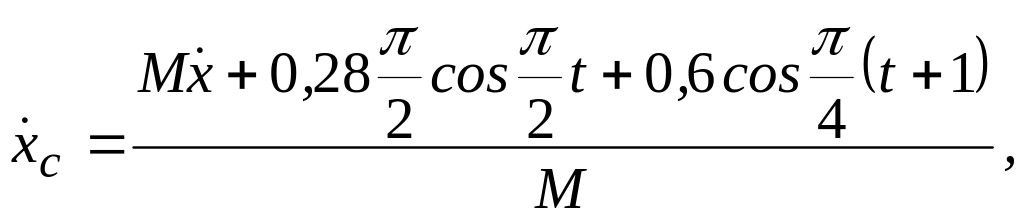
(в)

Підставляючи (в) в рівн. (б), отримаємо

Звідки

(г)

Отримане рівняння є диференційним рівнянням руху плити уздовж горизонталі.

Двічі інтегруючи дане рівняння, отримаємо:

де: та — константи інтегрування, що визначаються з початкових умов. При швидкість плити дорівнює нулю ( ), і припускаємо, що значить:

Отже

(д)

(е)

Отримані рівняння являють собою:

рівн. (д) — закон зміни швидкості плити;

рівн. (е) — закон руху плити уздовж горизонталі.

З рівн. (г, д, е) можна знайти прискорення, швидкість і переміщення плити в будь-який момент часу. Зокрема, при с.

м/с²;

м/с;

м.

7. Для визначення тиску плити на горизонтальні направляючі спроектуємо рівн. (а) на вісь ординат:

Звідки

За формулою

знаходимо — координату центра мас системи (див. рис. 5.60)

Підставляючи відомі величини

Звідки

При с м/с².

Знайдене значення підставляємо в рівн. (ж) і визначаємо нормальну реакцію горизонтальних направляючих

Н.

Тиск плити на горизонтальні направляючі буде таким самим, але спрямованим униз.