
- •Передмова
- •І програма -питання
- •1 Статика твердого тіла
- •2 Кінематика
- •3 Динаміка
- •2 Методичні вказівки щодо вивчення теоретичного матеріалу
- •3 Знання та вміння, що необхідні для розв’язання більшості задач
- •3.1. В’язі, реакції в’язей
- •3.2. Проекція сили на вісь
- •3.3. Момент сили відносно точки
- •Рекомендація
- •3.4. Момент сили відносно осі
- •3.5. Пара сил та її момент
- •4 Загальні методичні вказівки до р08в’язання задач з кожного розділу курсу
- •4.1 Алгоритм розв’язання задач на рівновагу:
- •4.2 Алгоритм розв’язання задач кінематики:
- •4.2.1. Виділити матеріальний об’єкт (точку, тверде тіло), кінематичні характеристики руху якого необхідно визначити.
- •4.2.2. Встановити рух, який здійснює виділений матеріальний об’єкт. При цьому необхідно пам’ятати що:
- •4.2.3. Ще раз повторити теоретичний матеріал відповідно даної теми (руху), виписавши й застосувавши формули, за долом гою яких по заданим величинам визначаються шукані кінематичні характеристики руху.
- •1. Пряма задача (перша задача динаміки). За відомими кінематичними характеристиками руху матеріального об’єкту визначаються сили, що діють на цей об’єкт.
- •4.3. Алгоритм розв’язання задач динаміки:
- •5 Kоhкpethi методичні вказівки до розв’язань задач
- •5.1. Задача с1
- •5.1.3. Теорему про три сили.
- •5.1.4. Геометричну умову рівноваги системи збіжних сил. Для рівноваги системи збіжних сил необхідно й достатньо, щоб векторний (силовий) багатокутник, побудований із сил, був замкнутим.
- •5.2. Задача с2
- •5.3. Задача с3.
- •5.4.2. Рівняння рівноваги плоскої системи сил - рівн. 5.6, 5.7, 5.8.
- •5.5 Задача с5
- •5.6. Задача с6
- •5.7. Задача с7
- •5.7.2. Спосіб розбиття.
- •5.7.3. Спосіб від’ємних площ.
- •5.8. Задача с8
- •5.9. Задача к1
- •5.10. Задача к2
- •5.11. Задача к3
- •5.12. Задача к4
- •5.13. Задача к5
- •5.14. Задача к6
- •5.15. Задача к7
- •5.16. Задача д1
- •5.17. Задача д2
- •5.18. Задача д3
- •5.19 Задача д4
- •5.20. Задача д5
- •5.21. Задача д6
- •5.22. Задача д7
- •5.23. Задача д8
- •5.24. Задача д9
- •5.25. Задача д10
- •5.26. Задача д11
- •5.27. Задача д12
- •5.28. Задача д13
- •5.29. Задача д14
- •5.30. Задача д15
- •5.31. Задача д16
- •6 Вибір варіантів контрольних завдань. Вимоги, що ставляться до виконання робіт та контрольні завдання
- •Задача с1
- •Задача с2
- •Задача с3
- •Задача с4
- •Задача с5
- •Задача с 6-1
- •Задача с 6-2
- •Задача с7
- •Задача с8
- •Задача к1
- •Задача к2
- •Задача к3
- •Задача к4
- •Задача к5
- •Задача к6
- •Задача к7
- •Задача д1
- •Задача д2
- •Задача д3
- •Задача д4
- •Задача д5
- •Задача д6
- •Задача д7
- •Задача д8
- •Задача д9
- •Задача д10
- •Задача д11
- •Задача д12
- •7 Перелік типових задач
- •Література
- •Взірець виконання розрахункової роботи
- •1.1 Визначення напряму руху механізму
- •1.2 Кінематичний розрахунок
- •1.3 Визначення прискорення вантажу методом складання диференціальних рівнянь руху кожної ланки механізму
- •1.4 Визначення прискорення вантажу за теоремою про зміну моменту кількості руху механічної системи
- •1.5 Визначення прискорення вантажу по теоремі про зміну кінетичної енергії системи
- •1.6 Визначення прискорення вантажу за загальним рівнянням динаміки
- •1.7 Визначення прискорення вантажу за рівнянням Лагранжа іі роду
- •1.8 Числовий розрахунок прискорення вантажу
- •1.9 Визначення швидкості вантажу з механізму
- •1.10 Визначення натягу нитки
5.18. Задача д3
Необхідно знати:
5.18.1. Диференційні рівняння руху матеріальної точки в проекціях на декартові осі координат (рівн. 5.65)
Необхідно вміти:
5.18.2. Проектувати сили на декартові осі координат (див. § 3.2).
5.18.3. Розв’язувати другу основну задачу динаміки. Для цього необхідно вміти:
а) інтегрувати диференційні рівняння ( курс вищої математики);
б) визначати константи інтегрування.
Приклад 18.
Тіло масою
![]() кг,
отримавши в точці
початкову швидкість
кг,
отримавши в точці
початкову швидкість
![]() м/с,
рухається в зігнутій трубці
м/с,
рухається в зігнутій трубці
![]() ,
що розташована у вертикальній площині.
На ділянці
на тіло крім сили ваги діє, як вказано
на рис. 5.46, постійна сила
,
що розташована у вертикальній площині.
На ділянці
на тіло крім сили ваги діє, як вказано
на рис. 5.46, постійна сила
![]() Н
і сила опору середовища
Н
і сила опору середовища
![]() Н.
Н.

Рисунок 5.46
Пройшовши відстань
![]() м,
тіло
м,
тіло
![]() у точці
,
не змінюючи значення своєї швидкості.
переходить на ділянку
у точці
,
не змінюючи значення своєї швидкості.
переходить на ділянку
![]() труби, де на нього крім сили ваги діє
змінна сила
труби, де на нього крім сили ваги діє
змінна сила
![]() м/с2,
що спрямована уздовж цієї ділянки.
Нехтуючи тертям, знайти закон руху тіла
на ділянці
.
Прийняти
м/с2,
що спрямована уздовж цієї ділянки.
Нехтуючи тертям, знайти закон руху тіла
на ділянці
.
Прийняти![]() м/с2.
м/с2.
Розв’язання:
1. Вважаючи тіло матеріальною точкою, розглянемо його рух на ділянці .
2. На тіло
діють (рис. 5.47):
![]() — сила ваги;
— задана постійна сила;
— сила опору;
— нормальна реакція поверхні.
— сила ваги;
— задана постійна сила;
— сила опору;
— нормальна реакція поверхні.

Рисунок 5.47
3. Вибрана система координат вказана на рис. 5.47.
4. Складемо
диференційне рівняння руху точки вздовж
осі
![]() :
:
![]() .
.
У відповідності з рис. 5.47 маємо
![]()
Підставляючи чисельні значення
![]()
отримуємо диференційне рівняння руху тіла на ділянці
![]() .
(а)
.
(а)
Оскільки
![]() ,
,
то отримане рівняння (а) приймає вигляд
![]()
або
![]() .
(б)
.
(б)
Отримане диференційне рівняння є рівнянням першого порядку з відокремленими змінними. Відокремлюючи змінні, маємо
![]() ,
,
звідки
![]() .
(в)
.
(в)
Константу
інтегрування
знаходимо з початкових умов (![]() ,
,
![]() ,
,
![]() м/с),
м/с),
![]()
![]()
![]()
Підставивши в рівняння (в), отримаємо
![]() ;
;
![]() ;
;
![]()
звідки,
![]() . (г)
. (г)
Формула (г) — це
закон зміни швидкості тіла
![]() на
ділянці
.
на
ділянці
.
Підставивши
![]() м.
знайдемо швидкість тіла
в
положенні
м.
знайдемо швидкість тіла
в
положенні
![]() м/с.
м/с.
5. Тепер розглянемо
рух вантажу на ділянці
.
Знайдена швидкість
![]() для руху на ділянці буде початковою.
для руху на ділянці буде початковою.
6. Зображуємо тіло в довільному положенні цієї ділянки й прикладаємо діючі на нього сили (рис. 5.48). Тут же вказана вибрана система координат.
7. Складаємо диференційне рівняння руху на ділянці:
![]() .
.

Рисунок 5.48
У відповідності з рис. 5.48, маємо
![]()
Підставивши відомі
значення і представивши
![]() отримаємо
отримаємо
![]()
або
![]() (д)
(д)
Перемноживши
обидві частини (д) на
![]() й інтегруючи, знайдемо
й інтегруючи, знайдемо
![]() (е)
(е)
Константу
інтегрування
знаходимо з початкових умов. При
![]() значить
значить
![]()
звідки
![]()
При знайденому значенні рівняння (е) приймає вигляд
![]()
Множачи обидві частини на і знову інтегруючи, знайдемо
![]()
Оскільки при
![]() то
то
![]() і остаточно отримаємо
і остаточно отримаємо
![]()
Отримане рівняння
є шуканим законом руху тіла на ділянці
ВС.
У цьому рівнянні
![]() — в метрах,
— в секундах.
— в метрах,
— в секундах.
5.19 Задача д4
Необхідно знати:
5.19.1. Основні положення теорії “Прямолінійні коливання матеріальної точки”.
5.19.2. Формулу, за якою обчислюється статичне видовження пружини:
![]() (5.67)
(5.67)
де:
— постійна сила, що діє на пружину;
![]() — коефіцієнт жорсткості пружини.
— коефіцієнт жорсткості пружини.
Необхідно вміти:
5.19.3. Складати диференційні рівняння руху матеріальної точки (рівн.5.67).
5.19.4. Інтегрувати диференційні рівняння, особливо — рівняння другого порядку.
5.19.5. Раціонально вибирати систему координат.
-
Для спрощення розв’язання задач рекомендується початок координат розміщувати в положенні статичної рівноваги вантажу, тобто в положенні, де постійні сили, що діють на пружину, зрівноважуються силою пружності.
5.19.6. Розрахувати коефіцієнт жорсткості (С) пружини, котра є еквівалентною двом пружинам, жорсткості яких та (рис. 5.49).

Рисунок 5.49
Приклад 19. Розв’язати задачу Д4 контрольної роботи за варіантом 444.
Розв’язання.
У відповідності з даними до задачі Д; (див. табл. Д4 а, Д4 б, маємо):
-
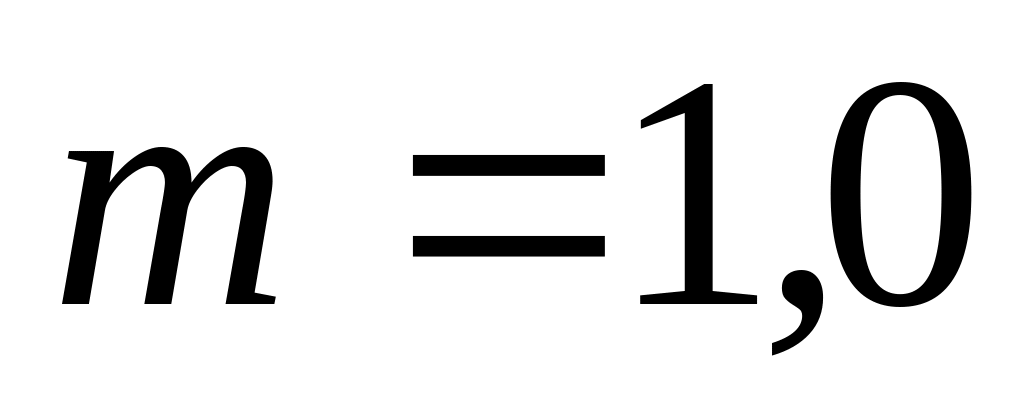 кг;
кг;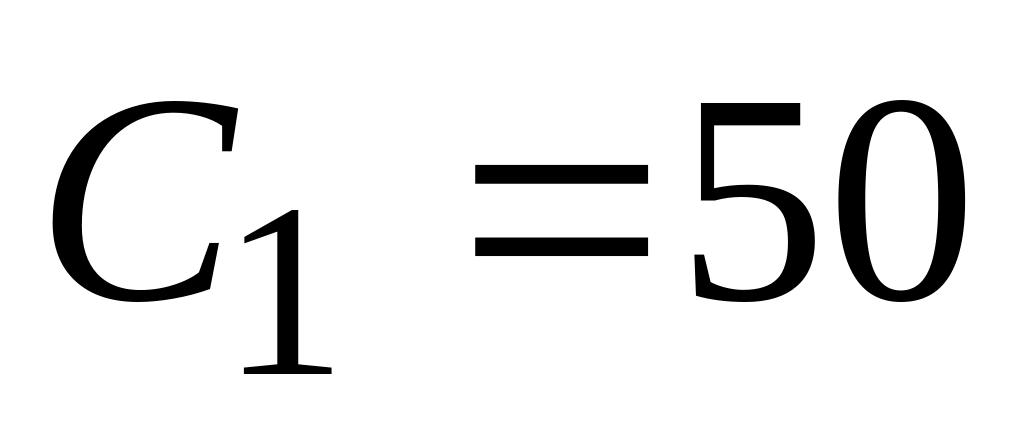 Н/м;
Н/м;Н/м;
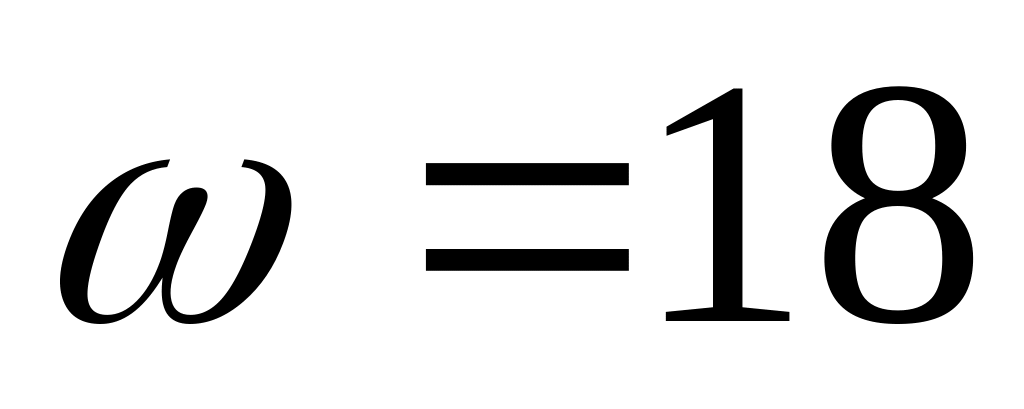 с-1;
с-1;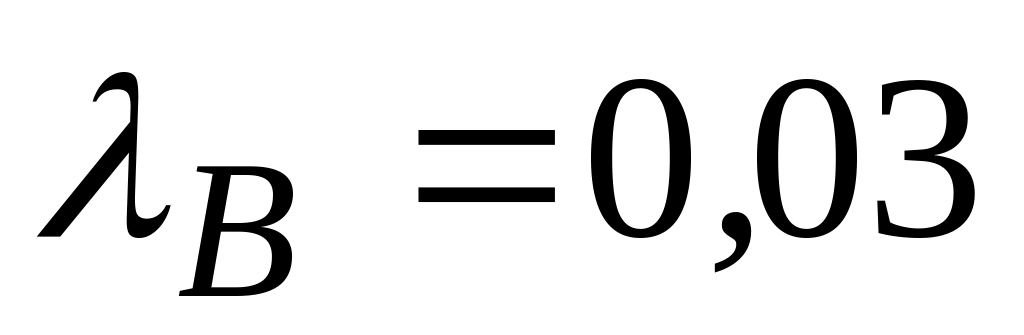 м;
м;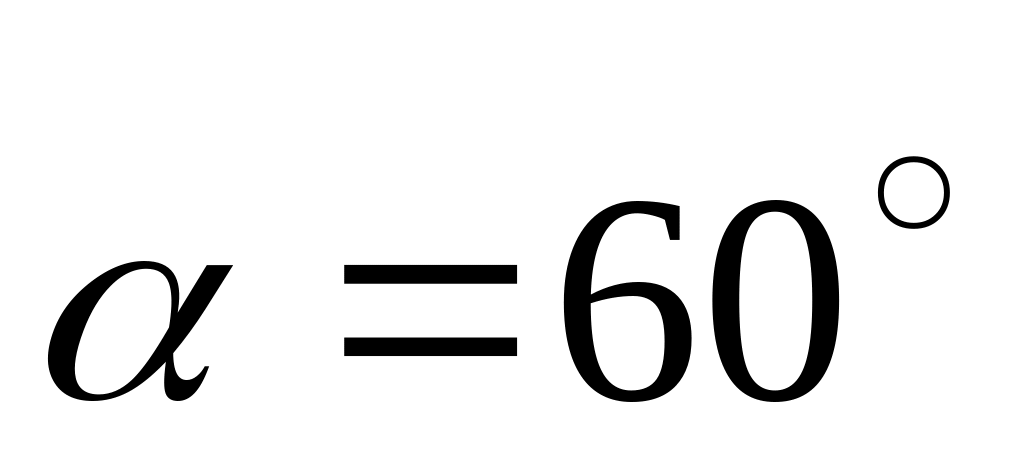 ;
;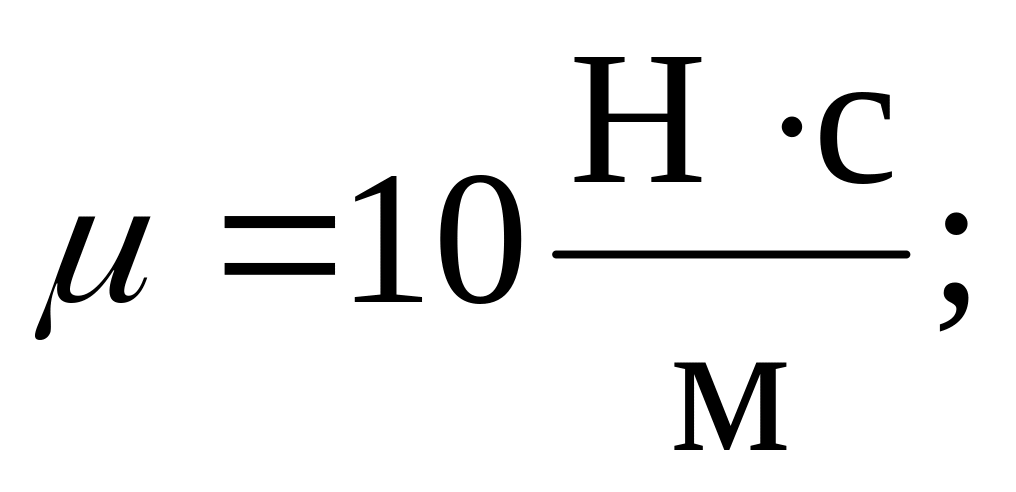
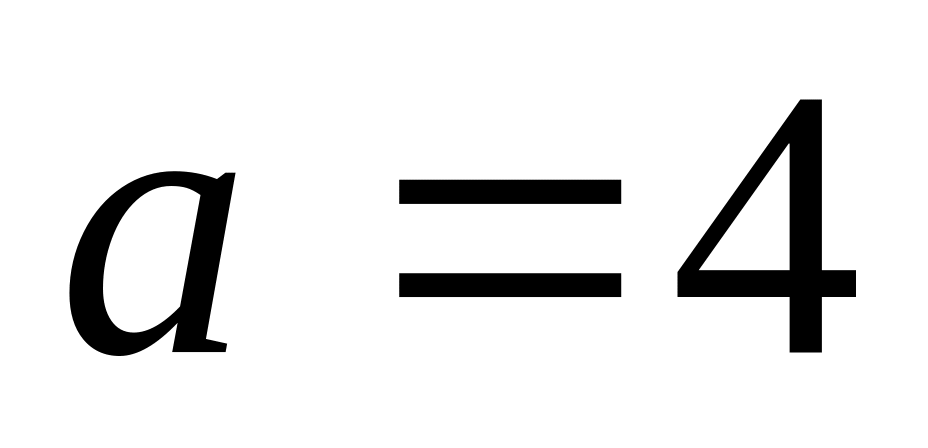 Н;
Н;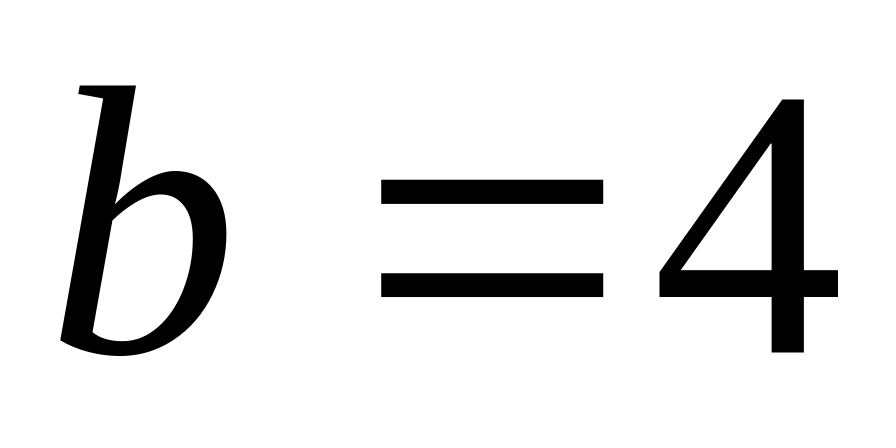 Н;
Н; м/с.
м/с.

Рисунок 5.50
1. Зображуємо вантаж Д, на закріплений до пружини, що еквівалентна заданим пружинам, у поточний момент часу — рис. 5.51, на якому:
![]() — довжина пружини
в не деформованому стані;
— довжина пружини
в не деформованому стані;
![]() — її статичне
видовження;
— її статичне
видовження;
![]() — початок осі
;
— початок осі
;
— поточна координата вантажу.

Рисунок 5.51
Жорсткість еквівалентної пружини
![]() Н/м
Н/м
Статичне видовження пружини
![]() м.
м.
2. Зображуємо сили, що діють на вантаж Д (рис. 5.51):
вага вантажу;
![]() — нормальна реакція
направляючих АВ;
— нормальна реакція
направляючих АВ;
— сила опору, величина якої визначаються за формулою:
![]()
— вага пружності пружини. Величина її визначається за формулою:
![]()
— збурююча сила:
![]()
3. Вибираємо систему координат. Початок осі вміщено у положення статичної рівноваги. Сама вісь проведена уздовж направляючої АВ (рис. 5.52).
4. Складаємо диференційне рівняння руху вантажу:
![]()
![]()
Підставляючи значення сили пружності і розкриваючи дужки, отримуємо
![]()
![]()
![]() (а)
(а)
Отримане рівняння (а) є диференційним рівнянням руху вантажу Д. З математичної точки зору це є неоднорідне лінійне диференційне рівняння другого порядку. Розв’язання його складається з двох частин
![]() (б)
(б)
де:
![]() — загальне рівняння відповідного
однорідного рівняння.
— загальне рівняння відповідного
однорідного рівняння.
![]() (в)
(в)
![]() — часткове рівняння
неоднорідного рівняння.
— часткове рівняння
неоднорідного рівняння.
Для знаходження складаємо характеристичне рівняння
![]()
![]()
Так як корені характеристичного рівняння є комплексними, то розв’язання рівняння (в) має вигляд
![]() (г)
(г)
де:
![]() — константи інтегрування, які визначаються
з початкових умов.
— константи інтегрування, які визначаються
з початкових умов.
Часткове рішення неоднорідного рівняння ( ), виходячи з вигляду правої частини рівняння (а), будемо шукати в формі
![]() (д)
(д)
Підставляючи (д) в (а):
![]()
![]()
![]()
і прирівнюючи коефіцієнти при однойменних функціях в обох частинах рівняння:
![]()
![]()
отримуємо систему двох рівнянь
![]()
![]()
з якої знаходимо
![]()
Підставивши рівняння (д) і (г) в рівняння (б), отримаємо загальне рішення диференційного рівняння (а)
![]()
![]() (е)
(е)
Для знаходження
констант інтегрування з початкових
умов (при
![]() )
)
![]() )
рівняння (а) диференціюємо за часом
)
рівняння (а) диференціюємо за часом
![]()
![]()
і підставляючи початкові умови в рівняння (е) та (ж), отримуємо:
![]()
![]()
Підставляючи знайдені величини в рівняння (е), отримаємо закон руху вантажу Д.
Відповідь:
![]()
![]()
