5.6. Задача с6

Необхідно знати:

5.6.1. Рівняння рівноваги довільної просторової системи сил:

(5.16)

Для рівноваги довільної просторової системи сил необхідно й достатньо, щоб суми проекцій всіх сил на кожну з трьох координатних осей та суми їхніх моментів відносно цих осей відповідно дорівнювали нулю.

Необхідно вміти:

5.6.2. Дію.в’язей представляти дією їхніх реакцій (див. § 3.1 табл. 1).

5.6.3. Проектувати вектор сили на координатній осі (див. § 6.2.).

5.6.4. Визначити момент сили відносно координатних осей (див. § 3.4).

Приклад 6-1. Розв’язати задачу С 6-1 контрольної роботи за варіантом ІІІ, згідно до якого: кН, кН,

кН, кНм, АВ = 1,5 м, АД = 2,0 м, м, кН, кНм.

Розв’язання.

1. Розглядаємо рівновагу прямокутного паралелепіпеда (рис. 5.13).

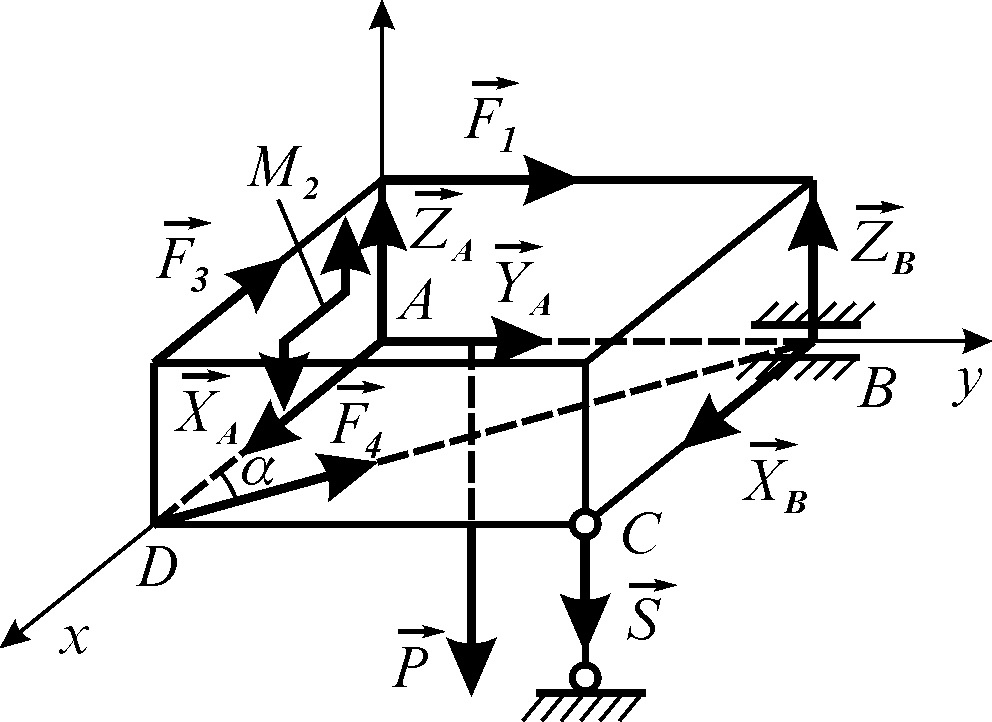
Рисунок 5.13

2. Зображуємо активні сили, що діють на паралелепіпед: пара сил з моментом та його вага , причому

кН.

3. Звільняємо паралелепіпед від в’язей, замінюючи їх дію реакціями: — складові реакції сферичного шарніру; — складові реакції циліндричного шарніра; — реакція невагомого стрижня з шарнірами на кінцях.

4. Вибрана система координат вказана на рис. 5.13.

5. На паралелепіпед діє довільна просторова системи сил. Складаємо рівняння її рівноваги (рівн. 5.16):

Значення та знаходимо з геометричних розмірів

Підставляючи чисельні значення:

Знаходимо значення невідомих величин:

Знак мінус при та вказує, що напрямки даних реакцій протилежні тим, що вказані на рис. 5.13.

Приклад 6-2. Розв’язати задачу С 6-2 контрольної роботи за варіантом 222, відповідно до якого:

Розв’язання.

1. Розглядаємо рівновагу вала (рис. 5.14).

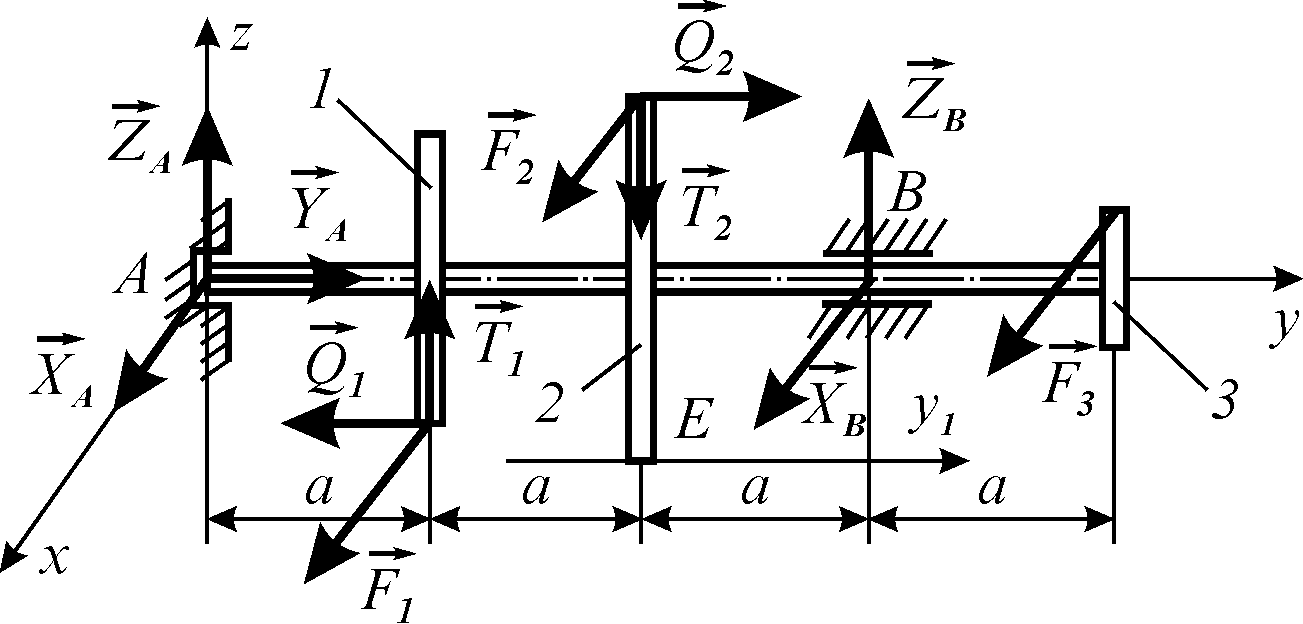
Рисунок 5.14

2. Зображуємо активні сили, що діють на вал:

3. Звільняємо вал від в’язей, замінюючи їх дію реакціями — складові реакції упорного підшипника А; — складові реакції підшипника В.

4. Вибрана система координат вказана на рис. 5.14.

5. На вал діє довільна просторова система сил. Складаємо рівняння її рівноваги:

6. Підставивши чисельні значення:

і розв’язавши отриману систему рівнянь

знаходимо значення невідомих величин

Для перевірки отриманих значень складаємо

Перевірка виконується.

Відповідь.

Знак мінус при значеннях вказує, що напрямки даних реакцій протилежні тим, що вказані на рис. 5.14.

5.7. Задача с7

Необхідно знати:

5.7.1. Формули, що визначають координати центра ваги однорідної плоскої фігури:

(5.17)

у яких: — площа елемента плоскої фігури; — координати його центра ваги.

5.7.2. Спосіб розбиття.

Плоску фігуру розбивають на елементи, центри ваги на площі яких легко визначаються, і за формулами (5.17) знаходять координати центра ваги всієї фігури.

5.7.3. Спосіб від’ємних площ.

В способі розбиття площі вирізаних елементів беруться зі знаком мінус.

5.7.4. Формули, що визначають координати центра ваги геометричних фігур

2. Круговий сектор ONP ( см, )

см² (беремо знак мінус, оскільки сектор є вирізаним).

За формулою (5.19) 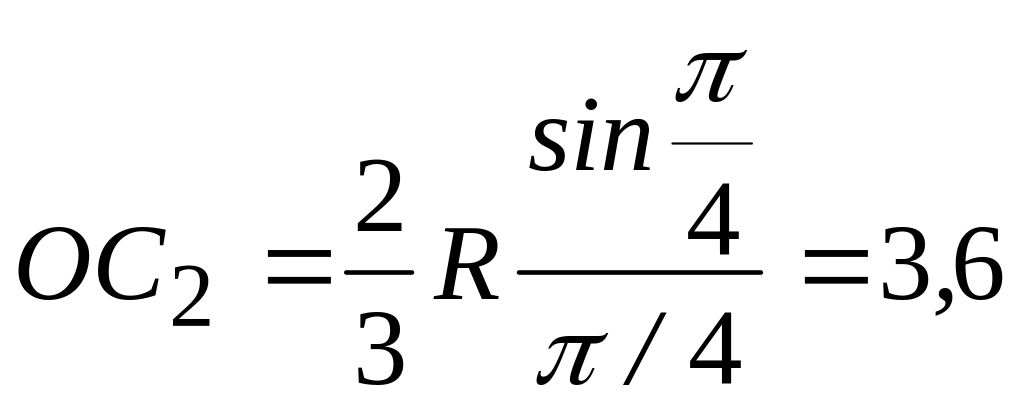см; отримуємо

см;

см.

— трикутника

(5.18)

де: — координати вершин трикутника.

	— кругового сектора (рис. 5.15) (5.19)
Рисунок 5.15

Приклад 7. Знайти координати центра ваги плоскої фігури, що зображена на рис. 5.16. Розміри наведені в см.

Рисунок 5.16

Розв’язання.

Для розв’язання задачі використовуємо метод розбиття в поєднанні з методом від’ємних площ. Виділимо в даній фігурі п’ять частин, знайдемо їхню площу і координати центрів ваги:

1. Прямокутник OАBN.

см²;

см; см.

3. Прямокутник

см²;

см;

см.

4. Прямокутник

см²;

см;

см.

5. Трикутник

см².

Мінус беремо, оскільки трикутник є вирізаний

см;

см.

6. Координати центра ваги заданої плоскої фігури знаходимо за формулами (5.17)

см;

см.

Відповідь:

см; см.