5.4.2. Рівняння рівноваги плоскої системи сил - рівн. 5.6, 5.7, 5.8.

Необхідно вміти:

Див. попередню задачу — пункти 5.3.2-5.3.6.

Приклад 4. Однорідні бруси АС вагою та ВС вагою розташовані у вертикальній площині й з’єднані поміж собою шарніром С (рис. 5.9). Визначити реакції в’язей та зусилля в проміжному шарнірі, якщо:

20 Нм, м.

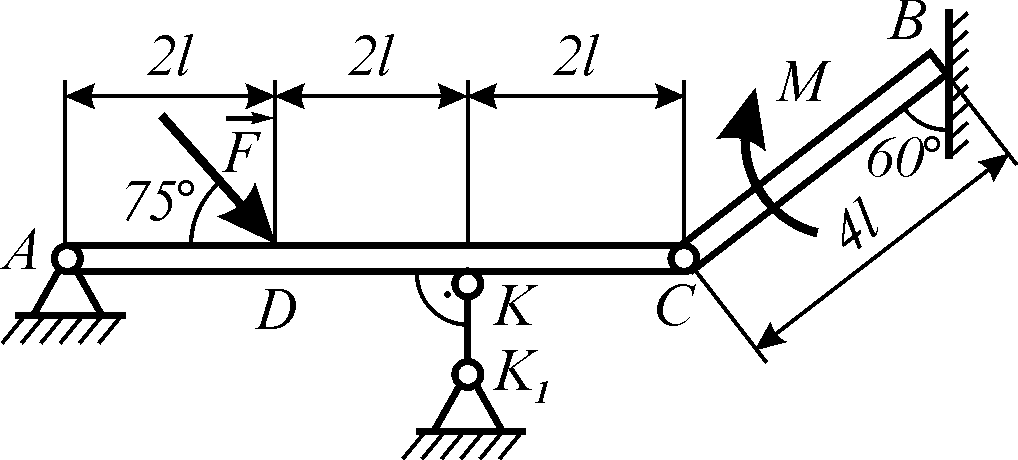
Рисунок 5.9

Розв’язання.

Оскільки за умовою задачі необхідно визначити зусилля (реакцію) в з’єднувальному шарнірі, то задачу розв’язуємо способом розчленіння, тобто розглядаємо рівновагу кожного тіла окремо.

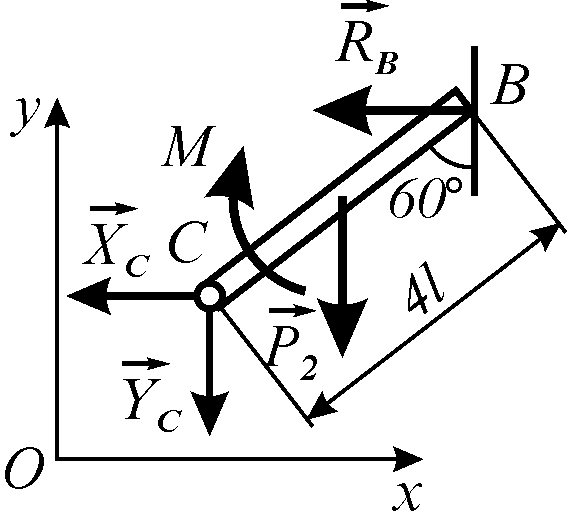
Розглянемо рівновагу бруса ВС, на який (див. рис. 5.10) діють: — вага бруса, задана сила; — пара сил; — реакція вертикальної стінки; — реакція шарніра С. Вибрана система координат вказана на рис. 5.10. На брус діє плоска система сил.

	Для даної системи сил складаємо рівняння рівноваги
Рисунок 5.10

Підставивши чисельні значення, знайдемо невідомі величини

Н;

Розглянемо рівновагу бруса АС, на котрий (див. рис. 5.11) діють: — задані сили; — реакції нерухомого циліндричного шарніра; — реакція невагомого стрижня з шарнірами на кінцях; — реакція шарніра С.

Примітка: Згідно із законом дії та протидії , , а значить та на рисунку повинні бути відкладені у напрямках, протилежних та (див. рис. 5.10). Вибрана система координат вказана на рис. 5.11. На брус діє плоска система сил, рівняннями рівноваги якої є

Рисунок 5.11

Підставивши чисельні значення знайдемо невідомі величини

Н.

Н;

Н.

Відповідь:

Знак мінус при значенні вказує на те, що напрямок цієї реакції є протилежним вказаному на рисунку. Знаки () при значеннях та вказують на те, що напрямок цих реакцій залежно від вибору тіла, рівновага якого розглядається, може бути двояким.

5.5 Задача с5

Необхідно знати:

5.5.1. Формули, за якими визначаються:

— проекції головного вектора на координатні осі:

(5.10)

• модуль головного вектора

(5.11)

— косинуси спрямовуючих кутів

(5.12)

5.5.2. Формули, за якими визначаються:

— проекції головного моменту на координатні осі:

(5.13)

— модуль головного моменту

(5.14)

— косинуси спрямовуючих кутів

(5.15)

5.5.3. Якщо головний момент системи сил дорівнює нулю, то дана система сил зводиться до рівнодійної, що прикладена в центрі зведення.

5.5.4. Якщо головний вектор системи сил дорівнює нулю, то система сил зводиться до пари сил.

5.5.5. Якщо головний вектор і головний момент системи сил відповідно дорівнюють нулю, то система сил є зрівноваженою.

Необхідно вміти:

5.5.6. Проектувати вектор сили на координатній осі (див. § 3.4).

Приклад 5. Розв’язати задачу С5 контрольної роботи відповідно до варіанту 000.

Розв’язання.

1. Зображуємо задану систему сил (рис. 5.12), де

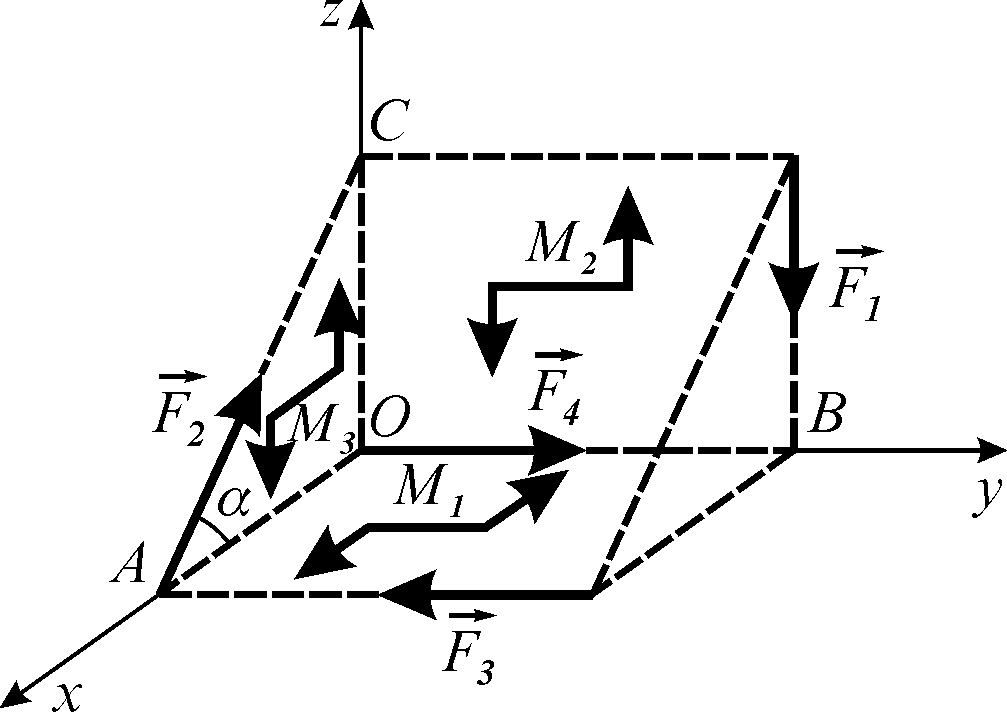
Рисунок 5.12

2. Позначимо причому

3. За формулами (5.10) та (5.11) знаходимо проекції головного вектора та головного моменту сил на координатній осі

(А)

(Б)

4. Підставивши чисельні значення, знаходимо їхні величини

5. Визначаємо величину і напрям головного вектора системи (див. формули 5.12 та 5.13)

;

; ;

.

6. Визначаємо величину й напрямок головного моменту системи (див. формули 5.14 та 5.15)

;

; ;

.

7. Система сил зводиться до рівнодійної, що прикладена в точці приведення, якщо її головний момент відносно цієї точки дорівнює нулю. А це значить, що , , . З рівняння (Б) отримаємо:

Таким чином, при значеннях кНм, 20 кНм, кНм у точці О система зводиться до рівнодійної, величина якої Н.

8. Система сил зводиться до пари сил у тому випадку, коли її головний вектор дорівнює нулю. А це значить, що , , . З рівняння (А) отримаємо:

Таким чином, при значеннях система сил зводиться до пари сил.

9. Система сил буде зрівноваженою в тому випадку, коли її головний вектор ї головний момент відповідно дорівнюють нулю. Це означає, що

З рівнянь (А) та (Б) отримуємо:

Таким чином, при

система сил буде зрівноваженою.