5.2. Задача с2

Необхідно знати:

5.2.1. Рівняння рівноваги системи збіжних сил:

(5.5)

Для рівноваги системи збіжних сил необхідно й достатньо, щоб сума проекцій всіх сил системи на три координаційні осі відповідно дорівнювала б нулю.

5.2.2. Реакція в’язі, здійсненої прямолінійним невагомим стрижнем з шарнірами на кінцях, спрямована уздовж стрижня (див. табл. 1.1).

Необхідно вміти:

5.2.3. Проектувати вектор сили на координатні осі (див. § 3.2).

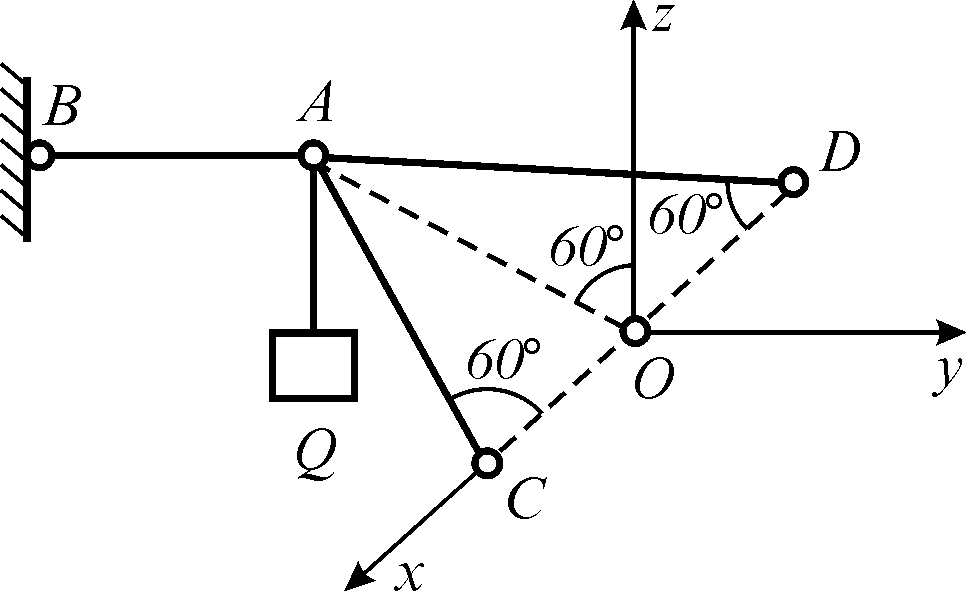
Приклад 2. Знайти зусилля в невагомих стрижнях кон-

	конструкції (див. рис. 5.4), що підтримує вантаж Q = 500 Н, якщо кріплення в точках А, В, С, Д — шарнірні, а стрижень АВ — пара­лельний осі .
Рисунок 5.4

Розв’язання.

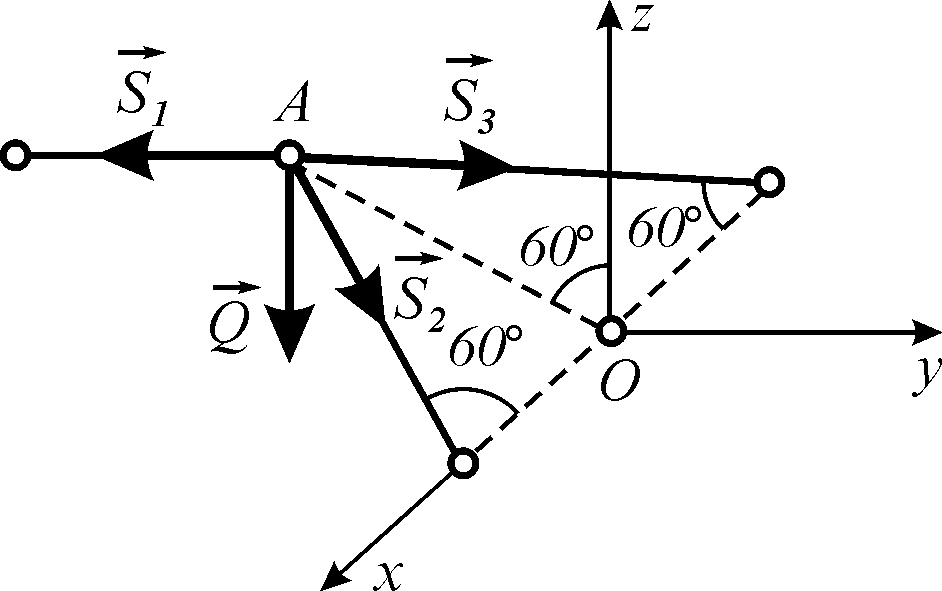
1. Розглядаємо рівновагу шарніра А (рис. 5.5).

	2. На шарнір А діють: - активна сила; - реакції невагомих стрижнів з шарнірами на кінцях. Припус­каємо, що всі стрижні працюють на розтяг. 3. Вибираємо систему коорди­нат, як вказано на рис. 5.5. 4. Так як на шарнір А діє система збіжних сил, складаємо рів­няння рівноваги (рівн. 5.5):
Рисунок 5.5

Примітка: при проектуванні та на координатні осі і застосували положення подвійного проектування (див. § 3.2).

5. Розв’язуємо отриману систему рівнянь

;

.

Підставляючи чисельні значення, отримуємо

Н

Н.

Відповідь:

Знак мінус при значеннях та свідчить, що стрижні працюють на стискання.

5.3. Задача с3.

Необхідно знати:

5.3.1. Рівняння рівноваги плоскої системи сил. Їх можна записати у трьох формах:

а) (5.6)

Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми проекцій усіх сил на кожну з двох координатних осей і сума їх моментів відносно будь-якої точки, що лежить у площині дії сил, відповідно дорівнювали нулю.

6) (5.7)

Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб сума проекцій всіх сил на будь-яку вісь, що лежить у площині дії сил та суми їхніх моментів відносно двох будь-яких точок, що лежать також у площині дії сил, відповідно дорівнювали нулю.

Примітка: точка А та В довільні, але відрізок АВ, що з’єднує точки, не повинен бути перпендикулярним осі, на яку проектуються сили.

в) (5.8)

Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми моментів усіх сил відносно будь-яких трьох точок, що знаходяться у площині дії сил і не лежать на одній прямій, відповідно дорівнювали нулю.

При розв’язанні задачі краще за все застосувати рівняння рівноваги в формулі 5.6, котрі вважаються основними, оскільки:

вони не накладають обмежень на вибір координатних осей і точки, відносно якої складається сума моментів;

складання рівнянь проекцій є задачею більш простою, ніж видання рівнянь моментів.

5.3.2, Дію на тверде тіло рівномірно розподіленого навантаження інтенсивністю можна замінити дією його рівнодійної , обчислюється за формулою

(5.9)

і яка прикладена посередині АВ — ділянки її дії (див. рис. 5.6)

Необхідно вміти:

5.3.3. Дію в’язей замінити дією їхніх реакцій (див. § 3.1) табл. 1.1.

5.3.4. Проектувати вектор сили на координатні осі (див. § 3.2).

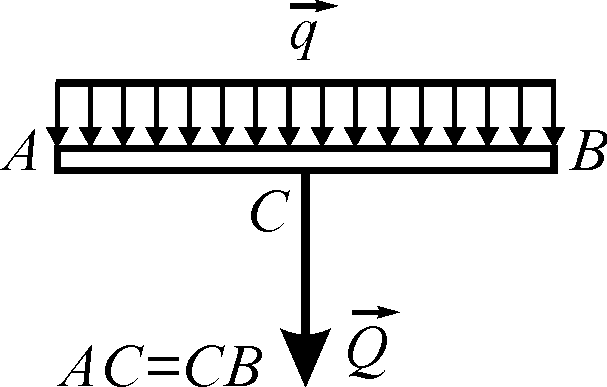
Рисунок 5.6

5.3.5. Визначити момент сили відносно точки (див. § 3.3).

5.3.6. Визначити момент пари сил відносно точки (див. § 3.5).

Приклад. Визначити реакції заробки жорсткої рами АВ, якщо

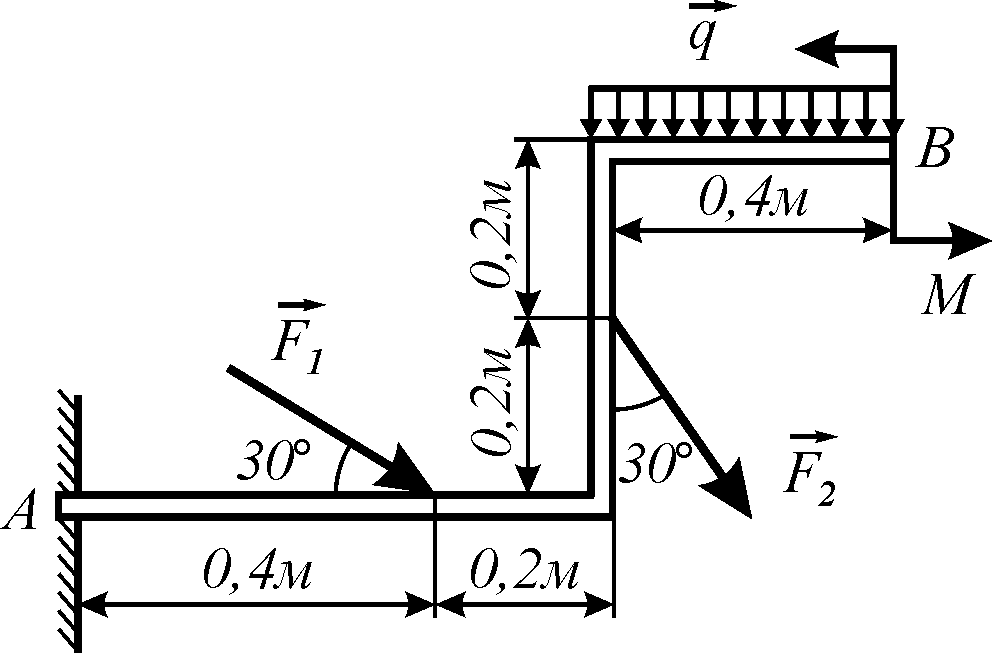
Рисунок 5.7

Розв’язання.

1. Розглядаємо рівновагу рами АВ (рис. 5.8).

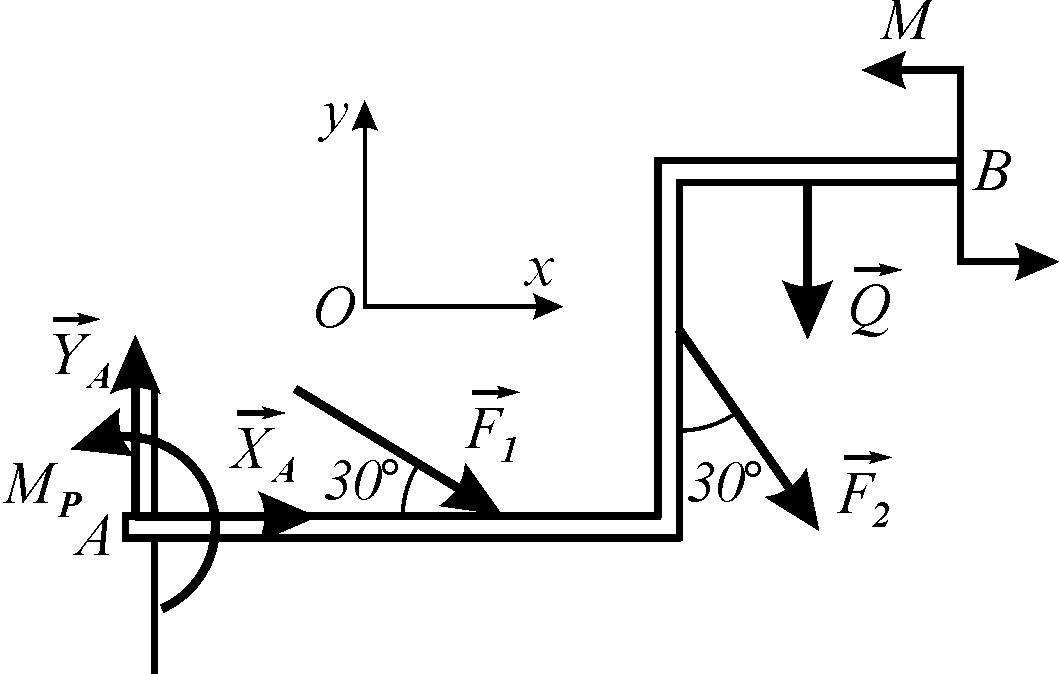
Рисунок 5.8

2. Зображуємо сили, що діють на раму: — задані сили; — рівнодійна рівномірно розподіленого наванта­ження, причому

— момент пари сил.

3. Звільняємо раму від в’язей. В’язею є защемлення. Дія защемлення еквівалентна силі, розкладеній на складові та і з моментом .

4. Вибрана система координат вказана на рис. 5.8.

5. На раму діє довільна плоска система сил. Складаємо рівняння рівноваги (рівн. 5.6):

Підставляючи чисельні значення

знаходимо невідомі величини

Нм.

Для перевірки складемо суму моментів діючих на раму сил відносно точки В:

Отримане значення відповідає точності проведених обчислень і підтверджує достовірність отриманих результатів.

Відповідь. Нм.

Знак мінус при значеннях та вказує на те, що їх напрямки протилежні вказаним на рисунку.

5.4. ЗАДАЧА С4

Необхідно знати:

5.4.1. Якщо конструкція з’єднаних тіл знаходиться в рівновазі, то кожна її складова частина також знаходиться в рівновазі. Таким чином, задачі на рівновагу системи з’єднаних тіл можна на роэв’язувати двома способами;

а) розглядається рівновага кожного тіла окремо (при розгляді рівноваги одного тіла системи останні тіла системи будуть для нього в’язями);

б) розглядається рівновага системи всіх тіл разом узятих, а вже потім розглядається рівновага окремого тіла і складається необхідна кількість рівнянь рівноваги (при розгляді рівноваги системи всіх тіл у рівняння рівноваги не ввійдуть сили, з котрими окремі тіла діють одне на одного, тобто внутрішні сили).

Вибір методу розв’язання задач залежить від умови задачі й навичок того, хто її розв’язує. Можна лише порекомендувати, що коли за умовою задачі не потрібно визначати зусилля в з’єднувальних елементах, то задачу раціональніше розв’язувати другим способом.