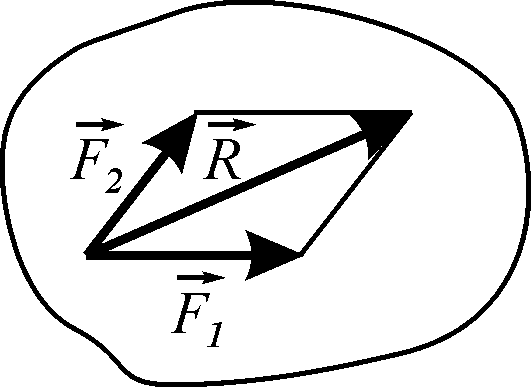1. Пряма задача (перша задача динаміки). За відомими кінематичними характеристиками руху матеріального об’єкту визначаються сили, що діють на цей об’єкт.

2. Обернена задача (друга задача динаміки). По заданим си лам, що діють на матеріальний об’єкт, визначають його кінематич­ні характеристики руху.

Обидві ці задачі розв’язуються за допомогою отриманих у тео­ретичному курсі залежностей між кінематичними характеристиками руху матеріального об’єкту та силами, що діють на нього, за та­ким алгоритмом:

4.3. Алгоритм розв’язання задач динаміки:

4.3.1. Виділити матеріальний об’єкт, рух якого необхідно розглянути для визначення шуканих величин.

4.3.2. Прикласти всі сили як активні, так t пасивні, що діють на виділений об’єкт.

4.3.3. Вибрати систему координат. Осі координат бажано спря­мувати так, щоб для поточного положення координати точки та про­екції швидкості на ці осі були додатними. Якщо тіло здійснює Обертальний рух, то необхідно вказати вісь обертання.

4.3.4. Вибрати метод розв'язання задачі. Існуючі в динаміці методи розв'язання задач, можна об’єднати в три групи:

метод диференційних рівнянь руху;

метод нагальних теорем;

метод загальних принципів.

Для реалізації цього пункту необхідно записати рівняння, що математично виражає закон, теорему, принцип і т.п., який кладеться в основу розв’язання задачі.

4.3.5. Підставивши в записане рівняння необхідні вирази, відомі величини та виконавши відповідні перетворення, визначити шукані величини.

5 Kоhкpethi методичні вказівки до розв’язань задач

Тут коротко викладені ті знання та вміння, котрі є необхідними для розв’язання кожної задачі, а також наведені приклади їх розв’язання.

5.1. Задача с1

Необхідно знати:

5.1.1. Аксіому паралелограма сил.

	Рівнодійна двох сил, лінії дії яких перетинаються в одній точці, виражається діагоналлю паралелограма, побудованого на цих силах (рис. 5.1). Модуль рівнодійної визначається за форму­лою:
Рисунок 5.1

(5.1)

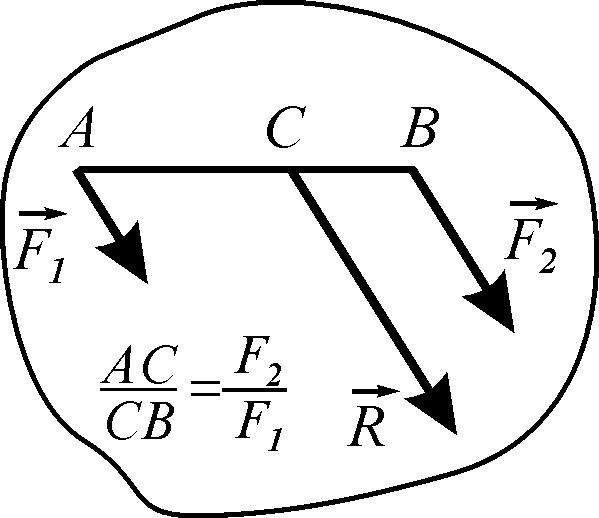
5.1.2. Правило складання двох паралельних сил.

	Рівнодійна двох паралельних сил, що спрямовані в один бік, паралельна цим силам; її модуль дорівнює алгебра­їчній сумі цих сил, а лінія її дії ділить відстань між точками прикладення даних сил на частини, що є обернено пропорційними цим силам (рис. 5.2).
Рисунок 5.2

(5.2)

5.1.3. Теорему про три сили.

Для рівноваги плоскої системи трьох непаралельних сил необ­хідно, щоб лінії їх дії перетинались в одній точці.

5.1.4. Геометричну умову рівноваги системи збіжних сил. Для рівноваги системи збіжних сил необхідно й достатньо, щоб век­торний (силовий) багатокутник, побудований із сил, був замкнутим.

Необхідно вміти:

5.1.5. В’язі представляти їхніми реакціями (див. § 3.1 і табл.1.1).

5.1.6. Будувати силовий багатокутник.

Приклад 1. На стрижень АС вагою Р = 2 кН, що закріплений шарнірно в точці А і спирається в точці В на нерухому опору, як показано на рис. 5.3, а, діє горизонтальна сила F = 4 кН. Геометрично визначити реакції в’язей, що накладені на стрижень, якщо АВ = 0,3 м, ВС = 0,5 м. Отримані результати перевірити аналітично.

Розв’язання (див. алгоритм 4.1). Розглянемо рівновагу стрижня АС. На нього діють (див. рис. 5.3, 6): та — задані сили, що відомі за величиною, напрямком і точками прикладення. На стрижень накладено дві в’язі: опора В, реакція якої спрямована перпендикулярно до стрижня АС, і шарнір А, напрямок реакції якого наперед невідомий. Але в даній задачі, використовуючи теорему про їй сили, можна вказати лінію дії реакції шарніру А і задачу розв’язати геометрично. Для цього:

1. Знаходимо точку Е перетину ліній дії заданих сил та (рис. 5.3, 6).

2. Застосовуючи аксіому паралелограма сил, знаходимо рівнодійну заданих сил та (рис. 5.3, в).

3. Визначимо точку К перетину ліній дії сил та (рис. 5.3, в).

4. З'єднуємо точку К з точкою А. Це й буде лінія дії реакції .

5. Будуємо замкнутий силовий багатокутник (рис. 5.3, г). З точки а, що береться поза основним рисунком, відкладаємо силу . Через початок і кінець сили проводимо прямі, паралельні лініям дії реакцій та ( ). В точках перетину прямих та знаходиться третя вершина силового трикутника. Спрямовуємо вектори реакцій так, щоб у кожній з вершин силового трикутника (рис. 5.3, г) був розташований кінець тільки однієї з сил.

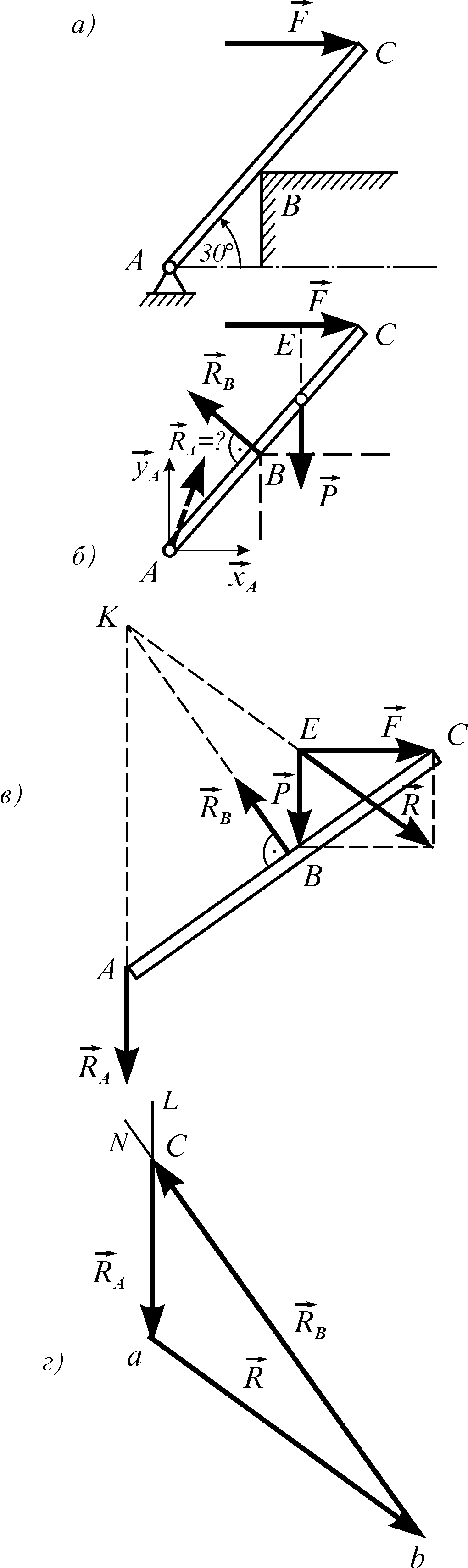
Рисунок 5.3

6. Визначаємо чисельні значення шуканих реакцій:

кН;

(5.3)

кН.

де: — масштаб побудови силового трикутника.

Для аналітичної перевірки рішення складемо рівняння рівноваги сил, що діють на стрижень. Так як на стрижень (див. рис. 5.3, б) діє плоска система сил, скористаємося рівняннями її рівноваги [див. задачу С3).

(5.4)

звідки

кН;

кН;

кН;

кН.

Відповідь: = 4,62 кН. Знак мінус при значеннях свідчить про те, що істинний напрямок вказаних реакцій є протилежним зображеному на рисунку.

Аналітичний розрахунок підтверджує правильність от-риманих геометричним способом результатів.