8. « Численное дифференцирование»
Дифференцирование и интегрирование требуются при решении многих практических задач. Аналитические методы решения по разным причинам могут быть неэффективны или в принципе неприменимы. Вычислительные методы и технологии этих операций намного более универсальны и хорошо разработаны. Хотя они различны для дифференцирования и интегрирования, есть и важные общие черты. Так, в их основе лежат принципы дискретизации и аппроксимации; некоторые варианты используют также принцип итерации.
Можно с определённой долей условности разделить методы на ручные и компьютерные. Для первых- во главу угла ставится фактор уменьшения объёма арифметической части алгоритмов за счёт усложнения их логической структуры, для вторых- предпочтение отдаётся именно простоте логики там, где этого можно достигнуть увеличением арифметической «нагрузки».
Далее будут рассмотрены наиболее употреб. компьютерные методы.
Постановка вопроса
При решении практических задач часто нужно найти производные указанных порядков от функции y=f(x) , заданной таблично. Возможно также , что в силу сложности аналитического выражения непосредственное дифференцирование затруднено.
Для вывода формул приближенного дифференцирования заменяют данную функцию f(x) на интересующем отрезке [a,b] интерполирующей функцией P(x) ( чаще всего полиномом) , а затем полагают : y¢=f ¢(x) , x [a,b]
Аналогично поступают при нахождении производных высших порядков.
Если для интерполирующей функции P(x) известна погрешность
R(x)= f(x) P(x)
То погрешность производной P(x) выражается формулой
r(x) = f (x) P (x) = R (x)
Погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же справедливо для производных высших порядков .
Действительно, близость друг к другу ординат двух кривых f(x) и P(x) на отрезке [a,b] еще не гарантирует близости на этом отрезке их производных f ¢(x) и P(x) , т.е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента.
Численное
дифференцирование – неустойчивый
процесс по отношению к самым малым
вариациям f(x).
Представим
функцию в виде суммы f(x)=f1(x)
+ f2(x),
где
f1(x)
– основная
составляющая выраженно гладкого
характера,
f2(x)
– деформирующее
дополнение
с выраженной негладкостью. Пусть
соотношение евклидовых норм
>
,
т.е. функция f1(x)
«большая»,
а f2(x)
очень «маленькая»; например, f2(x)
представляет собой погрешность измерений
или вычислений значений основной
составляющей.
Тогда f '(x)= f1 '(x) + f2 '(x), при этом баланс евклидовых норм может оказаться противоположным: f1(x)< f2(x); фактически была бы вычислена производная добавки f2(x), а не основной части.
Графическое дифференцирование
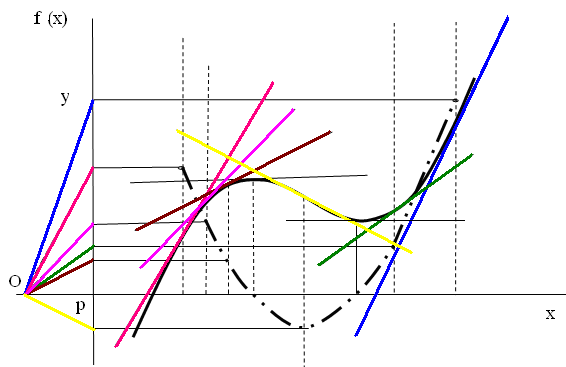
Для практических компьютерных расчётов более или менее часто используются методы симметричных или асимметричных разделённых разностей и дифференцирования интерполяционного полинома в форме Ньютона или Лагранжа. Во всех случаях явно или неявно используется аппарат конечных разностей .
Особняком стоит метод дифференцирования сглаживающего полинома