13 Лекция 6 14.03.2007

Переход от ду высшего порядка к сду первого порядка.

ОДУ n – го порядка называется уравнение с неизвестной функцией , в которое входят производные этой функции вплоть до y⁽ⁿ⁾(x).

В общем виде ОДУ n – го порядка содержит независимую переменную, неизвестную функцию и ее производные (или дифференциалы) до n – го порядка включительно и имеет вид F(x,y,y’,y”,…,y⁽ⁿ⁾)= 0 , где x – независимая переменная, y,y’,y”,…,y⁽ⁿ⁾ – неизвестная функция и ее производные.

ОДУ n – го порядка, разрешенное относительно старшей производной, может быть записано в виде

Для корректной постановки задачи Коши требуется задать n начальных условий на саму функцию y(x) и ее производные от первого до (n-1) порядка включительно , т.е в виде

Положим .

Очевидно , что .

Тогда ДУ порядка n с начальными условиями может быть записано в виде

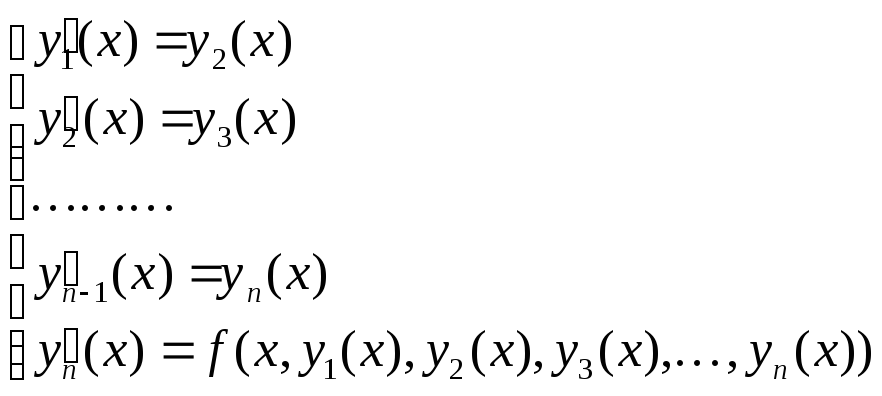
С начальными условиями в новых обозначениях

(12.4)

Мы получили систему ОДУ первого порядка для n функций с n начальными условиями.

Пример 1 :

Рассмотрим численное решение дифференциального уравнения свободных колебаний маятника в сопротивляющейся среде. Еще это уравнение называют уравнением гармонического осциллятора .

Здесь y(t)  изменение угла его отклонения от вертикали ,

y(t) – угловая скорость маятника ,

y(t)  ускорение ,

y(0)=0.1  начальное отклонение ,

y(0)=0  начальная скорость .

График решения

Как можно заметить, результатом применения блока Given/Odesolve является функция y(t), определенная на промежутке (to, ti)

Допустимо, и даже часто предпочтительнее, задание функции Odesolve (t, tl, step) с тремя параметрами, где step- внутренний параметр численного метода, определяющий количество шагов, в которых метод Рунге-Кутты, будет рассчитывать решение дифференциального уравнения.

2. Второй способ решения ОДУ высшего порядка связан со сведением его к эквивалентной системе ОДУ первого порядка.

Любое ОДУ n-го порядка, линейное относительно высшей производной, можно свести к эквивалентной системе n дифференциальных уравнений.

Действительно, если формально обозначить y(t) = y₁(t), a y'(t)=y₂(t)=y₁'(t), то исходное уравнение запишется через функции у₁(t) и y₂(t) в виде системы двух ОДУ

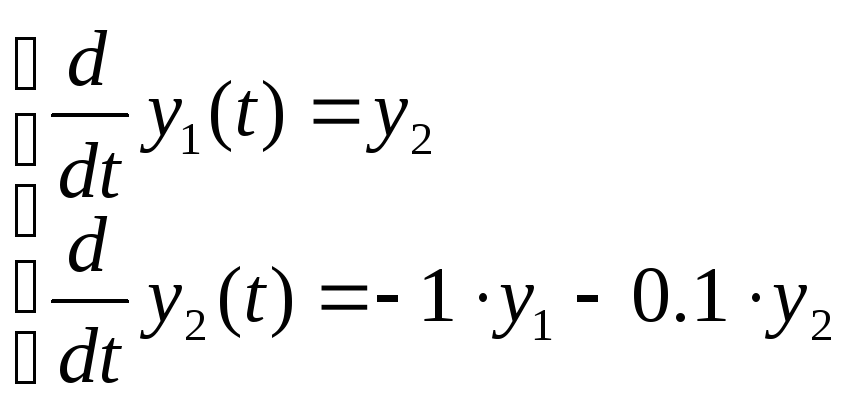При начальных условиях

В случае решения системы методом Рунге-Кутты для первого шага можно записать:

i=0 , t₀=0

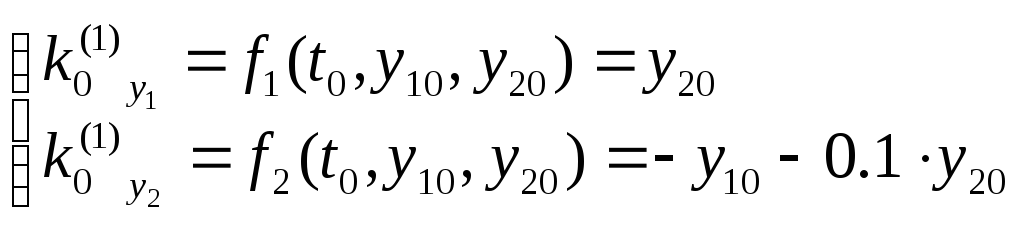
Для :

Значения соответствующих коэффициентов будут

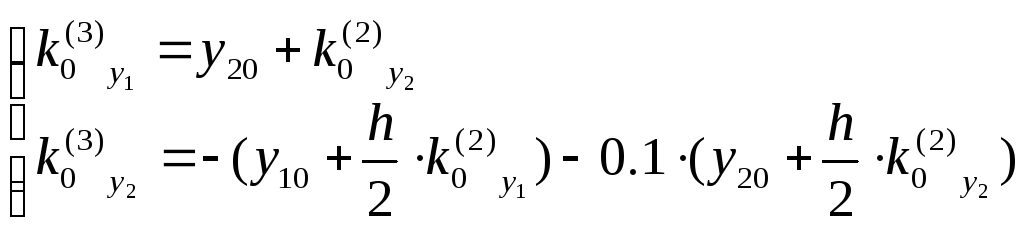
Для :

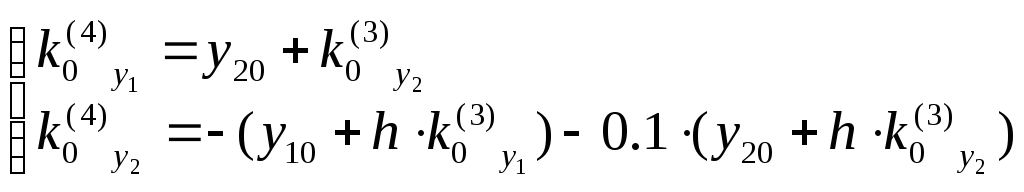
Это решение только для первого шага вычислений по методу Рунге-Кутты.

Использование вычислительной системы mathcad

По умолчанию нумерация строк и столбцов начинается с нуля , поэтому чтобы иметь лишние затруднения , можно просто принять , что y₁=y₀ , а соответственно y₂=y₁ . Это позволит не производить перенумерование элементов матриц условий и решений.

Обратите внимание на необходимость векторной записи как самого уравнения, так и начального условия .

Самая важная - это первая строка, в которой определяется система ОДУ.

1. Функция D должна быть функцией обязательно двух аргументов.

2. Второй ее аргумент должен быть вектором того же размера, что и сама функция D.

3. Точно такой же размер должен быть и у вектора начальных значений уо (он определен во второй строке листинга).

Альтернативный метод решения ОДУ заключается в использовании одной из встроенных функций rkfixed, Rkadapt или Bulstoer.

Встроенные функции, которые позволяют решать поставленную в форме СДУ задачу Коши различными численными методами:

- rkfixed(y0,t0,ti,M,D) - метод Рунге-Кутты с фиксированным шагом;

- Rkadapt(y0,t0,ti,M,D) - метод Рунге-Кутты с переменным шагом (Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений – частыми);

- Bulstoer (y0,t0,ti,M,D) - метод Булирша-Штера ( метод рациональной экстраполяции – сначала находится первоначальное приближение в точках по какому-то из известных одношаговых методов , а затем считают улучшенное с помощью экстраполяции рациональными функциями ) Обычно используется для сложных систем из большого кол-ва ДУ.

• y0 - вектор начальных значений в точке to размера nx1;

• to - начальная точка расчета;

• ti - конечная точка расчета;

• м - число шагов, на которых численный метод находит решение;

• D - векторная функция размера nx1 двух аргументов - скалярного t и векторного у.

При этом у - искомая векторная функция аргумента t того же размера nx1. В подавляющем большинстве случаев достаточно использовать первую функцию rkfixed.

Размер полученной матрицы будет равен (m+1)х(n+1), т. е. 51х3 .