Vychmat_lektsii / Лекция 5 Метод Рунге-Кутты

8

Лекция 5 07.03.2007

Лекция 5 . Метод Рунге – Кутты .

Все рассмотренные ранее численные методы решения ОДУ первого порядка описываются формулами вида y_n+1=y_n+h(x_n,y_n,h), причем для модификаций метода Эйлера функция  имеет вид

(x_n,y_n,h)=a₁f(x_n,y_n)+ a₂f(x_n+b_1h,y_n+b₂hy), y_n=f(x_n,y_n)

Для исправленного метода Эйлера ,

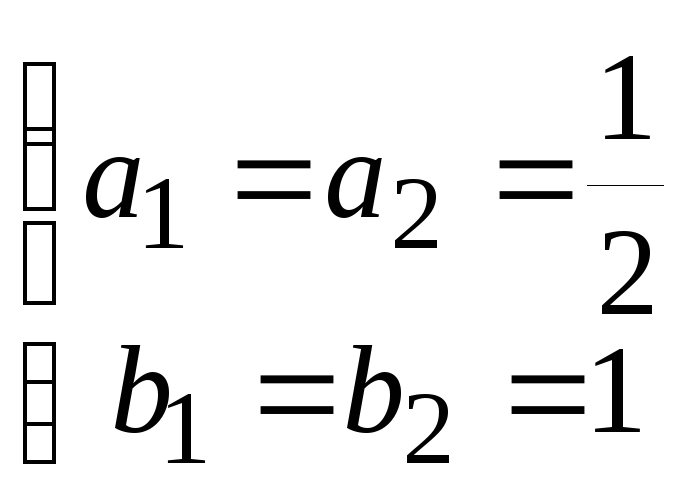а для модифицированного

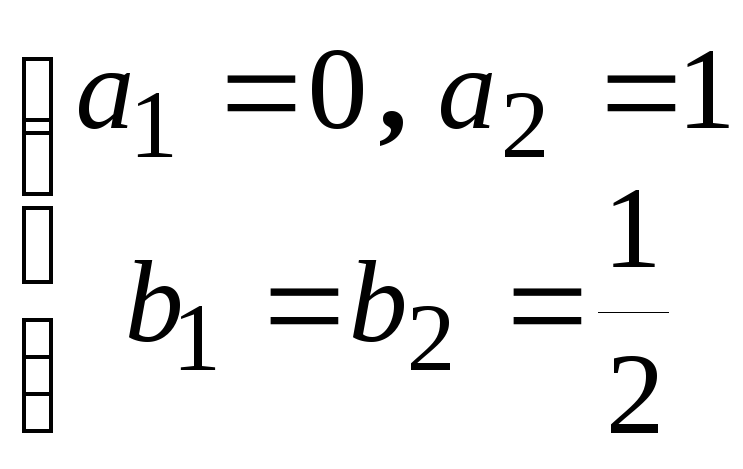
Общая идея вывода формулы метода Рунге-Кутты любого порядка состоит в следующем:

Пусть y(x) –решение дифференциального уравнения y(x)=f(x,y(x)), удовлетворяющее условию y(x_n)=y_n. Проинтегрируем уравнение y(x)=f(x,y) на промежутке по x[x_n,x_n+1], получим :

,

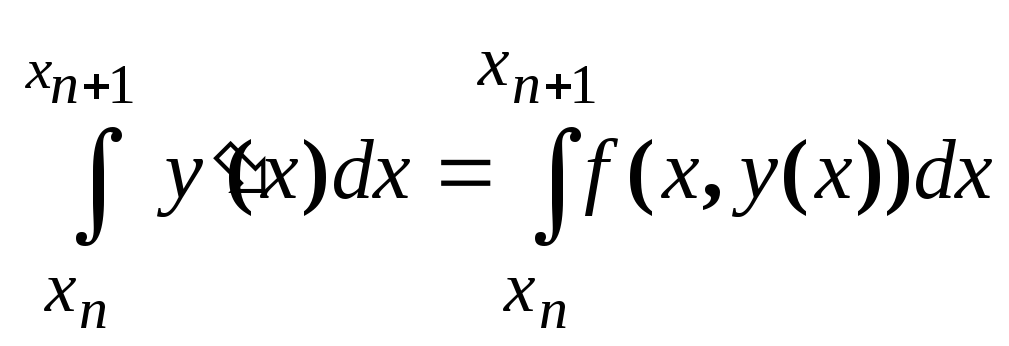по формуле Ньютона-Лейбница .

Тогда

Если бы интеграл в формуле вычислялся точно , то она была бы основной рабочей формулой всех методов численного интегрирования дифференциальных уравнений.

В действительности используют приближенную формулу , заменяя определенный интеграл квадратурной суммой.

На отрезке [x_n,x_n+1] вводят m вспомогательных узлов , где 0=a₁a₂a₃…a_m1 .

Тогда интеграл можно заменить квадратурной суммой

Здесь неизвестны .

Применяя (5.2) , получим 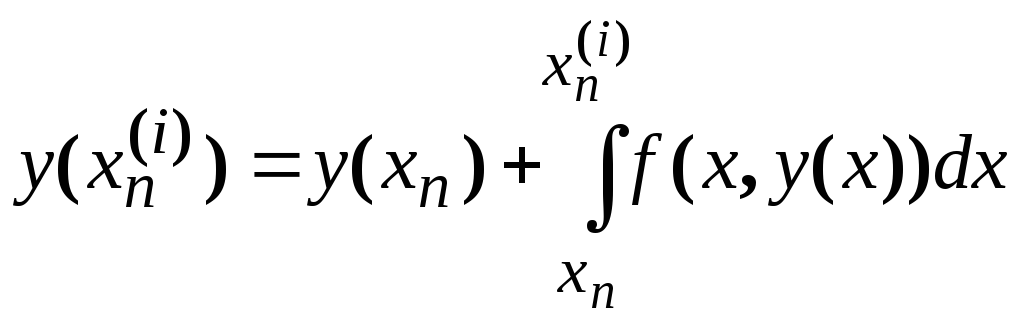, где i=2,3,…,m

Заменив для каждого i интеграл квадратурной суммой и выполнив необходимые преобразования , получим :

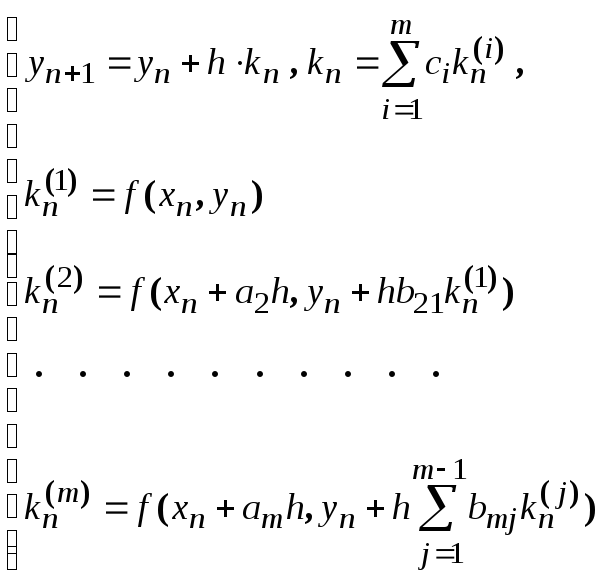
Выбор конкретных значений c_i, a_i и b_i осуществляется по-разному и дает ту или иную модификацию метода Рунге-Кутты.

Приведем рабочие формулы метода четвертого порядка , который применяется настолько широко , что в литературе называется просто «методом Рунге-Кутты» без всяких указаний на тип или порядок.

Классический метод Рунге-Кутты описывается системой следующих шести уравнений:

Геометрический смысл использования метода Рунге-Кутта :

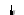1. Из точки M_i с координатами (x_i,y_i) строят касательную в направлении , определяемым углом α₁ , для которого tg α₁=f(x_i,y_i) и находят точку A.

Расстояние NA будет k₁= hf(x_i,y_i).

2. При x=x_i+h/2 в точке F вычисляют наклон второй касательной с углом α₂(касательная показана утолщенным отрезком) tg α₂=f(x_i+h/2,y_i+k₁/2). С этим наклоном проводят прямую из точки M_i и получают точку B .

При этом приращение будет NB k₂=hf(x_i+h/2,y_i+k₁/2).

3. Также при x=x_i+h/2, но уже в точке G пересечения прямой M_i B с одной из кривых семейства, вычисляют ее наклон (касательная показана утолщенным отрезком) как tgα₃=f(x_i+h/2 , y_i+k₂/2). С этим наклоном проводят прямую из точки M_i и на длине шага h получают приращение NC, равное k₃=hf(x_i+h/2,y_i+k₂/2).

Второй и третий этапы представляют не что иное, как модифицированные методы Эйлера.

4. При x=x_i+1 в точке С пересечения прямой M_iC с одной из кривых семейства вычисляют ее наклон (касательная также показана утолщенным отрезком) как tgα₄=f(x_i+h , y_i+k₃) . С этим наклоном проводят прямую из точки M_i и на длине шага h получают приращение ND , равное k₄=hf(x_i+h,y_i+k₃).

5. Окончательно приращение ординаты точки M_i+1 вычисляют как средневзвешенную величину приращений k₁, k₂, k₃, k₄ , с весовыми коэффициентами соответственно

Где k₁= hf(x_i,y_i).

k₂=hf(x_i+h/2,y_i+k₁/2).

k₃=hf(x_i+h/2,y_i+k₂/2).

k₄=hf(x_i+h,y_i+k₃).

Ошибка метода =O(h⁵) , при его использовании необходимо вычислять функцию четырежды.

Ошибки метода Рунге-Кутты.

Для оценки ошибки интегрирования используется принцип Рунге .

Пусть есть точное решение ДУ при .

Тогда для метода Рунге-Кутты справедлива оценка погрешности

Здесь - приближение к точному решению , вычисленное с шагом h/2 - приближение , вычисленное с шагом h.

Для метода p=4 , тогда ошибка интегрирования :

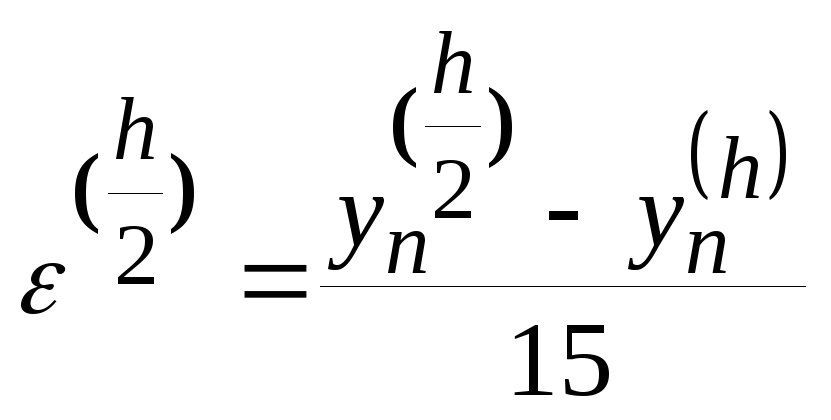
Формула выведена в предположении , что на каждом шаге интегрирования допускается погрешность , приблизительно пропорциональная h⁵, что справедливо для достаточно гладких функций и y⁽⁵⁾(x) у таких функций практически постоянна.

Это довольно точная оценка , однако при ее использовании необходимо вычислять решение два раза.

Предложено несколько полуэмпирических критериев смены шага и выбора оптимального шага интегрирования при условии достижения заданной точности.

Например , используется такое оценочное правило :

если 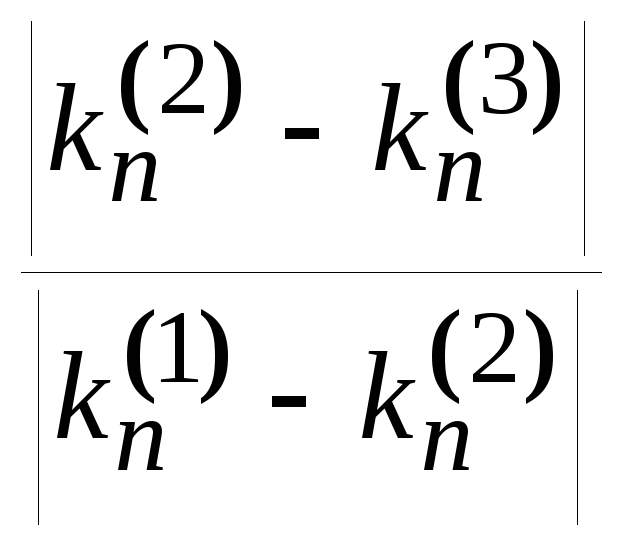достаточно велико (больше нескольких сотых ), то шаг интегрирования необходимо уменьшить .

Рассмотрим пример из лекции 4 :

Рассмотрим Задачу Коши

Пусть шаг h=0,1

Согласно формуле метода имеем:

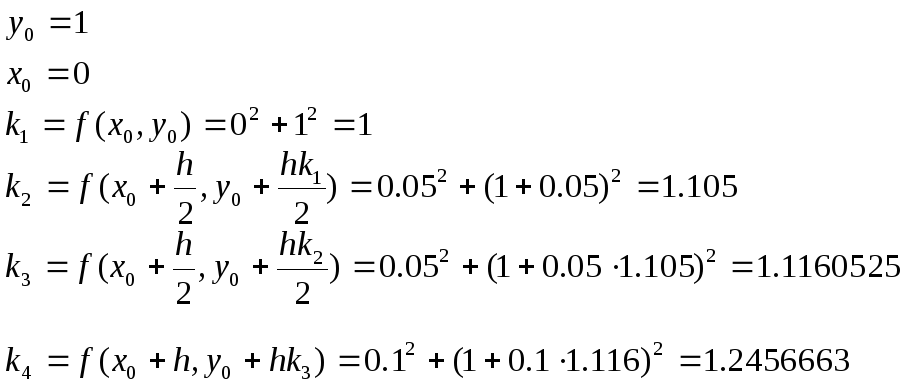
Теперь найдем значение для y₂ :

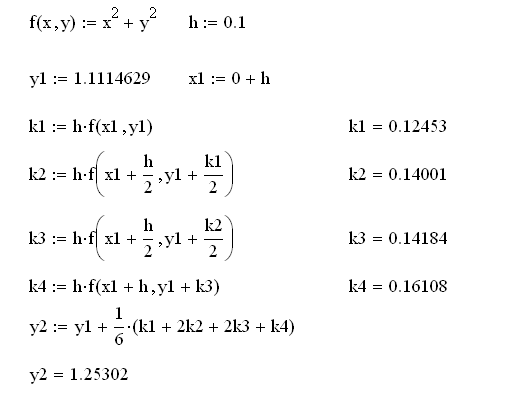
Задача Коши для системы ДУ.

Определение :

Система дифференциальных уравнений называется нормальной , если все уравнения системы разрешены относительно старшей производной .

Рассмотрим систему ДУ вида :

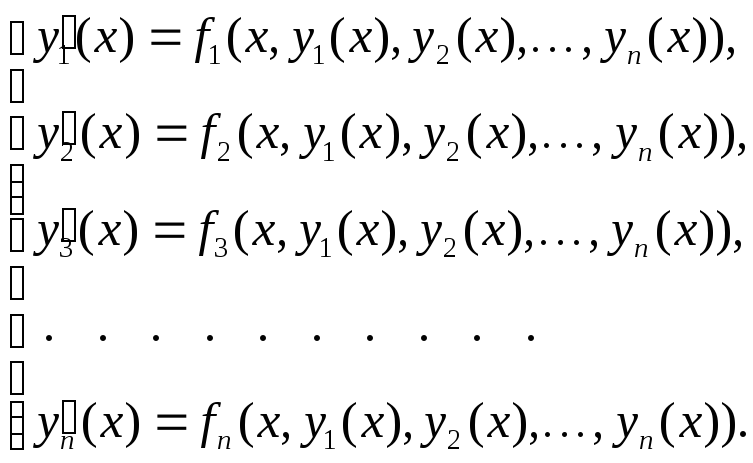
- искомые функции на промежутке [x₀,X]

Заданы начальные условия :

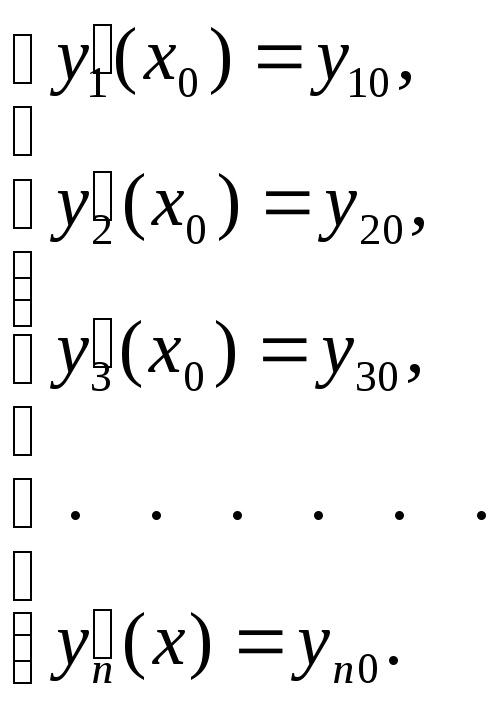
Введем понятие вектор-функции :

, ,

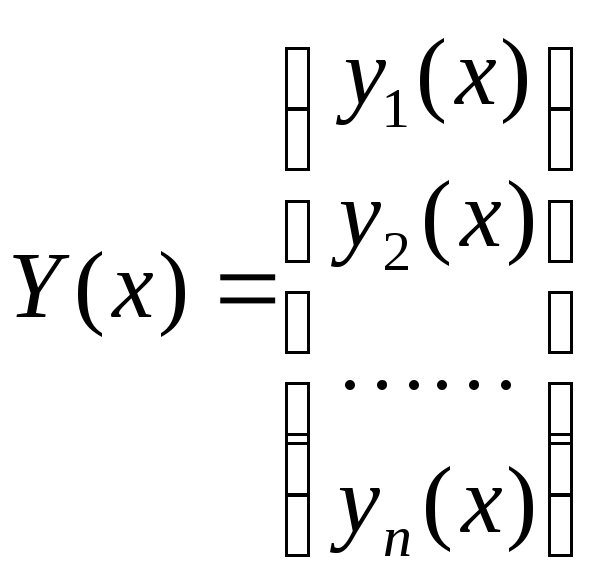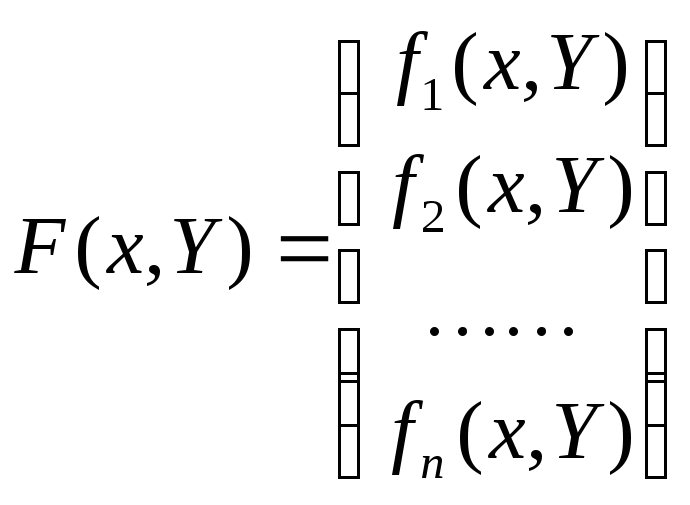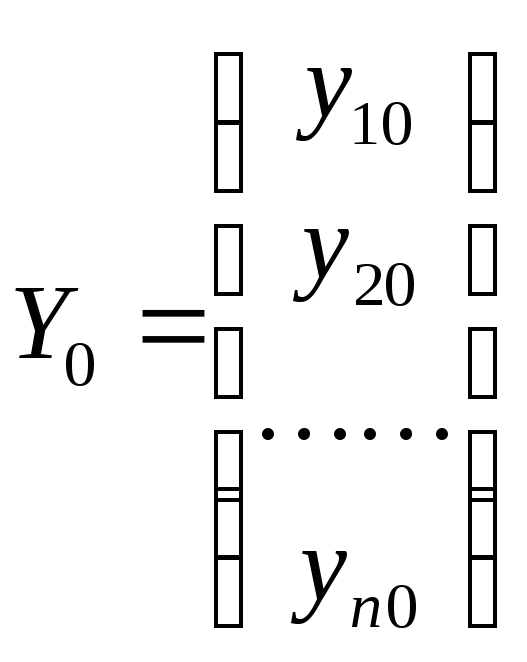
Тогда имеем :

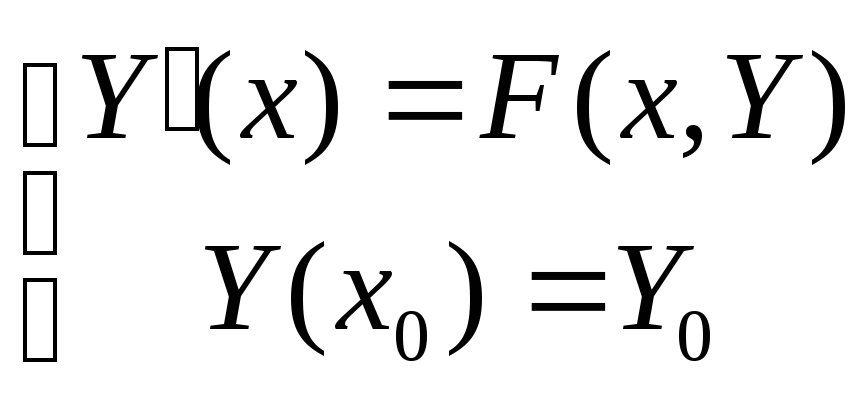
Теорема существования и единственности решения СДУ :

Пусть вектор-функция F(x,Y) определена и непрерывна в области G_x и удовлетворяет условию Липшица

.

Тогда для каждого начального значения Y₀ существует единственное решение Y(x) задачи Коши , определенное на отрезке

Таким образом , решение СДУ методом Эйлера будет иметь вид:

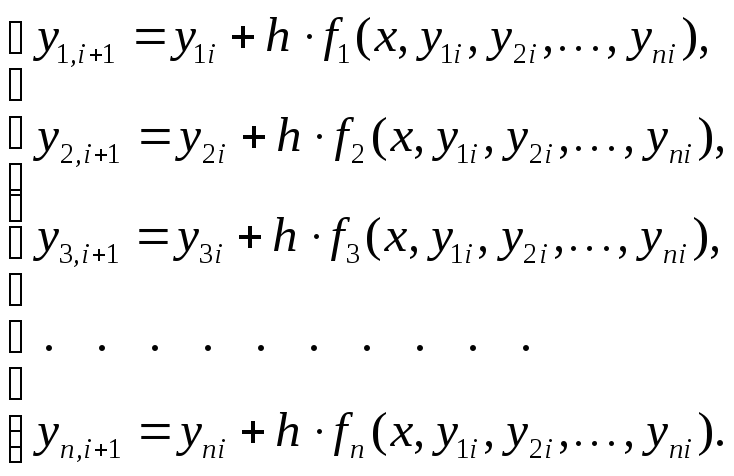
Метод Рунге-Кутты будет иметь вид :

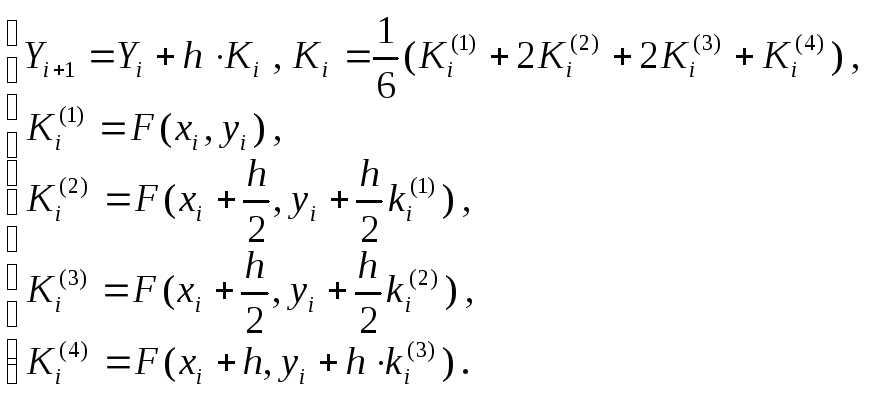
На практике методы решения задачи Коши для одного уравнения первого порядка можно использовать и для решения систем , причем следует лишь заменить в расчетных формулах числа y_i на векторы , а функцию f на вектор-функцию.

8

стр. 8 из 8