13.3. Хід розрахунків

1. Вирахувати значення X-координати точок перетину горизонталей з лініями координатної сітки напрямку OX. Горизонталі будуються з висотою перерізу рельєфу 1 м. Слід мати на увазі, що різні колонки таблиці містять різну кількість чисел. Ця кількість дорівнює кількості цілих чисел, які містяться між значеннями висот у сусідніх вузлах . Результати розрахунків представити у вигляді наступних десяти таблиць (кожна таблиця відповідає рядку матриці висот)

Ряд 1

1 – 2 H X	2 – 3 H X	3 – 4 H X		9 – 10 H X
1.5 9.2	5.4	… …		… …

Ряд 2 ... і т.п. (всього десять таблиць).

Для розрахунків використати формулу

Тут X – шукана координата точки перетину, a – відстань між вузлами (за умовою a=10м), H₁, H₂ – висоти двох сусідніх вузлів, H₀ – цілочисельне значення висоти горизонталі, причому або ж . В окремих випадках, якщо цілі частини чисел і однакові, будемо вважати, що інтервал не перетинає жодна горизонталь.

2. Вирахувати значення Y-координати точок перетину горизонталей з лініями координатної сітки напрямку OY. Горизонталі будуються з висотою перерізу рельєфу 1м. Результати розрахунків представити у вигляді наступних десяти таблиць (кожна таблиця відповідає стовпцю матриці висот)

Стовпець 1

1 – 2 H Y	2 – 3 H Y	3 – 4 H Y		9 – 10 H Y
3.5 6.8	3.6 … …	… …		… …

Стовпець 2 і т.п. (всього десять таблиць).

Для розрахунків використати формулу

Тут Y – шукана координата точки перетину, a – відстань між вузлами (за умовою a=10м), H₁,H₂ – висоти двох сусідніх вузлів, H₀ – цілочисельне значення висоти горизонталі, причому або ж . В окремих випадках, якщо цілі частини чисел і однакові, будемо вважати, що інтервал не перетинає жодна горизонталь.

2. Сполучаючи сусідні точки перетину координатної сітки однакової висоти, отримуємо горизонталі у вигляді ламаних ліній. На міліметровому папері виконуємо рисунок, дотримуючись масштабу 1 : 500.

13.4. Побудова діаграми ухилів

1. Використовуючи задані значення висот у вузлах регулярної мережі розрахуємо значення ухилу для східного, південного, західного, північного, а також чотирьох проміжних напрямків у вузлі 55. Для розрахунків використовуються формули

. ( 2 )

Для вузла 22 з нашого прикладу ухил в північному напрямі визначається так:

.

Аналогічно для східного, південного та західного напрямів маємо:

Розрахункові формули для проміжних напрямків відрізняються від наведених вище тим, що значення знаменника становить . Результати розрахунків оформляємо у вигляді наступної таблиці

Таблиця 1. Розрахунок ухилів для вузла 22.

0.120	0.100	-0.050
0.070		-0.130
-0.100	-0.240	-0.180

2. Розрахуємо напрямки нульового ухилу, використовуючи дані Таблиці 1 і метод лінійної інтерполяції. Після цього будуємо діаграму ухилів.

Діаграма являє собою квадрат, розділений на дві області (інколи на чотири області): область додатних ухилів та область від’ємних ухилів. Для розрахунку напрямків нульового ухилу використовують лінійну інтерполяцію.

Н

Рис. 3. Діаграма ухилів.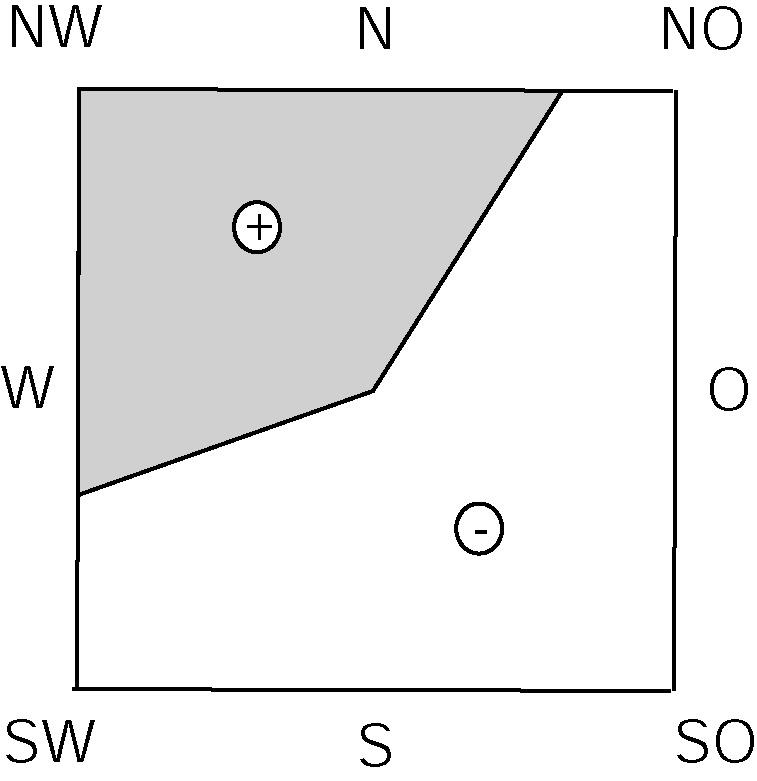

априклад, для північного напряму маємо додатній ухил, для північно-східного – від’ємний. Отже між цими напрямками і знаходиться напрямок нульового ухилу. Складаємо пропорцію між кутовими величинами в градусах та відповідними їм ухилами: . Звідси знаходимо - кутову відстань нульового ухилу від північного меридіана, відраховану за ходом годинникової стрілки. Другий напрям нульового ухилу знаходиться між західним та південно-західним напрямками і розраховується аналогічно.