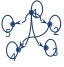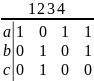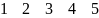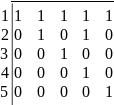ЛАБОРАТОРНАЯ РАБОТА № 2
Бинарные отношения
Цель работы
Познакомиться с понятиями бинарных отношений, изучить способы их представления и свойства, научиться выполнять операции над отношениями.
Теоретические сведения
Отношение
используется как термин для обозначения
связи между предметами или понятиями
( ,
,
 ).
Несмотря на свое широкое применение,
понятие «отношение » имеет строгое
математическое определение.
).
Несмотря на свое широкое применение,
понятие «отношение » имеет строгое
математическое определение.
Основные определения
Пусть
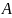 и
и
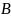 — произвольные множества. Неупорядоченная
пара
на множествах
и
— это любое множество
— произвольные множества. Неупорядоченная
пара
на множествах
и
— это любое множество
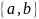 ,
где
,
где
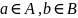 или
или
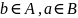 .
Упорядоченная
пара
на множествах
и
,
обозначаемая записью
.
Упорядоченная
пара
на множествах
и
,
обозначаемая записью
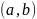 ,
определяется не только самими элементами
,
но и порядком, в котором они записаны.
,
определяется не только самими элементами
,
но и порядком, в котором они записаны.
Простейший
и важнейший пример использования
упорядоченных пар дает аналитическая
геометрия. Если на плоскости введена
некоторая прямоугольная система
координат, то каждая точка плоскости
однозначно задается упорядоченной
парой действительных чисел — координатами
этой точки. Ни у кого не возникает
сомнений в том, что порядок, в котором
перечисляются координаты точки, является
существенным: точка, заданная координатами
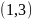 ,
совсем не то же самое, что и точка с
координатами
,
совсем не то же самое, что и точка с
координатами
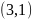 .
.
Множество
всех упорядоченных пар на множествах
и
называют декартовым
(прямым) произведением множеств
и
и обозначают
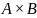 .
Таким образом,
.
Таким образом,
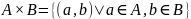 .
.
Если
множества
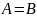 равны между собой, то указанное декартово
произведение называют второй
степенью множества
(или квадратом множества
)и
обозначают
равны между собой, то указанное декартово
произведение называют второй
степенью множества
(или квадратом множества
)и
обозначают
 .
.
Бинарное
отношение
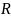 определяют
как подмножество в декартовом произведении
Х × Y, задаваемое определяющим свойством
отношения
.
Если
такое отношение, что
определяют
как подмножество в декартовом произведении
Х × Y, задаваемое определяющим свойством
отношения
.
Если
такое отношение, что
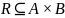 ,
то говорят, что
есть отношение из
в
.
Если
,
то говорят, что
есть отношение
на множестве
.
,
то говорят, что
есть отношение из
в
.
Если
,
то говорят, что
есть отношение
на множестве
.
Представление отношений
Бинарные отношения можно представлять различными способами: перечислением пар, ориентированным графом (графом соответствия), графиком на координатной плоскости, функцией, матрицей отношения (смежности).
Пример
1.
Пусть
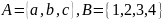 .
Отношение между множествами
и
может быть записано в явном виде:
.
Отношение между множествами
и
может быть записано в явном виде:
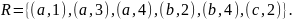
Пример
2.
Пусть
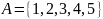 .
Тогда
.
Тогда
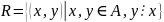 может быть записано в явном виде:
может быть записано в явном виде:

Для
наглядного изображения соответствий
из
и
(бинарных отношений, в частности) будем
использовать два способа. Первый из
этих способов состоит в интерпретации
соответствия как подмножества декартова
произведения, которое можно изображать
примерно так же, как на плоскости можно
изображать подмножества декартова
квадрата числовых множеств. Второй
способ, применяемый для конечных множеств
и
,
— построение так называемого графа
соответствия. В этом случае элементы
множеств
и
изображаются на плоскости кружочками.
Если и только если пара
принадлежит соответствию
,
то в графе соответствия из кружочка,
обозначающего элемент
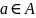 ,
проводим стрелку к кружочку, обозначающему
элемент
,
проводим стрелку к кружочку, обозначающему
элемент
 .
Для бинарного отношения на конечном
множестве
часто удобнее использовать граф другого
вида. Элементы множества А изображаются
кружочками только один раз, а стрелки
проводятся по тем же правилам, что и в
графе соответствия. Заметим, что при
таком построении возможно соединение
кружочка стрелкой с самим собой (петля).
.
Для бинарного отношения на конечном
множестве
часто удобнее использовать граф другого
вида. Элементы множества А изображаются
кружочками только один раз, а стрелки
проводятся по тем же правилам, что и в
графе соответствия. Заметим, что при
таком построении возможно соединение
кружочка стрелкой с самим собой (петля).
a
b c
|
|
||
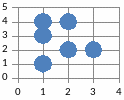
График (пример1) |
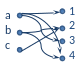
Граф (пример1) |
||
|
|
|
|
график (пример2) |
граф (пример2) |
граф (пример2) |
|
Рис. 1 |
|||
Пусть
есть отношение на
,
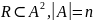 .
Перенумеруем элементы множества
,
.
Перенумеруем элементы множества
,
 .
Тогда отношение
можно представить булевой матрицей
.
Тогда отношение
можно представить булевой матрицей
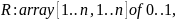 где
где
 .
Понятие «булева матрица» подразумевает,
что элементы матрицы – булевские
значения и операции над ними выполняются
по соответствующим правилам. Матрицы
отношений, рассмотренных в примерах
будут
выглядеть:
.
Понятие «булева матрица» подразумевает,
что элементы матрицы – булевские
значения и операции над ними выполняются
по соответствующим правилам. Матрицы
отношений, рассмотренных в примерах
будут
выглядеть:
|
|
Пример1 |
Пример2 |
Свойства бинарных отношений
Отношение называется:
рефлексивным, если
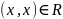 ;
антирефлексивным, если
;
антирефлексивным, если
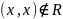 ;
;симметричным, если
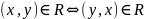 ;
антисимметричным, если
;
антисимметричным, если
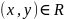 и
и
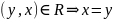 ;
асимметричным, если
;
асимметричным, если
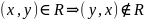 ;
;
транзитивным, если
 ;
;линейным, если
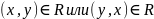 .
.
Из множества всех отношений выделяется класс отношений, одновременно симметричных, транзитивных и рефлексивных. Такие отношения называются отношениями эквивалентности.
К отношениям порядка относятся:
а) отношение квазипорядка, обладающее свойствами рефлексивности, транзитивности;
б)
отношение частичного
порядка
на множестве Х (часто обозначаемое
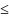 или
или
 ),
обладающее свойствами рефлексивности,
антисимметричности, транзитивности;
),
обладающее свойствами рефлексивности,
антисимметричности, транзитивности;
в)
отношение строгого
порядка
на множестве Х (часто обозначаемое
 или
),
обладающее свойствами антирефлексивности,
асимметричности, транзитивности;
или
),
обладающее свойствами антирефлексивности,
асимметричности, транзитивности;
г) отношение линейного (полного) порядка, обладающее наряду со свойствами отношения частичного порядка свойством линейности.
Функция и отображение
Пусть
– отношение из
в
такое, что
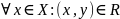 и
и
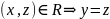 (символ ∀ означает “любой”). Такое
свойство отношения называется
функциональностью,
или однозначностью. Само отношение
называется отображением
из
в
,
или функцией,
и обозначается
(символ ∀ означает “любой”). Такое
свойство отношения называется
функциональностью,
или однозначностью. Само отношение
называется отображением
из
в
,
или функцией,
и обозначается
 или
или
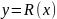 ,
где
,
где
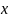 – аргумент,
– аргумент,
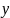 – значение функции.
– значение функции.
Отображение
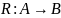 называют инъективным
(инъекцией),
если каждый элемент из области его
значений имеет единственный прообраз,
т.е. из
называют инъективным
(инъекцией),
если каждый элемент из области его
значений имеет единственный прообраз,
т.е. из
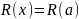 следует
следует
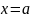 .
Инъективное отображение из
в
называют также отображением
множества
в
множество
.
.
Инъективное отображение из
в
называют также отображением
множества
в
множество
.
Отображение называют сюръективным (сюръекцией), если его область значений совпадает со всем множеством . Сюръективное отображение из в называют также отображением множества на множество .
Отображение называют биективным (биекцией), если оно одновременно инъективно и сюръективно.
Таким образом, если отображение биективно, то каждому элементу множества отвечает единственный элемент множества и наоборот. В таком случае говорят, что множества и находятся между собой во взаимно однозначном соответствии. Биекцию множества на себя называют автоморфизмом множества . Используют также термин “подстановка множества”.
Операции над отношениями
Поскольку отношения можно считать множествами, то все операции над множествами (пересечение, объединение, разность, дополнение и т.д.) можно применить и к отношениям. Заметим, что, говоря о дополнении отношения из в , мы имеем в виду дополнение до универсального отношения из в , т.е. до декартова произведения . Естественно, что и равенство отношений можно трактовать как равенство множеств. В то же время на отношения можно распространить операции, определяемые для отображений. Рассмотрим такие операции.
Композицией
(произведением)
отношений
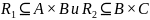 называют отношение
называют отношение
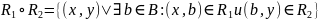 .
.
Поясним
построение композиции двух соответствий.
Обратимся сначала к отображениям (как
частным случаям отношений). Пусть заданы
отображения:
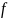 из
в
и
из
в
и
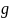 из
в
из
в
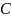 .
Композиция
.
Композиция
 определяется как отображение из
в
,
задаваемое формулой
определяется как отображение из
в
,
задаваемое формулой
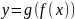 .
Тем самым задается график отображения
,
т.е. множество упорядоченных пар
.
Тем самым задается график отображения
,
т.е. множество упорядоченных пар
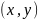 ,
таких, что
.
При этом упорядоченная пара
будет принадлежать графику отображения
,
если и только если найдется элемент
,
такой, что
,
таких, что
.
При этом упорядоченная пара
будет принадлежать графику отображения
,
если и только если найдется элемент
,
такой, что
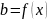 и
и
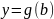 .
.
Вернемся
к рассмотрению композиции отношений
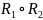 .
Полагая, что область определения
.
Полагая, что область определения
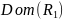 отношения
отношения
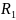 не пуста, возьмем произвольный элемент
не пуста, возьмем произвольный элемент
 .
Пусть сечение
.
Пусть сечение
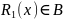 отношения
не пусто и найдется такой элемент
отношения
не пусто и найдется такой элемент
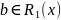 ,
что сечение
,
что сечение
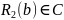 также не пусто. Тогда непустое множество
также не пусто. Тогда непустое множество
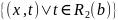 будет подмножеством сечения отношения
в точке
.
Сечением
отношения
в точке
будет непустое в силу сделанных
предположений множество всех таких
упорядоченных пар
будет подмножеством сечения отношения
в точке
.
Сечением
отношения
в точке
будет непустое в силу сделанных
предположений множество всех таких
упорядоченных пар
 ,
что
,
a
,
что
,
a
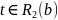 для некоторого
.
Говоря неформально, нужно перебрать
все элементы
для некоторого
.
Говоря неформально, нужно перебрать
все элементы
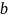 из сечения
из сечения
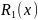 .
Таким образом, различие в построении
композиции отношений и композиции
отображений заключается в том, что
„промежуточный" элемент
в общем случае не единственный и каждому
такому элементу также ставится в
соответствие не единственный элемент
.
Таким образом, различие в построении
композиции отношений и композиции
отображений заключается в том, что
„промежуточный" элемент
в общем случае не единственный и каждому
такому элементу также ставится в
соответствие не единственный элемент
 .
.
Пример
3.
Зададим на множестве
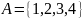 бинарные отношения
бинарные отношения
 ,
и
,
и
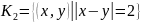 и найдем композицию
.
и найдем композицию
.
Имеем
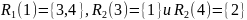 .
Следовательно,
.
Следовательно,
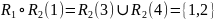 .
Далее
.
Далее
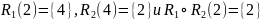 .
Так как
.
Так как
 ,
то в итоге получим
,
то в итоге получим
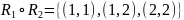 .
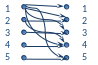
Построение композиции проиллюстрировано
на рис. 2a.
.
Построение композиции проиллюстрировано
на рис. 2a.
|
|
|
|
a) |
b) |
||
Рис. 2 |
|||
Подобным
образом можно построить композицию
отношений
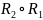 ,
что отображено на рис. 2b.
Легко видеть, что
,
что отображено на рис. 2b.
Легко видеть, что
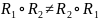 .
.
Пусть
— бинарное отношение. Определим обратное
отношение
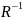 следующим образом:
следующим образом:
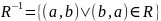 .
.
Таким образом, связывает те же пары элементов, что и , но «в другом порядке».