3.2 Средньоквадратичний підхід. Eфективності оцінок

Нехай ХІ,..., Хп вьіборка обгема п з параметричного сімейства розподілів, _ де  є .

Визначення 8. Кажуть, що оцінка ₁ краще за оцінку ₂ в смислі середньоквадратичного підходу, якщо для будь-кого  є 

й хоч би при одному  ця нерівність строга.

Оцінки можуть бути непорівнювані: наприклад, при деяких  Е (* - )²  Е (₂^* - )², при інших  - навпаки.

Чи Існує серед всіх оцінок найкраща в смислі середньоквадратичного підходу? Скептик зі схильністю до філософії відразу відповість «немає». Доведемо, що він правий.

Теорема 6. У класі всіх можливих оцінок найкращої оцінки в смислі среднеквадратического підходу не існує.

Доказ теореми 6. Пусть, навпаки, * найкраща, то єсть для будь-який інший оцінки ?, при будь-якому  є 

Нехай 1 довільна точка . Роздивимось оцінку (статистику) *1 = 1. Тоді

при будь-якому  є . Візьмем  = 1 є  і отримаємо наступну нерівність:

тому Е1 (* - 1)^{2 =} 0. Внаслідок довільності 1 це виконується при будь-якому  є :

Але зто можливо тільки якщо * =  (оцінка в точності відгадує невідомий параметр). Тобто * навіть не є статистикою. Такого типа приклади привести можна, але математичній статистиці тут робити нічого.

Вправа. Обгясніть словесно доказ теоремьі 6.

Якщо в дуже широкому класі всіх оцінок якнайкращої не існує, то, можливо, слід звузити клас рассматриваемьіх оцінок (або розбити клас всіх оцінок на окремі підкласи й в кожному шукати якнайкращу).

Як правило розглядають оцінки, що мають однаковий зсув b()= Е_* — . Позначимо через К класе оцінок, що мають зсув Ь(в\.

Тут До — класі незміщенних оцінок.

Визначення 9. Оцінка * є Кь називається еффективною оцінкою в класі Кь, якщо вона краще (не гірше) всіх інших оцінок класа_Кь в смислі середньоквадратичного підходу. Тобто для будь-кого * є Кь для будь-кого  є 

Визначення 10. Зффективна оцінка в класі К₀ (незміщенних оцінок) називається просто зффективною.

Зауваження 10. Для * є К_b, за визначенням дисперсії, Е_(* - ) ² = Е (* - Е*)² =D*,так що порівняння в середньоквадратичному несмещенньїх оцінок — зто порівняння їх дисперсії. Тому еффективну оцінку (в класі К₀) часто називають «незміщеною оцінкою з рівномірно мінімальною дисперсією». Рівномірність мається на увазі по всіх  є . Для * є К_b

отже порівняння в середньоквадратичному оцінок з одинаковим зсувом — це також порівняння їх дисперсії.

Вправа. Ми збираємося шукати якнайкращу оцінку в класі Кь. Обясніть, чому доказ теореми 4 не пройде в класі Кь.

3.3 Єдиність еффективної оцінки в класі з фіксованим зсувом

Теорема 7. Якщо ₁* є Кь і ₂^* є Кь — дві еффективні оцінки в класі Кь, то з вірогідністю 1 вони співпадають: Рд(₁* = ₂^*)= 1.

Доказ теореми 7. Закиданням спочатку, що Е (* - ) ² = Е (2* - )². Дійсно, оскільки 1* еффективна в класі Кь, то вона не гірше за оцінку 2*, тобто

і навпаки. Тому Е (1* - ) ² = Е (2* - ) ^2.

Розглянемо оцінку (довести!). Вичислим її средньоквадратичне відхилення.

Помітимо, що

Покладемо а = в* - 9, Ь = 9% - 9. Тоді (а + Ь) /2 = 9* - 9, а - Ь = в* - 9%. Підставимо ці вирази в (4) й візьмемо математичні очікування обох частин:

Але оцінка * належить Кb, тобто вона не краща, наприклад, еффективної оцінки *. тому

Порівнюючи цю нерівність з рівністю (5), бачимо, що

Тоді (чому?) Р (₁* = ₂^*)= 1, що й було потрібне довести.

Для прикладу розглянемо порівняння двох оцінок. Зрозуміло, порівнюючи оцінки попарно між собою, якнайкращої оцінки в цілому класі не знайти, але вибрати кращу з двох теж корисно. А способами пошуку як найкращої в цілому класі теж скоро займемося.

Приклад 10. Хай ХІ..., Хп — вибірка обєму п з рівномірного розподілу Uо, , де  > 0.Тоді  = Х(n)= mах{ХІ...,Хп} — оцінка максимальної правдоподібності, а * = 2Х — оцінка методу моментів, одержана по першому моменту. Порівняємо їх в середньоквадратичному. Оцінка * = 2Хнезміщена (див. приклад 4), позтому

Для  = Х(n)= тах{ХІ..., Хп} маємо

Порахуємо перший й другий момент випадкової величини в = Х(п). Знайдемо (корисно пригадати, як це робилося в минулому семестрі!) функцію розподілу й густина :

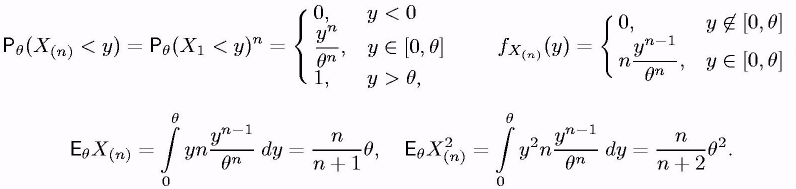
тому

При п = І квадратичні відхилення рівної, а при п > І

то є Х(n) краще, ніж 2Х. При цьому E(X(n)- )²  0 із швидкістю n^-2, тоді як Е (2Х - ) 0 із швидкістю n^-1.

Вправа.

1. Довести, що Х(п) є Кь

2. Довести, що (незміщена).

6. Порівняти оцінки в середньоквадратичному.

3.4 Асимптотика нормальніше оцінки (АНО)

Для того, щоб вміти порівнювати оцінки вигляду (див. приклад 4), среднеквадратического підходу недостатньо: другий момент такої випадкової величини порахувати навряд чи вдасться. Оцінки такого вигляду (функції від сум) вдається порівнювати за допомогою асимптотичного підходу. Більш точно цей підхід застосовний до так називається «асимптотика нормальним» оцінкам.

Хай ХІ..., Хп — виборка обєма п з параметричного сімейства розподілів Уд, в є в.

Визначення 11. Оцінка * називається асимптотично нормальною оцінкою параметра  з коефіцієнтом ²() якщо

Приклад 11. Хай ХІ..., Хп — вибірка обєма п з рівномірного розподілу U0, де  > 0. Перевіримо, чи є оцінки * = 2Х i  = Х(n) асимптотиxно нормальними (АНО). По ЦПТ

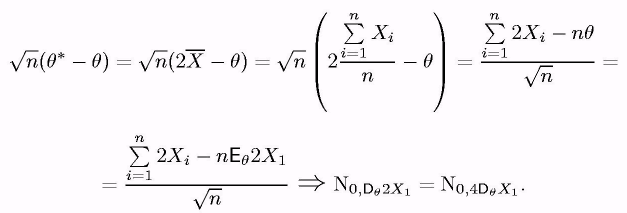
Та оцінка * = 2Х асимптотика нормальна з коефіцієнтом а2(в)= 4С>дХІ = 46>2/12 = 6>2/3. Для оцінки  = Х(n) маємо:

Таким чином, оцінка в = Х(П) асимптотика нормальної не є.

Залишилося відповісти на питання що напрошуються:

1) Куди все ж таки сходиться по розподілу n(X(n)- )? Вправа. Довести, що n(X(n)- )0.

Порядок дій: Виписати визначення слабкої збіжності. Намалювати функцію розподілу нуля. Знайти за визначенням функцію розподілуn(X(n)- )_. Переконатися, що вона сходиться до ф.р. нуля у всіх точках неперервності останньої. Не забудьте про існування замечательних меж, логарифмів й ряду Тейлора.

2) Якщо n(X(n)- )0, то на який ступінь п потрібно спробувати помножити, щоб одержати збіжність до величини, відмінної від 0 й оо?

Вправа. Довести, що n(X(n)- ), причому величина — має показове розподілення Е1/0.

Порядок дій: колишній.

3) Для оцінки властивість (6) не виконано. Чи може ця оцінка бути АНО?

Вправа. Модифікувати міркування й довести, що ця оцінка теж не є асимптотика нормальною.

4) Чи погано, що оцінка  = Х(n) не асимптотика нормальна? Може бьіть, збіжність n(X(n)- ) ще краще?

Попробуєм відповісти на останнє питання.