2.4 Спроможність оцінок методу моментів

Теорема 5. Нехай * = h^-1(Xk) оцінка параметра в, отримана по методу моментів, причому функція h^-1 безперервна. Тоді * спроможна.

Доказ теореми 5.

По лемме 3 маємо: X^k E_X₁^k = h(). Оскільки функція h^-1 безперервна, то і

Зауваження 8. Для оборотної, тобто взаімнооднозначной функції h: R  R безперервність h і безперервність h^-1 еквівалентні.

2.5 Методи знаходження оцінок: метод максимальної правдоподібності

Метод максимальної правдоподібності ще один розумний спосіб побудови оцінки невідомого параметра. Складається він в тому, що як «найбільш правдоподібне» значення параметра беруть значення в, максимизирующее імовірність отримати при n дослідах дану вибірку X = (Х₁,..., Хп). Це значення параметра залежить від вибірки і є шуканою оцінкою.

Вирішимо спочатку, що таке «імовірність отримати дану вибірку», тобто що саме треба максималізувати. Пригадаємо, що для абсолютно безперервних розподілів _ їх щільність f_(у) «майже» (з точністю до dy) імовірність попадання в точку у. А для дискретних розподілів _ імовірність попасти в точку у рівна P_(X₁ = у). І те, і інше ми будемо називати щільністю розподілу _ (відступаючи при цьому, для простоти, від термінології теорії імовірностей). Отже,

Визначення 5. Функцію

ми будемо називати щільністю розподілу F.

Визначення 6. Функція (взагалі кажучи, випадкова величина)

називається функцією правдоподібності. Функція (також випадкова)

називається логарифмічною функцією правдоподібності.

Якщо наша вибірка X в даній серії експериментів прийняла значення (x₁,..., х_n), те (в дискретному випадку) функція правдоподібності і є імовірність цієї події, різна при різних значеннях параметра в:

Визначення 7. Оцінкою максимальної правдоподібності  невідомого параметра  називають значення , при якому функція (Х, ) досягає максимума (як функція від в при фіксованих X₁,..., Х_n):

 = точка максимума (по змінній ) функції (Х, )

Зауваження 9. Оскільки функція ln у монотонна, то точки максимума (X, ) і L(X, ) співпадають. Тому оцінкою максимальної правдоподібності (ОМП) можна називати точку максимума (по в) функції L(х, ):

 = точка максимума (по змінній ) функції L(X, ).

Нагадаємо, що точки экстремума функції це або точки, в яких похідна звертається в нуль, або точки розриву функції/похідного, або крайні точки області визначення функції.

Приклад 6. Нехай Х₁,..., Хп вибірка об'єму п з розподілу Пуассона: X_i  П_, де  > 0. Найдем ОМП А невідомого параметра .

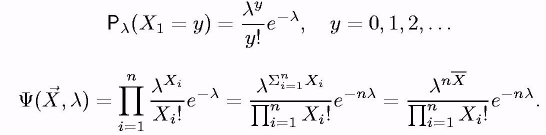
Оскільки ця функція при всіх  > 0 безперервно диференціюється по , можна шукати точки экстремума, прирівнявши до нуля приватну похідну по . Але зручніше це робити для логарифмічної функції правдоподібності:

і точка экстремума  рішення рівняння: , тобто  =X.

Вправа.

1. Пересвідчитися, що  = X точка максимума, а не мінімуму.

2. Пересвідчитися, що  = X співпадає з однією з оцінок методу моментів (по якому моменту?).

Приклад 7. Нехай Х₁,..., Хп вибірка об'єму п з нормального розподілу N_a,2, де а  R,  > 0; і обидва параметри а, ² невідомі.

Випишемо щільність, функцію правдоподібності і логарифмічну функцію правдоподібності. Щільність:

функція правдоподібності:

логарифмічна функція правдоподібності:

У точці экстремума (по (а, 2)) ^{гладкої} функції L звертаються в нуль обидві приватні похідні:

Оцінка максимальної правдоподібності (а, 2) для (а, 2) рішення системи рівнянь

Вирішуючи, дістанемо добре знайомі оцінки:

Вправа.

1. Пересвідчитися, що 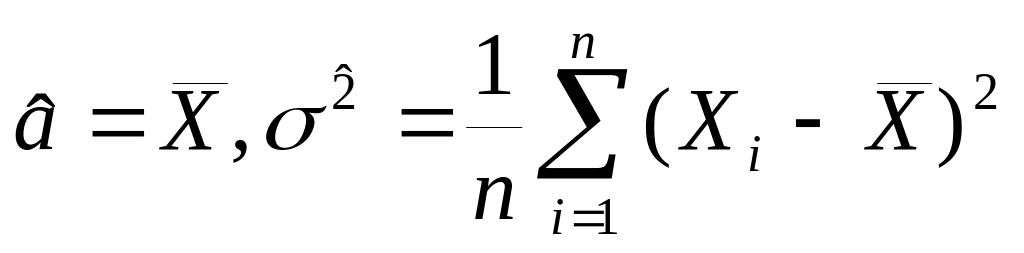точка максимуму, а не мінімуму.

2. Пересвідчитися, що ці оцінки співпадають з деякими оцінками методу моментів.

Приклад 8. Нехай X₁,..., Хп вибірка об'єму п з рівномірного розподілу U_{0,__,} де  > 0. Тогда  = Х(n) ₌ тах{Х₁ ,...,Х_n} (див.)( [1])(, приклад 2.5, c. 10).

Приклад 9. Нехай Х₁,..., Хп вибірка об'єму п з рівномірного розподілу U_,+5, де >0 (див. також [2], приклад 4, с.48).

Випишемо щільність і функцію правдоподібності. Щільність:

функція правдоподібності:

Функція правдоподібності досягає свого максимального значення (1/5)ⁿ у всіх точках   [Х_(n)- 5, X₍₁₎ ]. Графік цієї функції зображений на мал. 9.

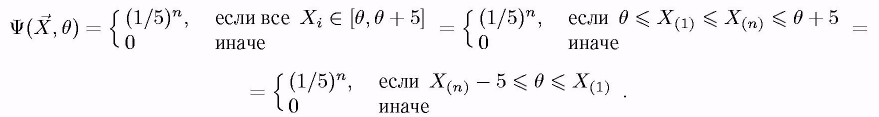
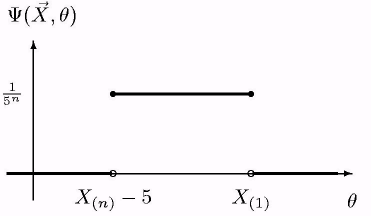
МАЛ. 9: Приклад 9.

Будь-яка точка   [Х_(n) - 5, Х₍₁₎ ] може служити оцінкою максимальної правдоподібності. Отримуємо більш ніж рахункове число оцінок вигляду _ = (1 - )(Х_(n) – 5) + Х₍₁₎, при різних  [0,1], в тому числі ₀ = Х_(n) - 5, ₁ = X₍₁₎ кінці відрізка.

Вправа.

1) Пересвідчитися, що відрізок [Х_(n) - 5, Х₍₁₎ ] не пустий.

2) Знайти оцінку методу моментів (по першому моменту) і пересвідчитися, що вона відрізняється від ОМП.

3. Знайти ОМП параметра  рівномірного розподілу U_,+3 .