1.4 Емпіричні моменти

Знання моментів розподілу також багато чого може сказати про його вид і властивості. Введемо емпіричні (вибіркові) аналоги невідомих теоретичних (істинних) моментів розподілу.

Нехай Е = ЕХ₁ = a, D = DX₁ = ², E = ЕХ₁^k = m_k — теоретичне середнє, дисперсія, k-й момент. Добре відомі їх вибіркові «двійники»:

Коротко визначити зміст правого і лівого стовпців таблиці можна так: невідоме «середнє по просторі» заміняється «середнім за часом» (цитата, група 476).

1.5 Збіжність емпіричних характеристик до теоретичних

Ми ввели три види емпіричних характеристик, призначених для заміни (оцінювання) невідомих теоретичних характеристик розподілу: емпіричну функцію розподілу, гістограму, вибіркові моменти. Зрозуміло, що будь-яке наближення гарне, якщо з ростом обсягу вибірки різниця між істинною характеристикою і вибірковою прагне до нуля. Таку властивість емпіричних характеристик («оцінок») називають здатністю. Переконаємося, що наші вибіркові характеристики такою властивістю володіють.

Властивості емпіричної функції розподілу

Теорема 1. Нехай X = (Х₁,..., Х_п) — вибірка об’єму п з невідомого розподілу F з функцією розподілу F. Нехай F_n^* — емпірична функція розподілу, побудована по цій вибірці. Тоді для кожного у є R

Зауваження 2. F_n^*(y) — випадкова величина, тому що вона є функцією від випадкових величин Х₁,..., Хп. Те ж саме можна сказати про гістограму і вибіркові моменти.

Доведення теореми 1. По визначенню,

Випадкові величини I(Х₁ < у), I(X₂ < у),... незалежні й однаково розподілені, їхнє математичне очікування скіннченно:

тому застосуємо ЗБЧ Хінчіна (а що це таке?), і

Таким чином, з ростом обсягу вибірки емпірична функція розподілу сходиться (по ймовірності) до невідомої теоретичної.

Насправді, вірний більш загальний результат, що показує, що збіжність емпіричної функції розподілу до теоретичного має «рівномірний» характер.

Теорема 2 (Гливенко, Кантеллі). Нехай X = (Х₁,..., Х_п) — вибірка обсягу п з невідомого розподілу У с функцією розподілу F. Нехай F_n^* — емпірична функція розподілу, побудована по цій вибірці. Тоді

Якщо функція розподілу F безупинна, то швидкість збіжності до нуля в теоремі Гливенко- Кантеллі має порядок 1/n, як показує

Теорема З (Колмогоров). Нехай X = (Х₁,...,Х_п) — вибірка обсягу п з невідомого розподілу У з неперервною функцією розподілу F. Нехай F_n^* — емпірична функція розподілу. Тоді

де випадкова величина З має розподіл Колмогорова з функцією розподілу

Випишемо ще ряд властивостей емпіричної функції розподілу, що нам будуть потрібні надалі. Це добре знайомі властивості середнього арифметичного п незалежних доданків, що мають до того ж розподіл Бернуллі.

Властивість 1. Для кожного y R

, тобто величина F_n^*(y) — «незміщена» оцінка для F(y);

І, тобто величина F_n^*(y) «асимптотично нормальна»;

має біноміальний розподіл B_n,F(y).

У перших трьох пунктах стверджується, що випадкова величина F_n^*(y) має математичне очікування

F(y), має убутну зі швидкістю 1/n дисперсію

Гливенко-Кантеллі, сходиться до F(y) зі швидкістю 1/n.

і, на додаток до теореми

Зауваження 3. Корисно порівняти (3) з теоремою Колмогорова.

Зауваження 4. Усі визначення, як те: «оцінка», «незміщеність», «заможність», «асимптотична нормальність» будуть дані в главі 2. Але зміст цих термінів повинний бути цілком зрозумілий уже зараз.

Доказ властивості 1.

1) Випадкові величини I(Х₁ < у), I(Х₂ < у),... однаково розподілені, тому (де використовується однакова распреділеність?)

2) Випадкові величини I(Х₁ < у), 1(Х₂ < у),... незалежні й однаково розподілені, тому (де використовується незалежність?)

Ho di(x <y) = F(y)(1 - F(y)), оскільки І(Х < у) B_F(y).

3) Скористаємося ЦПТ Ляпунова (а що це таке?).

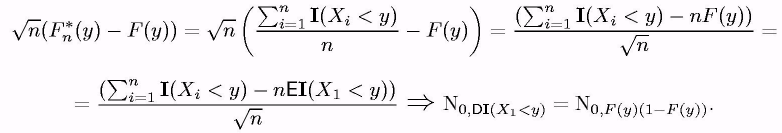
4) Оскільки I(Х₁ < у) (число успіхів в одному іспиті) має розподіл Бернуллі В_F(y) (ще раз - чому?), те п • F_n^*(y) = ⁿ_i=1 I(X₁ < y) біноміальний розподіл В_n,F(y) (чому? і при чому тут зміст біноміального розподілу? а також при чому тут його стійкість по сумуванню?).

Властивості гістограми Нехай  — щира невідома щільність розподілу В (якщо В абсолютно безупинно). Нехай, крім того, число k інтервалів групи не залежить від п. Див. зауваження 5 для випадку, коли k = k(n). Справедлива

Теорема 4. При п   для будь-якого j = 1,..., k

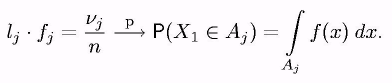
Якщо, до того ж, щира щільність f(x) безупинна на інтервалі a_j , то інтеграл праворуч дорівнює lj • f(uj), де uj - деяка крапка усередині інтервалу угруповання a_j (знайдеться по теоремі про середній).

Вправа. Довести теорему 4, використовуючи (1) і ЗБЧ.

Теорема затверджує, що (для безупинної щільності) висота стовпця гістограмми, побудованого над інтервалом угруповання, з ростом обсягу вибірки зближається зі значенням щільності розподілу в одній із крапок цього інтервалу. Або (для довільної щільності) площа відповідного стовпця гістограмми зближається з площею над тим же інтервалом під графіком щільності.

Вправа. Намалювати твердження теореми 4 на графіку щільності / гістограмми.

Зауваження 5. Помітимо, що чим більше інтервалів угруповання, тим краще. Але це «чим більше» має свої границі: якщо брати число інтервалів, скажемо, порядку п, те з ростом п гістограмма не буде поточечно сходитися до щільності.

Справедливо наступне твердження: якщо щільність розподілу елементів вибірки є безупинною функцією і k(n)/n  0, то має місце поточечна збіжність гістограмми до щільності (див. зауваження 1).

Зі своєї сторони, можу запропонувати завжди брати число інтервалів, скажемо, рівне цілої частини від кореня п'ятого ступеня з п (помноженого на е^, якщо обсяг вибірки більше 413):

Властивості вибіркових моментів

Лема 1. Вибіркове середнє X є незміщеною і заможною оцінкою для теоретичного середніх (математичного чекання):

1. ЕХ = ЕХ₁ = а — незміщеність;

2. X ^p ЕХ₁ = а — заможність.

Лема 2. Вибіркові дисперсії ² і s₀² є заможними оцінками для дисперсії. При цьому ^2* — зміщена, a s₀² — незміщена оцінка дисперсії:

— зміщена;

— незміщена;

— обидві оцінки достовірні.

Лема 3. Вибірковий k-й момент X^k є незміщеною і достовірною оцінкою для теоретичного k-го моменту:

1. EX^k = EX₁^k_ = m_k — незміщеність;

2. X^k ^p EX₁ ^k= m_k при п   — заможність.

Доказ леми 1.

Вправа. Довести лему 3.

Доказ леми 2.

1) У перших, розкривши дужки, корисно переконатися в тім що

Потім,

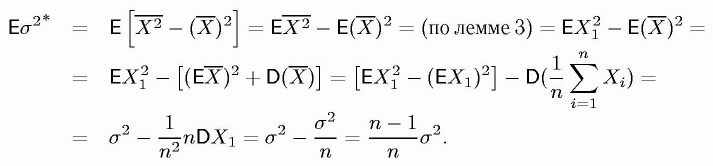
2) Друге твердження випливає з першого, тому що

3) З (2) і ЗБЧ,

Крім того, .

1.6 Згруповані дані (деякі вступні поняття до економетрії)

Якщо обсяг вибірки дуже великий, часто працюють не з елементами вибірки, а з групованими даними. Приведемо ряд понять, зв'язаних з угрупованням. Для простоти будемо поділяти область вибіркових даних на k однакових інтервалів А₁,..., A_k довжини А:

Як колись, нехай Vj — число елементів вибірки, що потрапили в інтервал a_j і _j — частота влучення в інтервал a (оцінка імовірності влучення в інтервал):

На кожнім з інтервалів a_j будують прямокутник з висотою , і одержують гістограмму.

Розглянемо середини інтервалів: a_j = а_j-1 + /2 — середина a_j. Набір

можна вважати «огрубленою» вибіркою, у якій усі Х_i, що попадають в інтервал a_j, замінені на a_j. По цій вибірці можна побудувати такі ж (але більш грубі) вибіркові характеристики, що і по вихідній (позначимо їхній так само), наприклад вибіркове середнє

чи вибіркову дисперсію

Вправа.

1) Знайти математичне чекання і дисперсію випадкової величини, що приймає значення a₁,..., a_k

с імовірностями, відповідно, ₁, . . . , _k.

2) Знайти математичне чекання і дисперсію випадкової величини, що приймає значення X₁,..., Х_п із рівними імовірностями.

Вправа.** Зрозуміти, до чого попередня вправа.

Указівка. Обґрунтувати фразу: вибіркові характеристики (вибіркове середнє, вибіркова дисперсія, вибіркова функція розподілу, вибірковий k-й момент і ін.) є звичайні характеристики (математичне чекання, дисперсія, функція розподілу, k-й момент і т.д.) вибіркової випадкової величини, що приймає значення Х_,..., Х_п із рівними імовірностями.

Крива, що з'єднує крапки (а₀ , 0) , (а₀ , f₁) , ... , (а₀ , f_k) , (а_k , 0) називається полігоном (частот). На відміну від гістограмми полігон — безупинна функція (ламана).