4.3 Макроскопическая работа как функция процесса

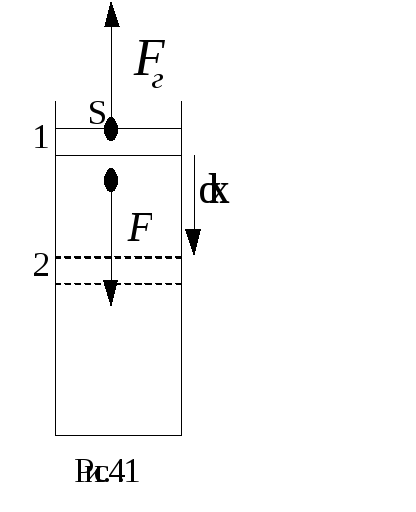
Рассмотрим сжатие идеального газа, находящегося под поршнем (рис. 4.1). Под действием внешней силы переместим поршень на бесконечно малую величину , настолько малую, что будем считать силу постоянной. Назовём работу постоянной силы по перемещению поршня на бесконечно малую величину элементарной работой и обозначим . Элементарная работа может быть определена как работа постоянной силы через скалярное произведение силы на перемещение:

(4.6)

Поскольку направление силы и перемещения совпадают, то . Газ, находящийся под поршнем, препятствует сжатию и давит на поршень силой , равной по величине, противоположной по направлению и приложенной к поршню (рис.4.1). Элементарная работа самого газа . Так как сила и перемещение направлены в противоположные стороны, работа самого газа при равномерном сжатии отрицательна и равна по величине работе внешней силы, сжимающей газ . Сила, действующая на единицу площади поверхности поршня S со стороны газа, есть давление газа Р. Поэтому можно выразить величину силы через давление: . Тогда элементарная работа газа будет равна: . Но есть величина приращения объёма газа. Тогда элементарная работа газа равна:

, (4.7)

а работа внешней силы по сжатию газа равна .

Для определения работы по перемещению поршня на значительную величину , в результате которой объём газа изменяется на , нужно учесть процесс, происходящий с газом. Работу в этом случае определяют через интеграл:

(4.8)

Работа газа (или над газом) зависит от процесса (т.е. от последовательности промежуточных состояний) и поэтому является функцией процесса. Работа не является полным дифференциалом, отсюда и обозначение элементарной работы , а не dA.

Рассмотрим работу, совершаемую газом, при различных процессах. Будем обозначать в дальнейшем элементарную работу газа просто через и считать её положительной, если газ расширяется (), и отрицательной, если газ сжимают ().

Рассмотрим изохорический процесс. При изохорическом процессе объём газа не изменяется, приращение объёма равно нулю, следовательно, работа газа равна нулю.

Поскольку работу в любом случае можно определить, пользуясь формулой (4.8), для математической интерпретации работы удобно изображать любой процесс на диаграмме (P,V) . Работа на такой диаграмме равна площади фигуры под кривой, изображающей тот или иной процесс, происходящий с газом.

Рассмотрим изобарический процесс (рис. 4.2). Используя формулу (4.8) найдём работу газа при переходе из состояния 1 в состояние 2: .

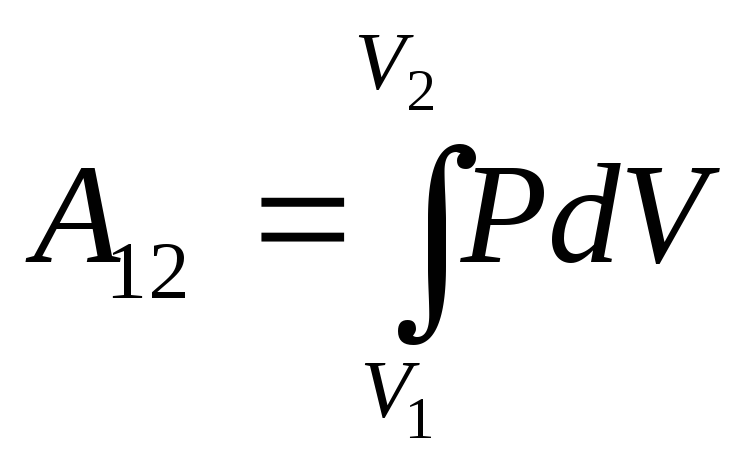Так как для данного количества вещества давление остаётся постоянным при изобарическом процессе, то его можно вынести за знак интеграла, тогда получим :

. Обозначим . С учётом этой записи работа при изобарическом процессе определяется по формуле:

(4.9)

Используя рис. 4.2, можно записать работу через указанные параметры состояния: . Такую же формулу мы получим, находя площадь заштрихованного прямоугольника. Часто бывает удобно выражать работу через изменение температуры. Для этого нужно использовать уравнение состояния идеального газа (уравнение Менделеева – Клапейрона) для 1 и 2 состояний: и . Вычитая из второго уравнения первое, получим:

(4.10)

При изобарическом сжатии конечный объём меньше начального и работа газа отрицательна, то есть газ препятствует сжатию.

Формула (4.7) позволяет выразить физический смысл молярной постоянной R . Для одного моля вещества () работа определяется как . Отсюда ясен физический смысл R , которая определяется работой изобарического расширения одного моля идеального газа при изменении температуры на один кельвин.

Рассмотрим изотермический процесс (рис.4.3). При изотермическом процессе температура остаётся постоянной, а давление и объём связаны между собой обратно пропорциональной зависимостью. В этом случае, используя формулу (4.8) для определения работы, уже нельзя вынести давление за знак интеграла. Давление выразим из уравнения Менделеева – Клапейрона: . Подставим правую часть этого уравнения в (4.8) и вынесен за знак интеграла все постоянные:

. Учитывая, что разность логарифмов есть логарифм отношения, получим:

(4.11)

Используя закон Бойля- Мариотта: , можем выразить работу и через отношение давлений:

(4.12)

Рассмотренные примеры подтверждают, что работа является функцией процесса. Следует отметить ещё один важный факт. С точки зрения математики функция процесса не является полным дифференциалом, а функция состояния – является полным дифференциалом. Поэтому для обозначения элементарной работы был использован знак а не d – знак полного дифференциала.