Лекции по молекулярной физике / Лекция 4

3.2 Статистические распределения

Изучение случайных явлений показывает, что многие случайные величины имеют плотность распределения вероятности, выраженную формулой:

(3.14)

где - среднее значение случайной величины Х, - среднее квадратичное отклонение.

Распределение, описываемое формулой (3.14) для множества значений случайной величины Х, называется распределением Гаусса или нормальным распределением в дифференциальной форме. Дифференциальное распределение Гаусса при различных среднеквадратичных отклонениях приведено на рис.3.4. Если максимум f(x) приходится на х=0, то распределение называется центрированным. Для распределения Гаусса характерно следующее: во-первых, симметрия относительно среднего значения случайной величины, во-вторых, вероятность нахождения случайной величины в интервале от до равна 0,68. Это означает, что площадь криволинейной трапеции в указанном интервале, составляет 68% от всей площади. Примерами распределения Гаусса являются: распределение частиц крупы по вертикальным ячейкам доски Гальтона, распределение молекул идеального газа по компонентам скоростей, распределение частиц по потенциальным энергиям в поле силы тяжести, распределение атмосферного давления по высоте при неизменной температуре.

Интегральное распределение Гаусса для центрированного распределения имеет вид, представленный на рис. 3.5.

В ряде случаев используют закон равномерного распределения вероятностей. Плотность вероятности в этом случае задаётся так: f(x)=0 при x<a ; f(x)=c при a<x<b; f(x)=0 при x>b.

Вид равномерного распределения приведён на рисунках 3.6 и 3.7.

Достаточно часто используется распределение Гаусса. В силу важности данного распределения в курсе молекулярной физики рассмотрим более подробно его применение на примере вывода барометрической формулы и распределения Больцмана.

3.3. Барометрическая формула. Распределение Больцмана

Барометрическая формула выражает закон изменения атмосферного давления при изменении высоты воздушного столба..

Известно, что атмосферное давление с высотой уменьшается. Установим закон изменения атмосферного давления в зависимости от высоты. Упростим задачу, считая температуру постоянной и не изменяющейся с высотой. При возрастании высоты на небольшую величину dx давление уменьшается на малую величину , где  - плотность газа,  = m₀n, m₀ - масса молекулы. Удобно выразить плотность газа через макропараметры – температуру и давление. Для этого воспользуемся формулой (2.5) и получим , тогда , а .

Разделим переменные

Интегрируя, получаем:

, где С - постоянная интегрирования, которую находим из условия : при x=0 и С=Р₀ . Тогда

или .

После потенцирования получим барометрическую формулу

. (3.15)

Учитывая, что масса молекулы может быть выражена через молярную массу и число Авогадро , а , показатель экспоненты можно записать через молярную массу и универсальную газовую постоянную:

(3.15')

Так как при постоянной температуре P  n , то можно получить выражение для распределения Больцмана или . Числитель показателя экспоненты представляет собой потенциальную энергию частицы, находящейся в поле силы тяжести, а знаменатель пропорционален тепловой энергии. Распределение Больцмана справедливо, если частица находится в любом потенциальном поле, поэтому можно обозначить потенциальную энергию частицы через U(х). Тогда распределение Больцмана будет иметь вид

(3.16)

Распределение Больцмана – это распределение частиц по потенциальным энергиям. Потенциальная энергия зависит от выбора начала отсчёта, и может быть выражена как U(x) = U₀ + U(x). Здесь U₀ – потенциальная энергия частиц в начале отсчёта, U(x)- потенциальная энергия в положении x, U(x)- изменение потенциальной энергии или рассматриваемый интервал потенциальных энергий. Число частиц, потенциальные энергии которых лежат в малом интервале U(x) от U₀ до U(x) , согласно (3.16), равно:

.

Число частиц, потенциальные энергии которых лежат в малом интервале U(x) вблизи U(x) , равно: .

Доля частиц, потенциальные энергии которых лежат в малом интервале U(x) вблизи U(x) , определяется выражением: . Отсюда видно, что доля частиц , потенциальная энергия которых лежит в заданном интервале U с ростом U уменьшается, а с ростом интервала U вблизи некоторого значения энергии U увеличивается.

При большом числе частиц n₀ и бесконечно малом интервале энергий dU доля частиц, потенциальная энергия которых лежит в в интервале dU вблизи потенциальной энергии U, имеет смысл вероятности того, что любая частица может иметь потенциальную энергию в указанном интервале вблизи заданного значения потенциальной энергии.

Сравнивая формулы (3.15) и (3.16) с формулой (3.14), можем заключить, что они весьма схожи.

Таким образом, барометрическая формула и распределение Больцмана по потенциальным энергиям имеет вид распределения Гаусса.

3.4. Броуновское движение. Опыт Перрена

Немаловажное значение имеет экспериментальное подтверждение полученных распределений. Большую роль в этом сыграло изучение броуновского движения.

Броуновское движение - движение частиц, взвешенных в жидкости или газе, под действием некомпенсированных ударов молекул жидкости или газа. Небольшие броуновские частицы можно трактовать как невзаимодействующие молекулы очень больших размеров. Поэтому можно ожидать, что броуновские частицы, взвешенные в жидкости и подверженные действию силы тяжести, будут распределены по высоте так же, как молекулы газа, то есть по закону (3.16). Этот факт использовал Перрен для опытной проверки барометрической формулы. 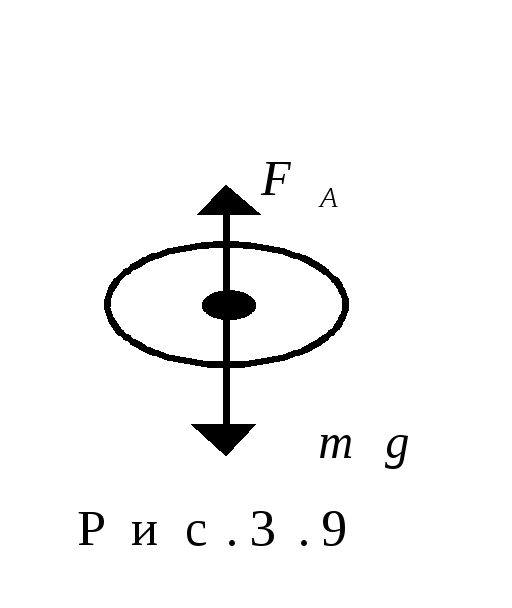Броуновские частицы можно наблюдать, используя микроскоп с большим увеличением. На броуновскую частицу действует сила тяжести и архимедова сила (рис.3.9). Величина архимедовой силы равна: .

Результирующая сила, действующая на броуновскую частицу, равна: и направлена вниз по ходу движения частицы.

Массу частицы и массу жидкости можно выразить через плотность и объём и , тогда

С учётом этого распределение броуновских частиц, взвешенных в жидкости, будет иметь вид:

или (3.17)

Подсчитав число броуновских частиц n₁ и n₂ на разных высотах х₁ и х₂, можно экспериментально подтвердить выполнение закона Больцмана. Проверка закона Больцмана таким способом требует подсчёта очень большого числа частиц на различных высотах и их усреднения на каждой высоте. На это требуется достаточно много времени, в течение которого необходимо выполнить условие Т=const . Поэтому экспериментаторы используют лампу дневного света для подсветки ванночки с взвешенными в воде броуновскими частицами, поскольку она выделяет меньше тепла в окружающее пространство, чем обычная лампа накаливания.