2.2. Виды графов.

Опр.3.12. Конечный граф - это граф G = (X, U), у которого количество его вершин |X| конечно. Конечный граф представлен на рис. 3.9.

Опр.3.13. Нуль-граф - это граф G = (X, U), состоящий только из изолированных вершин, т.е. граф, не содержащий ни одного ребра (|U| = 0). Такой граф обозначается G₀.

Нуль-граф, у которого |X| = 5 и |U| = 0 представлен на рис. 3.9.

Рис. 3.9. Нуль-граф с пятью вершинами.

Опр.3.14. Пустой граф - это граф G = (X, U), не содержащий ни вершин, ни рёбер (|X| =0, |U| = 0). Такой граф обозначается G_ø.

Опр.3.15. Неориентированный граф (неограф) - это граф G = (X, U), для каждого рёбра которого несуществен порядок двух его концевых вершин.

Неограф представлен на рис. 3.8. Рёбра неографа иногда называют звеньями.

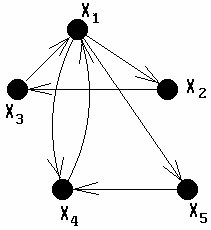
Опр.3.16. Ориентированный граф (орграф) - это граф, для каждого ребра которого существен порядок двух его концевых вершин.

Орграф представлен на рис. 3.10 и обозначается . Рёбра орграфа иногда называют дугами.

Рис. 3.10. Орграф.	Рис. 3.11. Смешанный граф.

Опр.3.17. Смешанный граф - это граф, который содержит как ориентированные, так и неориентированные рёбра. Смешанный граф обозначается .

Смешанный граф представлен на рис. 3.11.

Любой из перечисленных видов графа может содержать одно или несколько рёбер, у которых оба конца сходятся в одной вершине, т.е. u_ij є U, u_ij = (x_i, x_j), i = j. Такие рёбра называются петлями. На рис. 3.12 представлен смешанный граф с петлями.

Рис. 3.12. Смешанный граф с петлями.	Рис. 3.13. Мультиграф.

В общем случае множество рёбер U может состоять из трёх непересекающихся подмножеств: подмножества звеньев, подмножества дуг и подмножества петель.

Ребро u_ij, соединяющее вершины x_i и x_j, инцидентно данным вершинам и наоборот, вершины x_i и x_j инцидентны ребру u_ij. Ребро u₁₂ (рис. 3.13) инцидентно вершинам x₁ и x₂, а вершины x₁ и x₂, в свою очередь, инцидентны ребру u₁₂.

Опр.3.18. Мультиграф (рис. 3.13) - это граф, у которого любые две вершины соединены более чем одним ребром.

Опр.3.19. Рёбра, соединяющие одну и ту же пару вершин, называются кратными.

Опр.3.20. Наибольшее число кратных рёбер, соединяющих какую-либо пару вершин, называется мультичислом.

Мультичисло графа, представленного на рис. 3.13, m = 5.

Опр.3.21. Скелет мультиграфа - это граф, полученный из исходного мультиграфа путём удаления петель и сведения кратных рёбер в одно ребро.

На рис. 3.14 показан скелет мультиграфа, представленного на рис. 3.13.

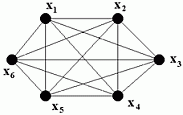
Опр.3.22. Полный граф (рис. 3.15.) - это граф, у которого любые две вершины соединены ребром. Полный граф обозначается G_п.

Рис. 3.14. Скелет мультиграфа.	Рис. 3.15. Полный граф.	Рис. 3.16. Плотный граф.

Опр.3.23. Плотный граф (рис. 3.16.) - это полный граф, у которого при каждой вершине имеется петля. Плотный граф обозначается G′_п.

Опр.3.24. Изоморфные графы - это два графа G = (X, U) и G′ = (X′, U′), у которых можно установить взаимно однозначное соответствие X ↔ X′, U ↔ U′, такое, что, если x_i, x_j є X соответствует x′_i, x′_j є X′ то ребро u_ij є U соответствует ребру ребро u′_ij є U′.

На рис. 3.17 и 3.18 показаны изоморфные графы G₁ и G₂, у которых вершинам x₁, x₂, x₃, x₄, x₅, x₆ поставлены во взаимно однозначное соответствие вершины x′₁, x′₂, x′₃, x′₄, x′₅, x′₆.

Рис. 3.17.	Рис. 3.18.

Опр.3.25. Плоский граф - это граф G = (X, U), у которого рёбра расположены на плоскости таким образом, что пересекаются только в вершинах.

Опр.3.26. Планарный граф - это граф G = (X, U), изоморфный плоскому графу.

Опр.3.27. Смежными вершинами называются любые две вершины x_i, x_j є X графа G = (X, U), инцидентные одному и тому же ребру.

Так, например, вершины x_i и x_j (рис. 3.1) являются смежными, а вершины x₄ и x₅ смежными не являются, так как не соединены между собой, т.е. ребро u₄₅ отсутствует.

Опр.3.28. Локальной степенью (или просто степенью) вершины x_i графа G = (X, U) называется количество рёбер ρ(x_i), инцидентных данной вершине.

Сумма локальных степеней всех вершин графа G = (X, U) есть удвоенное количество всех его рёбер:

Поскольку для полного графа ρ(x₁) = ρ(x₂) = ... = ρ(xn) = n - 1, то в этом случае

.

Опр.3.29. Граф называется однородным степени t, если локальные степени всех его вершин равны между собой, т.е. ρ(x₁) = ρ(x₂) = ... = ρ(x_n) = t.

Количество рёбер однородного графа степени t равно

.
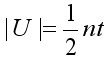