Методы построения плановых геодезических сетей.
Триангуляция – система примыкающих друг к другу треугольников в которых измерены все углы и, по меньшей мере одна сторона. По теореме синусов можно вычислить длины остальных сторон, а затем определить координаты всех пунктов.
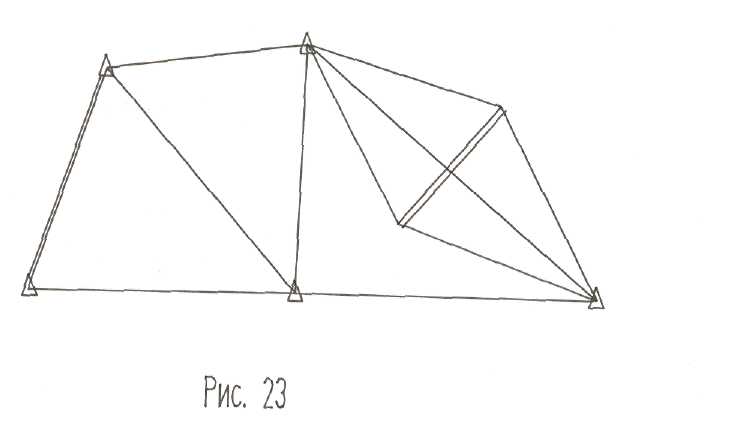
Трилатерация – система треугольников с измеренными всеми сторонами. Далее вычисляют углы по математическим формулам и координаты всех пунктов.
Полигонометрия – система ходов в виде ломаных линий, с измеренными сторонами и углами.
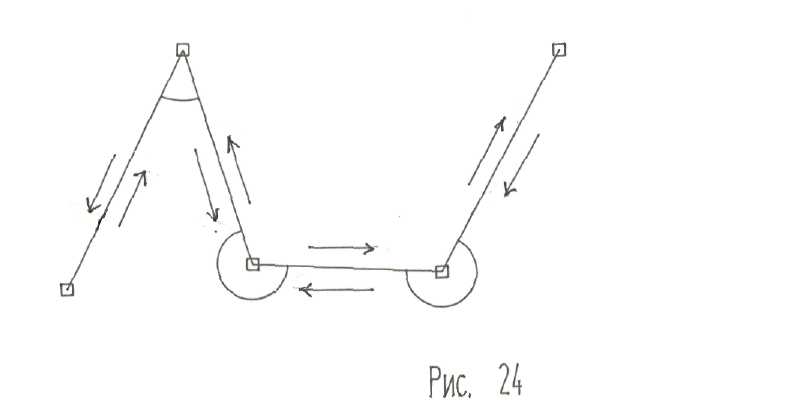
Теодолитные ходы – тоже система ломаных линий с измеренными углами и сторонами, но с меньшей точностью.
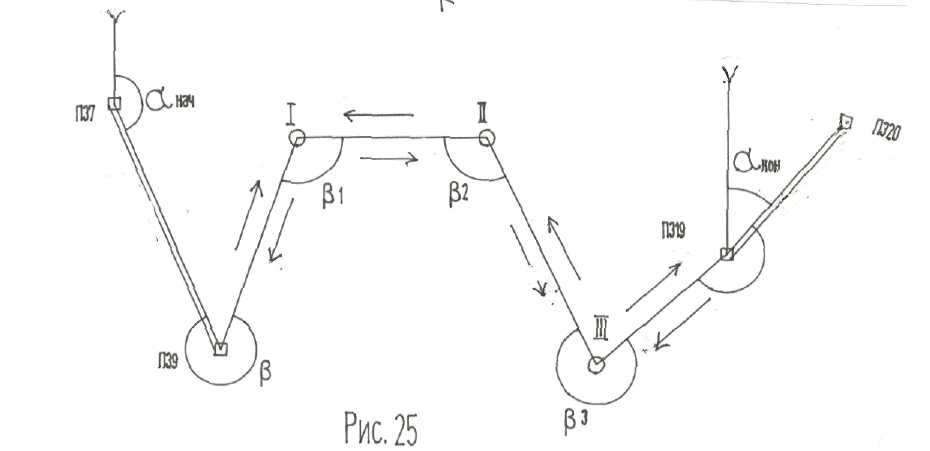
Вершины теодолитных ходов закрепляют на местности металлическими стержнями (трубками), кованными гвоздями, забиваемыми в асфальт, деревянными столбиками и т.п. Их в дальнейшем используют как опорные точки для съемки местности и рельефа, а также выноса проекта зданий или сооружений в натуру.
Углы в теодолитных ходах измеряют одним полным приемом (КЛ и КП). Стороны измеряют стальными рулетками, металлическими лентами или дальномерами в прямом и обратном направлениях.
Для вычисления координат вершин теодолитного хода надо иметь дирекционные углы его сторон. С этой целью выполняют «привязку» теодолитного хода к пунктам с известными координатами.
Вычислительная (математическая) обработка теодолитных ходов.
1. Обработку удобнее начать с составления схемы хода, на которую полезно выписать величины измеренных углов и горизонтальные проложения сторон, а также показать дирекционные углы начального и конечного направлений.
2. Для «увязки» (уравнивания) измеренных углов подсчитываем их сумму.
∑
=∑
=889º28.7/
Вследствие неизбежных погрешностей при измерении углов практически полученная сумма будет отличаться от теоретической.
∑
=αнач.+180ºxn-αкон.=299º34.2’+900º-310º07.5’
= 889º26.7’
Разность между практической и теоретической суммой углов называется угловой невязкой.
=+2.0’
Величина полученной невязки характеризует качество измерений углов которая не должна превышать допустимой величины.
допуст.=1’. √n=1√5=±2.2
Если угловая
невязка хода меньше или равна допустимой,
то выполняют уравнивание измеренных
углов, т.е. в измеренные углы вводят
поправки,
.
:n
Сумма поправок
д.б. равна невязке хода с обратным знаком.
Контроль:
∑ =
Вычисляем исправленные углы:
испр.=
измер.+
и подсчитываем их сумму:
∑
=
1+
+…+
Контроль уравнивания углов выполняем по формуле:
∑ =∑
Вычисляем дирекционные углы сторон хода:
αn+1=αn+180–
Например:
29º34,2 ’=
+180º
-209º34,2’
+3600
569º34,2’
-330º58,9’
238º 35,3’(8-1) =
+180º
418º35,3’
-50º58,2’
367º37,1’ =
-360º
7º37,1’(1–2) =
Вычисляем приращения координат (∆x и ∆y) решением прямой геодезической задачи.
Прямая геодезическая задача.
Цель: вычислить (передать) координаты с предыдущих точек на последующие, имея дирекционные углы и горизонтальные проложения.
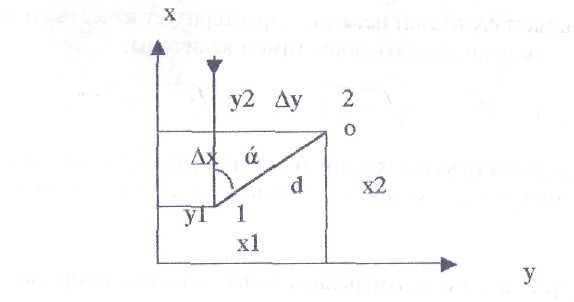
Дано: x1 и y1 α1-2, d1-2 |
Требуется определить: X и Y X2 и Y2 |
Приращения координат X и Y являются ортогональной проекцией линии 1 – 2 на соответствующие оси координат, и представляют собой катеты прямоугольного треугольника.
X=d*Cosα (или R)
Y=d*Sinα (или R)
Следовательно координаты последующей точки равны координатам предыдущей (данной) точки плюс соответствующие приращения координат.
Х2=Х1+ X
Y2=Yl+ Y
Для удобства пользования таблицей тригонометрических функций дирекционные углы α переводят в румбы и знаки ∆х и ∆у выбирают по названию румбов (Методичка к КР № 1).