Глава 2. Исследование устойчивости и качества сау

2.1. Устойчивость динамических систем

Всякая система автоматического управления и регулирования должна быть работоспособной, т.е. должна нормально функционировать и быть нечувствительной к посторонним возмущениям различного рода (помехам, шумам и т.п.). Работоспособность системы обусловлена одной из основных динамических характеристик САР ­­- ее устойчивостью. Для выполнения любых практических задач управления и регулирования система должна быть устойчивой, т.е. это требование является необходимым (но, как мы видим дальше, недостаточным) условием функционирования.

Устойчивость - это свойство системы возвращаться в исходный или близкий к нему установившийся режим после выхода из него в результате какого-либо воздействия. Если САР не может восстановить первоначальный режим, то такой переходный процесс называется расходящимся, а система – неустойчивой.

Неустойчивый переходный процесс может иметь характер колебаний с возрастающей амплитудой, как показано на рис. 2.1 б, или он может монотонно удаляться, как это показано на рис. 2.1а.

Если САР восстанавливает первоначальный режим, то такой переходный процесс называется сходящимся, а система – устойчивой. Виды устойчивых переходных процессов показаны на рис. 2.2, а и б.

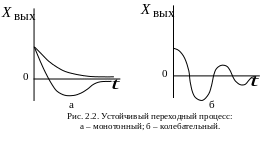
Есть особый случай, когда система переходит в новое установившееся состояние, которое может иметь незатухающие колебания постоянной амплитуды (автоколебания) или монотонно перейти на другой постоянный уровень. Эти примеры иллюстрируются на рис. 2.3. Такие системы называются нейтральными. Для суждений об их устойчивости нужны дополнительные исследования. В теории автоматического управления разработаны математические методы исследования устойчивости. Основой такого исследования являются дифференциальные уравнения, описывающие поведение САР.

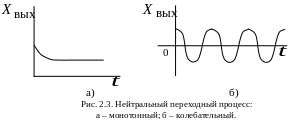
Путем нахождения переходного процесса (решения уравнений относительно регулируемого параметра ) можно судить по его виду об устойчивости (или неустойчивости) системы. Это так называемый прямой метод исследования устойчивости, который обладает двумя существенными трудностями, а именно: во-первых, реальные САР являются нелинейными или имеют распределенные параметры, что значительно усложняет получение точного аналитического решения; во-вторых, для линейных или линеаризованных систем, описываемых уравнениями выше четвертого порядка, получить решение в общем виде невозможно. Естественно, что за время своего развития теория управления накопила методы разрешения этих трудностей.

Первые разрешаются линеаризацией нелинейных САР для случаев, когда это математически корректно. Исследование реальной системы заменяется исследованием ее линейного приближения. При этом возникает проблема адекватности линейного приближения и реальной САР, т.е. можно ли судить об устойчивости реальной системы по устойчивости ее линейного приближения. Ответ на этот вопрос дает теория устойчивости движения динамических систем, созданная русским ученым А.М.Ляпуновым. Три теоремы, сформулированные и доказанные им, позволяют судить об устойчивости систем по первому приближению, в области малых отклонений регулируемого параметра, т.е. по линеаризованным уравнениям. Практически это означает, что для решения задачи устойчивости, достаточно исследовать переходный процесс при бесконечно малом отклонении системы от базового положения равновесия.

Теорема 1. Если вещественные части всех корней характе-ристического уравнения системы первого приближения (линеаризованной системы в области отклонений регулируемого параметра) отрицательны, то нулевое решение исходной системы асимптотически устойчиво независимо от членов разложения выше первого порядка.

Теорема 2. Если среди корней характеристического уравнения системы первого приближения имеется хотя бы один с положительной вещественной частью, то нулевое решение исходной системы дифференциальных уравнений неустойчиво независимо от членов разложения выше первого порядка.

Теорема 3. Если среди корней характеристического уравнения первого приближения есть нулевые, то в этом случае для суждения об устойчивости нулевого решения исходной системы необходимо учитывать члены выше первого порядка.

Для преодоления вторых трудностей, вызванных высоким порядком исходных уравнений, в теории управления разработаны признаки, которые без решения характеристического уравнения позволяют судить об устойчивости конкретной САР. Такие признаки носят название критериев устойчивости.

В соответствии с данным выше определением устойчивости, об устойчивости системы можно судить по сходимости переходного процесса после прекращения внешних воздействий. В математическом плане это значит, что об устойчивости САР можно судить по виду ее свободного движения, которое описывается однородным дифференциальным уравнением с постоянными коэффициентами:

(2.1)

Решение уравнения (2.1) в общем виде имеет вид:

(2.2)

где С₁, С₂, …, С_n - постоянные интегрирования, определяемые из начальных условий;

S₁, S₂, …, S_n - корни характеристического уравнения:

(2.3)

Переходный процесс x(t) в теоретическом плане представляет собой сумму составляющих . В нашем случае x(t) – это регулируемый параметр . Характер свободного движения САР определяется видом корней S₁, S₂, …, S_n , которые могут быть вещественными, комплексными попарно сопряженными, мнимыми попарно сопряженными, нулевыми и кратными. Рассмотрим эти случаи подробнее.

1. Все корни уравнения (2.3) вещественные и неравные. В этом случае свободное движение системы описывается суммой экспонент (2.2). Если все корни отрицательные, то каждая из экспонент будет с течением времени стремиться к нулю, и переходный процесс будет затухающим, как это показано на рис. 2.2 а. Если среди корней будет хотя бы один положи-тельный корень S_к >0, то составляющая 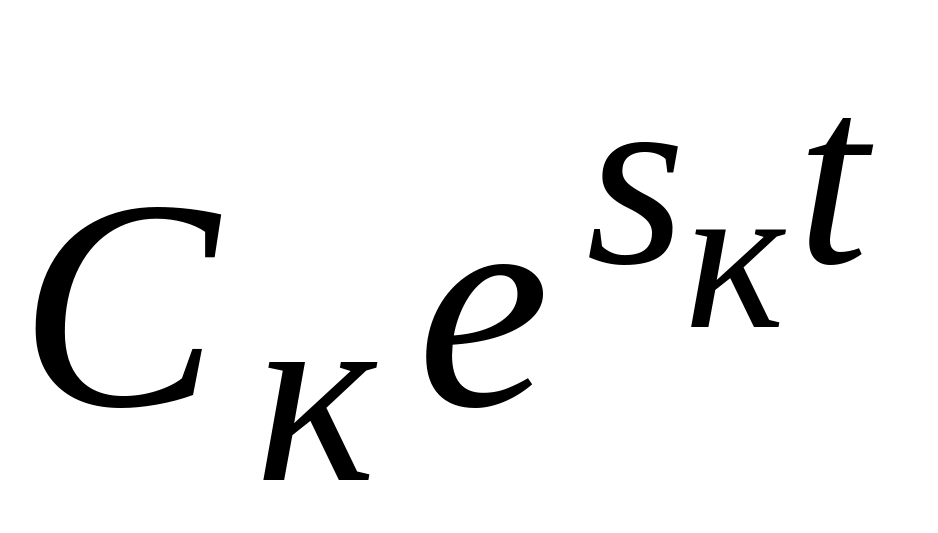с течением времени будет неограниченно расти и весь процесс будет незатухающим, как это показано на рис. 2.1 а.

2. Характеристическое уравнение имеет пару комплексных сопряженных корней 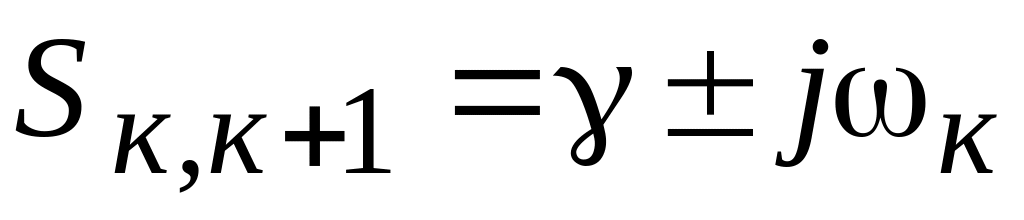. Остальные корни вещественные и отрицательные. Комплексным корням в правой части уравнения (2.2) будут соответствовать слагаемые

(2.4)

где А_к - амплитуда, _к - фаза.

Амплитуда колебаний не остается постоянной, а изменяется во времени из-за множителя . Если вещественная часть _к комплексного корня отрицательна, то процесс будет затухать (см. рис. 2.2 б), если же _к положительна, процесс будет незатухающим (см. рис. 2.1 б).

3. Характеристическое уравнение имеет пару мнимых сопряженных корней 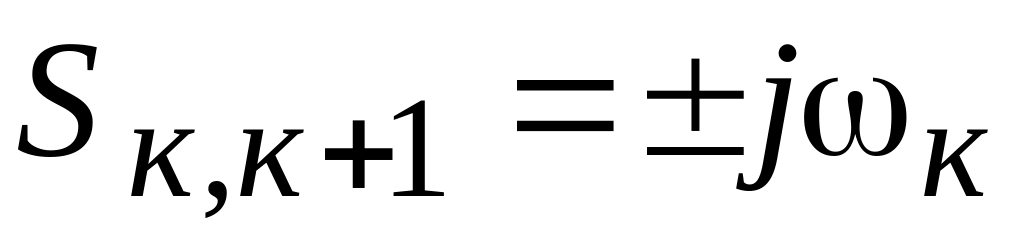. Остальные корни вещественные и отрицательные. В этом случае в решении уравнения (2.2) паре мнимых корней будет соответствовать составляющая вида (2.4), у которой показатель степени равен нулю (_к=0), и переходный процесс для нее будет иметь вид незатухающих колебаний (рис. 2.3б) с постоянной амплитудой.

4. Характеристическое уравнение имеет нулевой корень S_к=0. Составляющая переходного процесса (2.2), соответствующая нулевому корню, является постоянной: 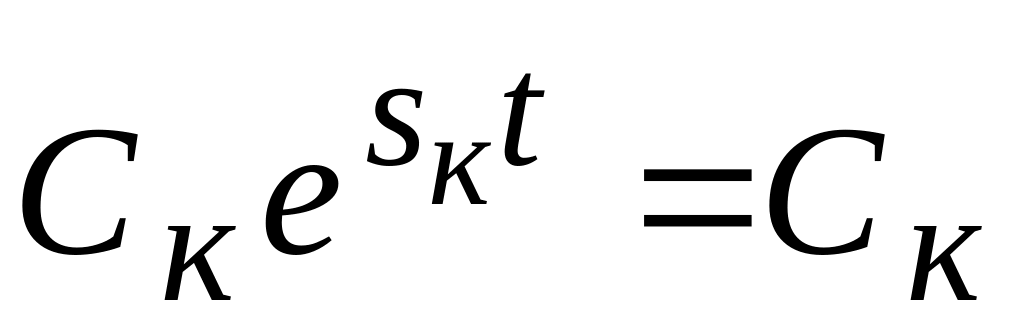. Если все остальные корни имеют отрицательные вещественные части, то с течением времени переходный процесс будет стремиться к постоянной величине (рис. 2.3 а).

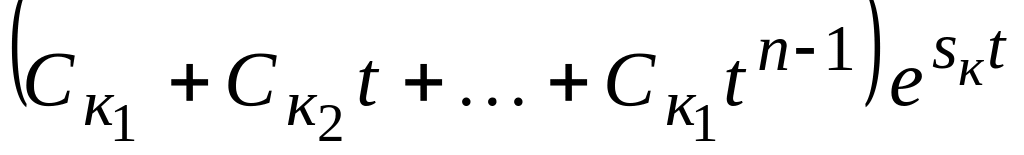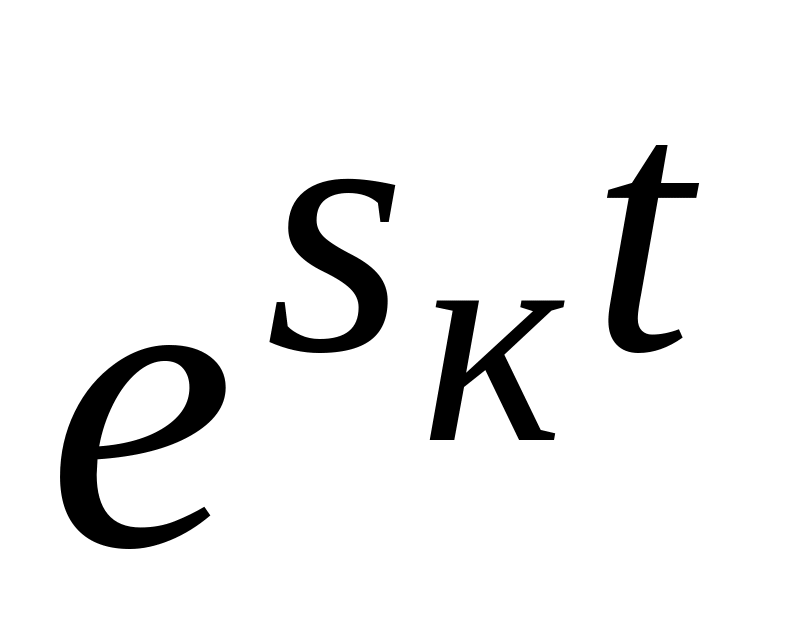5. Характеристическое уравнение имеет n кратных вещественных корней S_к. Тогда в выражении переходного процесса (2.2) появится составляющая . Многочлен в скобках неограниченно возрастает при t  . Множитель при отрицательном S_к стремится к нулю быстрее, чем многочлен к бесконечности. Поэтому их произведение всегда стремится к нулю при S_к  0. Значит, для устойчивости системы достаточно, чтобы кратный вещественный корень S_к был отрицательным. Анализируя рассмотренные случаи, можно вывести одно общее правило: для устойчивости САР необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательные вещественные части.

При наличии хотя бы одного корня с положительной вещественной частью система будет неустойчивой. Если все корни имеют отрицательные вещественные части и при этом есть один нулевой корень или пара чисто мнимых сопряженных корней, то САР будет находиться на границе устойчивости и будет нейтральной. Нетрудно убедиться, что рассмотренные случаи соответствуют формулировкам теорем А.М.Ляпунова.

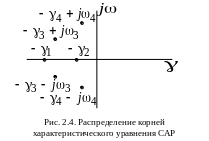
На рис. 2.4 показана примерная картина распределения корней характеристического уравнения устойчивой САР шестого порядка: две пары комплексных сопряженных корней и два вещественных корня. Отрицательность вещественной части означает, что корень лежит слева от мнимой оси. Значит, для устойчивости САР необходимо и достаточно, чтобы все корни ее характеристического уравнения лежали на плоскости корней слева от мнимой оси. Если хотя бы один корень окажется справа от мнимой оси, то система будет неустойчивой. Мнимая ось на плоскости корней соответствует границе устойчивости, на ней располагаются чисто мнимые и нулевые корни характеристического уравнения системы. Важная заслуга А.М.Ляпунова заключается в том, что ему удалось найти подход к определению свойства устойчивости, который базируется на очень простой идее, известной из механики, а именно: в положении равновесия любая динамическая система имеет минимум потенциальной энергии.

Известно, что минимум потенциальной энергии всегда можно считать равным нулю. Тогда в любой окрестности положения равновесия потенциальная энергия будет положительной. Применение функций, которые положительны всюду, за исключением положения равновесия, к анализу устойчивости и лежит в основе метода, разработанного А.М.Ляпуновым. Они названы функциями Ляпунова. Единого способа формирования функции Ляпунова для анализа конкретных САР не существует.