
Ильинский Н.Ф. Общий курс электропривода [pdf]
.pdf
Рис. 5.19. Схема пуска электропривода постоянного тока с двигателем независимого возбуждения
Если сравнить (**) с (3.4), то окажется, что уравнения идентичны, однако в (**) U′ за-
висит от dtdi , т.е. уравнение (**) представляет семейство прямых (рис. 5.20,а), параллельных
естественной характеристике и располагающихся как ниже ( dtdi > 0), так и выше ( dtdi < 0) нее.
При dtdi = 0, очевидно, уравнение (**) соответствует естественной характеристике.
После замыкания ключа К ток i начинает расти, значит растет М и привод разгоняется (для упрощения рассуждений примем Мс = 0), переходя при этом с характеристики на на ха-
рактеристику ( dtdi > 0, но уменьшается по мере разгона). В процессе увеличения тока и ско-
рости (участок Оа на рис. 5.20) возрастает запас энергии как в индуктивности, так и во вращающемся якоре. В точке а рост тока прекращается; при этом в соответствии с (*) привод оказывается на естественной характеристике, но М > Мс = 0. С точки а начинается спадание тока, т.е. энергия, запасенная в Lя, передается вращающемуся якорю. Механизм передачи очевиден из (*): напряжение, приложенное к якорю U′, становится больше, чем напряжение сети U. На участке аb привод разгоняется, соответственно растет е = сω, причем в точке b i = 0 – запас энергии в Lя исчерпан, однако ω >ω0 и e > U, т.е. в якоре запасена избыточная механическая энергия.
На участке bc под действием e > U ток изменяет направление, привод тормозится, при этом избыточная механическая энергия вновь переходит в электромагнитную энергию, нака-
пливаемую в индуктивности. В точке с dtdi = 0, однако в Lя запасена энергия, чему соответст-
вует i ≠ 0 и M ≠ 0. Привод продолжает тормозиться до точки d, затем процесс повторяется.
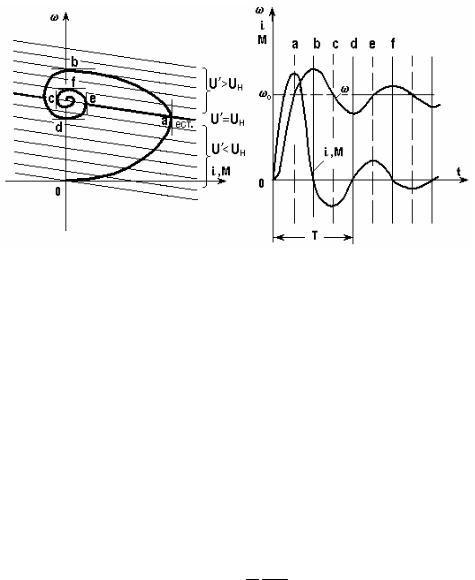
Кривая 0abcd... ω0 в плоскости ω – M представляет собою динамическую механическую характеристику. Соответствующие зависимости ω(t), i(t) или M(t) показаны на рис. 5.20,б.
а) б)
Рис. 5.20. Механические характеристики (а) и переходной процесс пуска при Lя ≠ 0 (б) Так как в якорной цепи есть сопротивление Rя процесс перекачивания энергии сопро-
вождается ее рассеиванием, вследствие чего система после ряда колебаний приходит в точку
ω0, соответствующую установившемуся режиму. Если бы сопротивление Rя было равным нулю, колебания ω и М имели бы незатухающий характер. Если, наоборот, Rя велико, энергии, запасенной в Lя на участке 0а, может оказаться недостаточно для покрытия потерь в Rя и
вывода якоря в точку ω > ω0 при i = 0. В этом случае процесс будет иметь апериодический характер.
Количественное описание рассмотренных выше процессов можно получить, решив совместно (5.1) и (5.23). Из (5.1) при Мс = 0 следует:
i = Jc ddtω .
Подставив это выражение и его производную
di |
= |
J d 2 |
ω |
|||
|
|
|
|
|
||
dt |
c dt |
2 |
||||
|
||||||
в (5.23), получим после элементарных преобразований:
|
ω +Т м |
dω |
+T мТя |
d 2ω |
= ω0 |
, |
(5.24) |
||||||
|
dt |
|
dt 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
||
Т м = |
JR я |
; Тя |
= |
L я |
; ω0 = |
U н |
. |
|
|
||||
|
|
|
|||||||||||
|
|
|
|
|
|||||||||
|
с2 |
|
|
|
Rя |
|
|
с |
|
|
|||
Решение (5.24) найдем в виде |
|
|
|
|
|
|
|
|
|
|
|
||
ω = ωсв + ωпр = А1 ер1t + A2 e p2t + ω0, |
|
(5.25) |
|||||||||||
где А1, А2 – постоянные, определяемые по начальным условиям |
|
|
|||||||||||
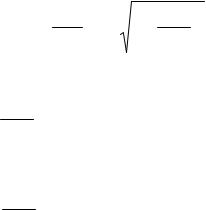
|
ω t=0 и |
|
dω |
|
|
t =0 ; |
|
|
|
||||||
|
|
dt |
|
||||
|
|
|
|
|
|
||
p1, p2 – корни характеристического уравнения |
|
|
|
||||
1 + Тмр + ТмТяр2 = 0 |
(∆) |
||||||
Решив (∆), получим |
|
|
|
|
|
|
|
p |
= − 1 |
( 1 ± |
1 − 4Тя ) , |
||||
1,2 |
2Tя |
|
|
Т м |
|||
|
|
|
|||||
откуда вытекает условие колебательности процесса. Если
4Тя > 1, т.е. Тм < 4Тя,
Т м
корни комплексные и процесс носит колебательный характер; если
4Тя ≤ 1, т.е. Тм ≥ 4Тя,
Т м
корни действительные и процесс апериодический.
Уравнение для тока или момента легко получить, воспользовавшись, как и прежде, (5.15). Продифференцировав (5.25) и умножив результат на J получим:
М = J ( А1 ер1t + A2 e p2t ). |
(5.26) |
б) Переходные процессы в системе ИТ-Д, замкнутой по скорости
Рассмотрим переходные процессы в системе ИТ-Д (п. 3.7) на участке, где действует отрицательная обратная связь по скорости. Если при анализе установившихся режимов мы не учитывали индуктивность цепи возбуждения, то теперь это сделать необходимо, так как момент в этой системе определяется iв, а изменение этого тока связано с Lв.
Уравнения динамики для схемы на рис. 5.21 имеют вид (примем, как и в предыдущем случае, что Мс = 0):
М = J |
dω |
; |
|
(5.27) |
|
|
|||||
|
dt |
|
|
|
|
U в = iвR в + L в |
diв |
, |
(5.28) |
||
|
|||||
|
|
|
dt |
|
|
где Uв – напряжение на обмотке возбуждения;
Rв, Lв – активное сопротивление и индуктивность цепи возбуждения; iв – текущее значение тока возбуждения.

Рис. 5.21. Схема системы источник тока – двигатель, замкнутой по скорости Эти уравнения отражают динамические свойства системы, так как содержат члены
члены с J и Lв. Кроме того, следует записать уравнения, отражающие связи между переменными.
Из общего уравнения для момента (3.1), приняв, что Ф = αiв, имеем:
М = kФI = kIαiв
или с учетом (5.27)
|
|
|
|
|
|
|
i |
= |
|
|
|
J |
|
|
dω |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
в |
|
|
|
|
kIα dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
di |
в |
|
= |
|
|
J |
|
|
|
|
d 2ω |
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
dt |
|
|
kIα dt 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Из уравнения замыкания системы при линейном безынерционном возбудителе получа- |
|||||||||||||||||||||||||||||||||||
ем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U в |
= KU вх |
= |
|
|
KU з |
|
|
− |
Kγω |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
R в |
|
|
R в |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
или с учетом (5.28) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
KU з |
|
− |
Kγω |
|
= iв |
+ |
|
L в |
|
|
|
|
diв |
|
. |
|
|
|
|
||||||||||||
|
|
|
|
Rв |
|
R |
в |
|
|
R в |
|
|
|
|
dt |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
После простых преобразований получаем окончательно: |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
ω +Т м |
|
dω |
|
+T мТв |
d 2ω |
|
= ω0 |
, |
(5.29) |
||||||||||||||||||||||
|
|
|
|
|
dt |
|
|
dt 2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где Т м = |
JRв |
|
– электромеханическая постоянная времени; |
|
|
||||||||||||||||||||||||||||||
kIαKγ |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тв = L в - постоянная времени цепи возбуждения;
Rв
ω0 = Uγз - скорость идеального холостого хода.
Сравнив (5.29) с (5.24), обнаруживаем полное сходство уравнений, хотя входящие в

них параметры совершенно различны. В этом факте проявляется глубокая физическая общность систем на рис. 5.19 и 5.21: каждая из них имеет по два накопителя энергии и существуют условия для обмена энергией между ними.
Очевидно, что уравнению (5.29) соответствуют процессы, рассмотренные в п.а).
в) Переходные процессы при изменении магнитного потока двигателя независимого возбуждения.
Рис. 5.22. Схема электропривода постоянного тока с двигателем независимого возбуждения при ослаблении поля
Рассмотрим еще один практически важный случай – изменение Ф в двигателе постоянного тока независимого возбуждения (рис. 5.22). В исходном состоянии ключ К замкнут и привод работает на естественной характеристике (рис. 5.22) в точке ωнач = ωс нач. Переходный процесс вызывается размыканием в момент t = 0 ключа К, в результате чего уменьшается ток iв и магнитный поток Ф и привод переходит на верхнюю характеристику. Если бы обмотка возбуждения не обладала индуктивностью, то ток iв изменился бы мгновенно, т.е. мгновенно исходная (естественная) характеристика заменилась бы конечной, и переходный процесс протекал по ней, как было описано в п.5.2 (пунктирные стрелки на рис. 5.23). В действитель-
ности же L ≠ 0, и переход от естественной характеристики к конечной происходит во времени, причем темп этого перехода в общем случае соизмерим с темпом изменения скорости. В результате динамическая механическая характеристика имеет вид, показанный на рис. 5.23 сплошной линией со стрелкой.
Рис. 5.23. Механические характеристики при ослаблении поля

Получим уравнение, описывающее изменение скорости. Для этого за основу, как и раньше, возьмем уравнение движения (5.1)
M − M c = J |
dω |
. |
|
|
|
|
(5.1) |
||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
Зависимость момента от скорости можно в соответствии с рис. 5.23 записать как |
|||||||||||||||||
М = М кз.i |
− |
М кз.i |
|
ω. |
(*) |
||||||||||||
ω |
0i |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставив (*) в (5.1), после простых преобразований получим |
|
||||||||||||||||
ω + |
|
Jω0i |
|
dω |
|
= ω0i − |
|
ω0i |
M c , |
|
|||||||
|
M кзi |
dt |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
M кзi |
|
||||||
или, если учесть, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0i |
= |
U |
|
и М кзi = k |
|
U |
Ф |
|
|||||||||
kФ |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R я |
|
|||
ω +Т м( Ф) |
|
dω |
= ωc( Ф) . |
(5.30) |
|||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
||
Вэтом уравнении, похожем внешне на (5.6), есть существенное отличие: Тм и ωс зависят от потока и растут с его уменьшением.
Всвою очередь, магнитный поток экспоненциально изменяется во времени, если принять зависимость Ф(iв) линейной.
Численное решение (5.30), подстановка ddtω в (5.1) и вычисление тока якоря по соот-
ношению
i = U − kΦω R я
приводят к результату, представленному на рис. 5.24 и имеющему, как и при всяком численном решении, частный характер.
Рис. 5.24. Переходный процесс при ослаблении поля
В данном случае переходной процесс определяется двумя инерционностями – J и Lв и описывался двумя дифференциальными уравнениями первого порядка, одно из которых бы-
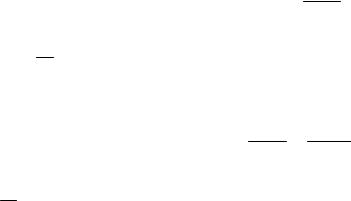
ло нелинейным. Эти уравнения не имели комплексных корней, в чем отразилась физическая невозможность обмена энергией между двумя накопителями.
5.5. Переходные процессы в системах
Рассмотренные ранее случаи переходных процессов относятся к простейшим электроприводам, когда учитываются лишь основные накопители энергии и можно уделять внимание физической стороне дела, относительно просто приходя к результату. Вместе с тем, все современные электроприводы представляют собой весьма сложные многоэлементные замкнутые системы, и для их анализа и синтеза приходится прибегать к приемам, разработанным в теории автоматического управления. Один из самых распространеных на практике приемов
– использование структурных схем с передаточными функциями входящих в систему эле-
ментов.
Передаточная функция – отношение изображений по Лапласу выходной величины к входной при нулевых начальных условиях. Так, для цепи R – L, подключенной к источнику напряжения u(t) имеем:
u( t) = i( t)R + L di( t) dt
или, заменив dtd на р, u(t) на u(p) и i(t) на i(p) и решив уравнение относительно i(p), приня-
том за выходную величину, получим
W ( p) = u( p) = T1/р+R1,
где T = RL – постоянная времени.
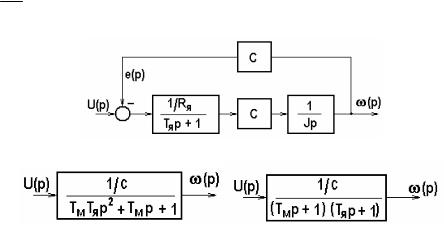
Для двигателя постоянного тока независимого возбуждения с учетом индуктивности якорной цепи Lя при питании якоря от источника напряжения u(t) и kФ = с, приняв за выход-
ную величину ω(t) и за входную u(t) после перехода к изображениям, получим для случая Мс = 0 структурную схему на рис. 5.25,а.
Проделав элементарные преобразования, будем иметь передаточную функцию двигателя в виде колебательного звена (рис. 5.25,б):
|
|
|
|
W ( p) = |
ω( p) |
= |
|
1 / c |
|
, |
|
|
|
|
u( p) |
T мT я р2 +Т м р+1 |
|||||
|
|
|
|
|
|
|
||||
где Т |
|
= |
JR я |
– электромеханическая постоянная времени, |
|
|||||
м |
с2 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
Т я = Lя – постоянная времени цепи якоря.
R я
а)
б) в)
Рис.5.25. Передаточные функции двигателя постоянного тока независимого возбуждения
Если корни характеристического уравнения действительные, будем иметь два апериодических звена (рис. 5.25, в):
W ( p) = |
ω( p) |
= |
|
1 / c |
|
|
. |
u( p) |
Т |
р+1 Т |
р+1 |
||||
|
|
|
( м |
)( |
я |
) |
|
Используя подобные действия, можно получить структурную схему любой системы и применить к ней приемы преобразования. анализа и синтеза, разработанные в теории автоматического регулирования.
Рассмотрим здесь кратко лишь один из таких приемов рационального управления динамической системой – построение систем подчиненного регулирования с последовательной коррекцией.
Для выходной координаты некоторого объекта регулирования образуют замкнутый контур, в который входит как сам объект, так и специальный регулятор, обеспечивающий заданное качество регулирования.
Пусть передаточная функция объекта регулирования имеет вид, к которому часто удается привести после преобразований передаточную функцию реального устройства:
W 0( p) = |
К |
|
|
|
1 |
|
, |
(5.31) |
|
Т р+1 |
k |
j |
) |
||||||
|
|
|
|
||||||
|
|
|
|
∏( |
|
|
|||
|
|
|
|
T |
|
p +1 |
|
|
|
j=1
где К – общий коэффициент передачи, Т – наибольшая постоянная времени, Тj – малые постоянные времени.
Поставим задачу максимально сократить время переходного процесса, исключив колебательность.
Рассмотрим сначала первый сомножитель в (5.31).

Теоретически возможно увеличить коэффициент передачи, включив на вход регулятор с передаточной функцией Wp(р)= K1, однако это повысит чувствительность к помехам и склонность к колебательности. Теоретически возможен регулятор с передаточной функцией Wp(р)= Tр+1, однако такой регулятор нереализуем физически. На практике обычно используют пропорционально-интегральный регулятор (ПИ-регулятор) с передаточной функцией
W p( p) = |
T р+1 |
= |
T |
+ |
1 |
. |
(5.32) |
|
KT0 p |
|
|
KT0 p |
|||||
|
|
KT0 |
|
|
||||
Тогда в разомкнутой структуре с таким регулятором будем иметь без второго сомножителя в
(5.31):
W |
раз |
( р) =W |
p |
( p)W ( p) = |
K(T р+1) |
= |
1 |
. |
|
|
|
||||||||
|
|
0 |
(T p +1)KT0 p T0 p |
||||||
|
|
|
|
|
|||||
Для выбора Т0 пользуются вторым сомножителем в (5.31). Если принять
k
T0 ≥ 2∑T j = 2Tµ ,
j=1
то, как показано в теории, можно считать, что
(5.33)
(5.34)
|
|
k |
|
|
|
|
|
|
|
|
|
|
∏(T j p +1) |
≈T µ p +1. |
|
|
(5.35) |
||||
|
|
j=1 |
|
|
|
|
|
|
||
Тогда, очевидно, передаточная функция разомкнутой системы будет |
|
|||||||||
W раз( р) = |
|
|
1 |
|
= |
1 |
|
, |
(5.36) |
|
Т 0 |
р(Т µ р+1) |
аТ µ р(Т |
µ р+1) |
|||||||
|
|
|
|
|||||||
а передаточная функция замкнутой системы определится как
W зам( р) = |
1 |
|
|
, |
(5.37) |
|
аТ µ р(Т µ |
р+1) +1 |
|||||
|
|
|
||||
где а = ТТµ0 – параметр, характеризующий вид переходного процесса; на рис. 5.26 приведе-
ны переходные функции для различных а. Очевидно, что компромисс между колебательностью и длительностью переходного процесса достигается при а = 2, и такая настройка (выбор Т0) называется настройкой на технический оптимум. При этом без большой погрешности можно принять, что
W зам( р) ≈ |
1 |
|
. |
(5.38) |
|
2Т µ р+1 |
|||||
|
|
|
|||
Итак, оптимизация объекта с передаточной функцией W0(р) имеет компромиссный характер, осуществляется включением ПИ-регулятора Wр(р) с замыканием системы по выходной координате и состоит в замене разомкнутой структуры с большой постоянной времени Т
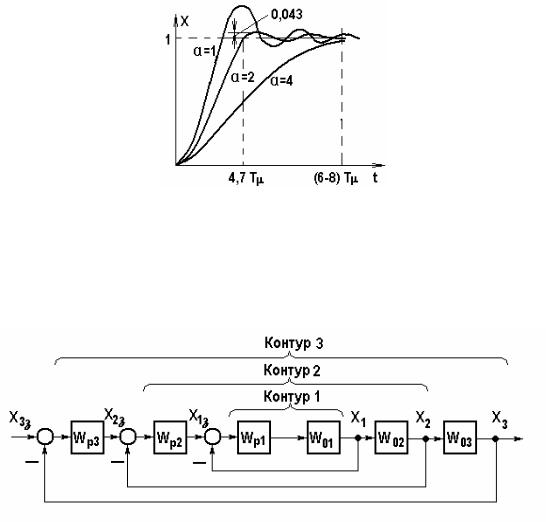
замкнутой структурой с аналогичной передаточной функцией, но с другой постоянной времени, выбираемой из условия желаемого качества переходных процессов.
Рис. 5.26. Характер переходных процессов в контуре при различных а = Т0/Тµ Изложенная процедура оптимизации особенно удобна и эффективна, если в систему
входит несколько контуров – рис. 5.27. Начав с внутреннего (контур 1) и оптимизировав его, как было описано выше, переходят к следующему контуру (контур 2) и действуют аналогичным образом.
Рис. 5.27. Многоконтурная система
Если принять для упрощения, что малые постоянные Тj, образовавшие некомпенсируе-
мую постоянную Тµ, сосредоточены во внутреннем контуре, а во внешнем отсутствуют, можно получить следующие передаточные функции i-ого контура:
|
W i раз( р) = |
|
1 |
|
|
|
|
|
|
(5.39) |
|
|
2iTµ p[ 2( i−1) Tµ p |
+1] |
|
|
|
||||||
|
|
|
|
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
W iзам( p) = |
|
|
1 |
|
≈ |
|
1 |
|
|
. |
(5.40) |
|
|
|
|
|
|
|
|
||||
|
|
2iTµ p[ 2( i−1) Tµ p +1] +1 2iTµ p +1 |
|
|
|||||||
К достоинствам изложенной оптимизации относится идентичность переходных процессов в каждом контуре при их независимой настройке, простота ограничения координат за счет ограничения задания нелинейной характеристикой вход-выход соответствующего регулятора, удобство в практической наладке систем. К недостаткам можно отнести сравнительно низкое быстродействие внешних контуров – см. (5.40).
