6.4 Анализ динамических рядов

6.4.1 Выявление тенденции изменения явления во времени

В ряде случаев тенденция развития явления отчетливо отражается уровнями динамического ряда (уровни ряда в течение рассматриваемого периода непрерывно растут или непрерывно снижаются). Однако часто приходится встречаться с такими рядами динамики, в которых уровни претерпевают самые различные изменения (то возрастают, то убывают), и общая тенденция развития неясна.

На развитие явления оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них действуют постоянно и формируют в рядах динамики определенную тенденцию. Воздействие других факторов является кратковременным или носит случайный характер.

Поэтому при анализе динамики явления речь идет о выявлении основной тенденции, устойчивой на протяжении изучаемого периода развития.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровней ряда динамики, свободное от случайных колебаний.

С целью выявления общей тенденции развития явления во времени ряды динамики подвергаются обработке с помощью следующих методов:

а) укрупнения интервалов;

б) скользящий средней;

в) аналитического выравнивания.

Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска, последний – рядом квартального выпуска и т.д. Средняя, исчисленная по укрупненным интервалам, позволяет судить о направлении и характере (ускорении или замедлении роста) основной тенденции развития.

Рассмотрим применение метода укрупнения интервалов на примере.

Таблица 6.4.1 Объем производства продукции предприятия (по месяцам) в плановых ценах, млн.руб.

месяц	Объем производства	месяц	Объем производства
Январь	5,1	Июль	5,6
Февраль	5,4	Август	5,9
Март	5,2	Сентябрь	6,1
Апрель	5,3	Октябрь	6,0
Май	5,6	Ноябрь	5,9
июнь	5,8	Декабрь	6,2

Колебания уровней производства по месяцам затрудняет выводы об основной тенденции производства. Но если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск за каждый квартал, то решение задачи упрощается.

Таблица 6.4.2 Объем производства продукции предприятия (по кварталам) в плановых ценах, млн.руб.

Квартал	За квартал	В среднем за месяц
I	15,7	5,23
II	16,7	5,57
III	17,6	5,87
IV	18,1	6,03

После укрупнения интервалов основная тенденция развития производства стала очевидной:

5,23<5,57<5,87<6,03 млн. руб.

Сущность метода скользящий средней заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3,5,7 и т.д.) первых по счету уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя как бы скользит по ряду динамики.

Расчет скользящей средней произведен по данным об урожайности (таблица 6.4.3).

Как видим, сглаженный ряд урожайности по трехлетним данным короче фактического ряда на один уровень в начале и в конце, по пятилетним данным – на два уровня в начале и в конце. Сглаженные ряды менее подвержены колебаниям из-за случайных факторов, что отражено на графике (рис. 6.4.1).

Таблица 6.4.3 Расчет скользящий средней урожайности зерновых культур

Годы	Урожайность зерновых культур, ц/га	Скользящая средняя
		трехлетняя	пятилетняя
1986	15,4	-	-
1987	14,0		-
1988	17,6		14,7
1989	15,4		15,1
1990	10,9		15,2
1991	17,5	14,5	17,1
1992	15,0	17,0	16,8
1993	18,5	15,9	17,6
1994	14,2	15,9	-
1995	14,9	-	-

Рис. 6.4.1 Динамика урожайности зерновых культур.

фактический ряд;

сглаженный ряд по пятилетним данным.

Недостатком сглаживания ряда является его «укорачивание» по сравнению с фактическим, а, следовательно, потеря информации.

Рассмотренные выше методы выравнивания динамического ряда дают возможность определить лишь общую тенденцию развития явления. Однако получить обобщенную статистическую модель посредством этих методов нельзя.

Количественную модель, выражающую основную тенденцию изменения уровней динамического ряда, можно с помощью метода аналитического выравнивания. Основным содержанием этого метода является то, что общая тенденция развития рассчитывается как функция времени:

у_t=f(t), где

у_t – уровни динамического ряда, вычисленные по аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и основывается на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики. Модели могут быть:

- линейная функция – прямая у_t=а₀+а₁ t, где

а_0, а₁ - параметры уравнения;

t – время.

- показательная функция - у_t=а₀^.а₁ t

- степенная функция – кривая второго порядка (парабола) - у_t=а₀+а₁ t+а₂ t²

Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения берется точка минимума суммы квадратов отклонений между теоретическими и эмпирическими уровнями:

∑( у_t- у_i)²→min, где

у_t – выровненные уровни;

у_i – фактические уровни.

Рассмотрим выравнивание динамического ряда по прямой: у_t=а₀+а₁ t. Параметры а_0, а₁ согласно методу наименьших квадратов находятся решением системы нормальных уравнений путем алгебраического преобразования условия ∑( у_t- у_i)²→min:

Расчет параметров упрощается, если за начало отсчета времени (t=0) принять центральный интервал (момент).

При нечетном числе уровней (например, 4), значения t будут такими:

2000 г. 2001 г. 2002 г. 2003 г.

-3 -1 +1 +3

При четном числе уровней (например, 5) значения устанавливаются по - другому:

2000 г. 2001 г. 2002 г. 2003 г. 2004 г.

-2 -1 0 +1 +2

В обоих случаях ∑t=0, так что система нормальных уравнений принимает вид:

Отсюда

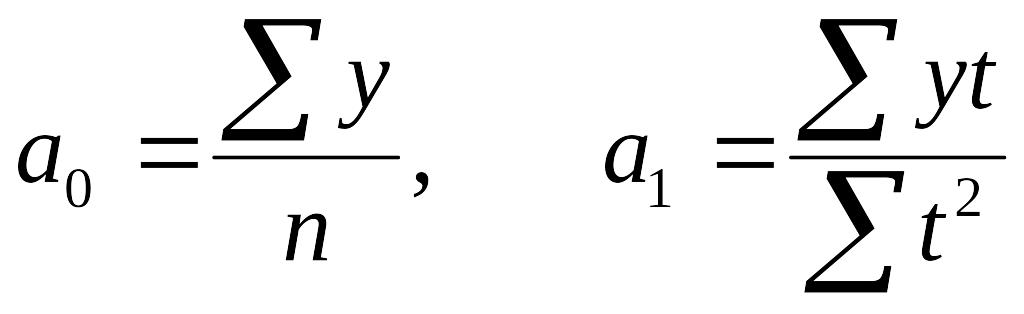
Выравнивание динамического ряда произведем на примере урожайности зерновых по Республике Татарстан (таблица 6.4.4)

Таблица 6.4.4. Выравнивание урожайности зерновых культур.

годы	Урожайность, ц/га	t	t2	уt	уt=26,7+0,4 t
1999	16,2	-2	4	-32,4	25,9
2000	21,3	-1	1	-21,3	26,3
2001	32,3	0	0	0	26,7
2002	32,0	1	1	32,0	27,1
2003	31,5	2	4	63,0	27,5
ИТОГО	133,3	0	10	41,3	133,5

Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: у_t=26,7+0,4 t.

Подставляя в это уравнение последовательно значения t, равные -2,-1, 0,+1,+2, находим выровненные уровни у_t.

Если расчеты выполнены правильно, то ∑у_i=∑у_t. В нашем примере небольшое расхождение за счет округления значений параметров а_0, и а₁ .

Полученное уравнение показывает, что несмотря на колебания урожайности зерновых по годам, в целом наблюдается тенденция ее увеличения.

а₀ характеризует среднюю урожайность зерновых в рассматриваемый период времени, а₁ - среднее ежегодное изменение урожайности. Так, с 1999 по 2003 гг. средняя урожайность зерновых составила 26,7 ц/га, в среднем ежегодно за этот период она росла на 0,4 ц/га.

Изобразим графически фактический ряд динамики урожайности зерновых и выровненный ряд.

Рис. 6.4.2 Фактический и выровненный динамический ряд урожайности зерновых культур.