5.2.2 Средняя гармоническая

Средняя гармоническая используется в тех случаях когда неизвестны частоты по отдельным вариантам, но есть данные о произведении каждой варианты на ее частоту (х_i f_i). Тогда и формулу средней арифметической взвешенной преобразуем так, чтобы по имеющимся данным х_i и х_i f_i можно было исчислить среднюю:

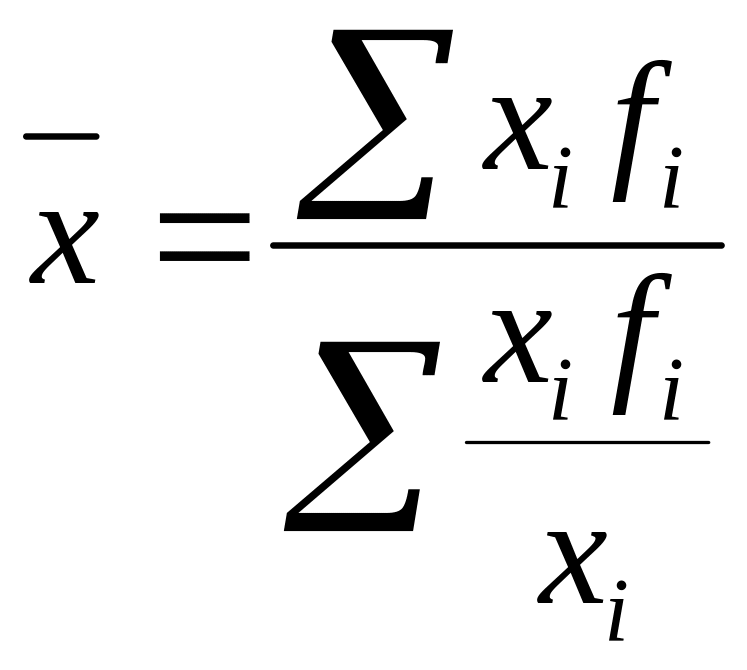
Из формулы видно, что средняя гармоническая – средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.

Например, по данным таблицы 5.2.3 требуется определить среднюю урожайность зерновых культур:

Таблица 5.2.3 Урожайность и валовой сбор зерновых культур

Культуры	Исходные данные		Расчетные данные
	Урожайность с 1 га, ц	Валовой сбор, ц	Посевная площадь, га
	хi	хi fi	fi
Пшеница озимая	28	5600	200
Пшеница яровая	25	3750	150
Рожь	18	1800	100
Ячмень	24	1920	80
Просо	15	1050	70
ИТОГО	-	14120	600

Урожайность определяется путем деления валового сбора на посевную площадь. Но размер посевной площади неизвестен. Его можно определить путем деления валового сбора по каждой культуре на урожайность данной культуры.

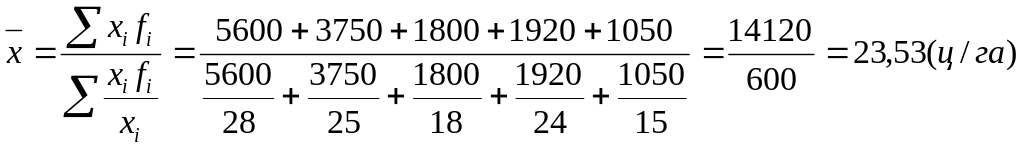
Средняя урожайность по зерновым культурам составит 23,53 ц/га.

В данном случае валовой сбор является определяющим показателем, связанным с осредняемым. Сумма произведений урожайности каждой культуры на ее посевную площадь равна произведению средней урожайности на общую посевную площадь:

или

Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого явления.

В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:

Например, четыре швеи - надомницы заняты пошивом головных уборов одной модели. Первая тратит на изготовление одного головного убора 30 мин., вторая -40, третья – 50, четвертая – 60 мин. Необходимо определить средние затраты на пошив одного головного убора при условии, что каждая надомница работает по 10 часов в день.

Если бы каждая надомница шила в день по одному головному убору, то средние затраты времени можно было бы определить по средней арифметической простой:

мин.

Но в данном случае средние затраты на пошив одного головного убора можно подсчитать путем деления общих затрат времени на количество сшитых головных уборов.

Количество сшитых головных уборов каждой надомницей равно: 1) 600:30=20 шт.;2) 600:40=15 шт.; 3) 600:50=12 шт.; 4) 600:60=10 шт.

Средние затраты вычислим по формуле средней гармонической взвешенной:

мин.

То есть на пошив одного головного убора в среднем затрачивается 42 мин.

В качестве веса здесь был принят показатель общих затрат времени на пошив всех головных уборов одной надомницей. Так как общие затраты у всех надомниц одинаковые, то к аналогичному результату приводит и расчет по средней гармонической простой:

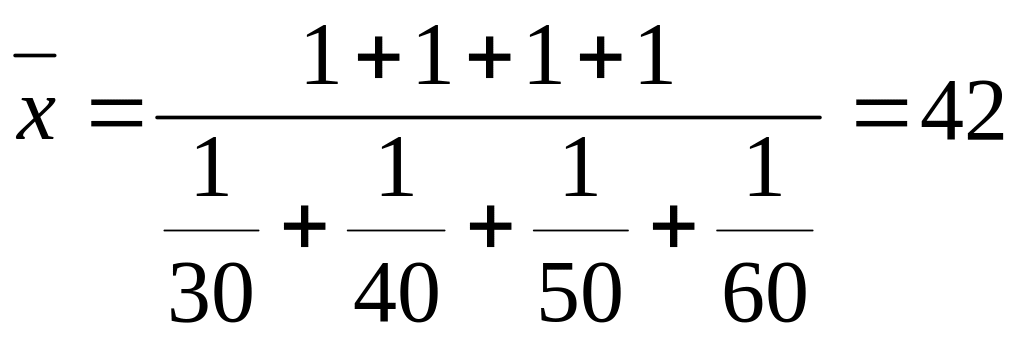мин.