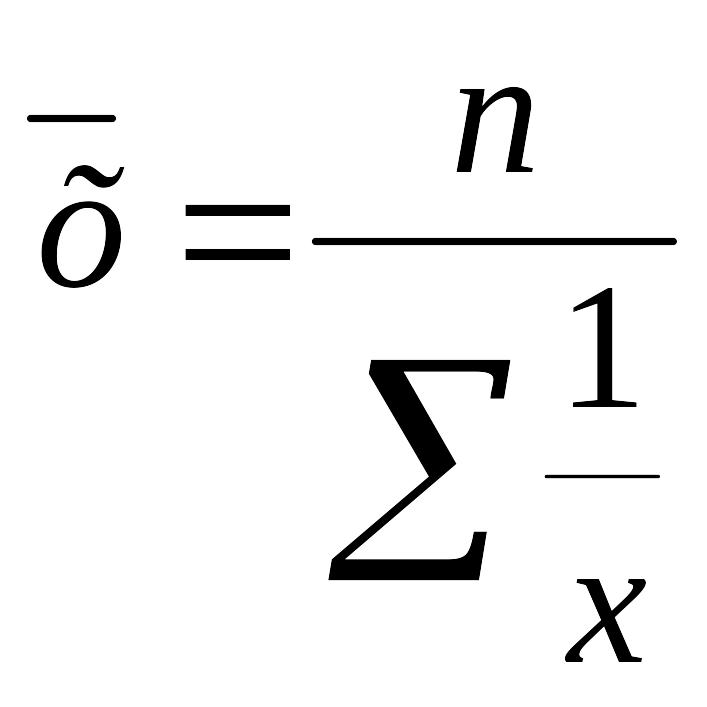2. Виды средних и способы их исчисления

Средние величины делятся на два больших класса:

1. степенные средние (средняя арифметическая, средняя

геометрическая и др.)

2. структурные средние (мода, медиана, квартили, децили,перцентили).

Степенные средние в зависимости от представления исходных данных исчисляются в двух формах: простой и взвешенной. Простая средняя считается по несгруппированным данным и имеет следующий вид:

, где

х_i – варианта (значение) осредняемого признака;

m – показатель степени средней

n – число вариант

Взвешенная средняя считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения:

, где

х_i – варианты (значение) осредняемого признака или серединное значение интервала, в котором изменяется варианта;

m – показатель степени средней;

- частота, показывающая, сколько раз встречается i –е значение осредняемого признака.

Таблица 5.2.1 Виды степенных средних величин

Вид степенной средней	Показатель степени (т)	Формула расчета
		Простая	Взвешенная
Гармоническая	-1
Геометрическая	→0
Арифметическая	1
Квадратическая	2
Кубическая	3

Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:

средняя гармоническая, если m = -1;

средняя геометрическая, если m 0;

средняя арифметическая, если m = 1;

средняя квадратическая, если m = 2;

средняя кубическая, если m = 3 и т.д.

Формулы средних степенных приведены в таблице 5.2.1.

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

_гарм.≤ _геом.≤ _арифм.≤ _квадр.≤ _куб.

Выбор средней определяется экономическим содержанием определенного показателя и исходных данных. Поэтому сначала необходимо построить логическую формулу расчета осредняемого показателя. Например,

Стоимость товарной продукции, тыс.руб.

Фондоотдача = Стоимость основных производственных фондов,тыс.руб.

Урожайность =

Размер вклада = и т.д.

1. Средняя арифметическая

Наиболее распространенный вид средней – средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Так, общий фонд заработной платы – это сумма заработных плат всех работников, валовой сбор урожая – сумма произведенной продукции со всей посевной площади.

Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений. Она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака.

Например: имеются данные о производстве продукции семью рабочими бригады за смену:

Номер рабочего	1	2	3	4	5	6	7
Произведено за смену, шт. хi	21	18	22	20	19	24	23

Необходимо определить среднюю выработку одного рабочего данной бригады:

(шт.)

В среднем за смену каждый рабочий производит 21 шт. изделия.

Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности.

Средняя арифметическая взвешенная – средняя сгруппированных величин х₁, х₂ … , х_n – вычисляется по формуле:

где f₁, f₂, …. f₃ – веса, частоты, повторения одинаковых признаков;

- сумма произведений величины признаков на их частоты;

- общая численность единиц совокупности.

Например, дано распределение рабочих бригады по выработке деталей:

Выработка деталей за смену одним рабочим, шт хi	18	19	20	21	22
Число рабочих, чел fi	2	4	5	3	1

Определить среднюю выработку за смену одним рабочим.

(шт.)

В среднем один рабочий за смену производит 20 шт. деталей.

В отдельных случаях веса могут быть представлены не абсолютными, а относительными величинами (в процентах или долях единицы). Тогда формула средней арифметической взвешенной будет иметь вид:

,

где - частость, т.е. доля каждой частоты в общей сумме частот.

Если частоты подсчитывают в долях (коэффициентах), то d=1 и формула средней арифметической взвешенной имеет вид:

,

Например, имеется следующее распределение рабочих по квалификации:

Квалификационный разряд	2	3	4	5	6
Число рабочих от общей численности (в долях)	0,15	0,25	0,30	0,20	0,10

Определить средний квалификационный разряд рабочих.

разряд

Средний квалификационный разряд рабочих данного коллектива составляет 4 разряд.

При расчете средней арифметической взвешенной в интервальном ряду распределения сначала определяют середину каждого интервала. Если интервалы открытые, то их величину условно приравнивают к интервалам, примыкающим к ним. Таким образом, от интервального переходят к дискретному ряду распределения путем замены интервальных значений их средними значениями и средние вычисляют как в дискретном ряду распределения.

Рассмотрим следующий пример (таблица 5.2.2).

Таблица 5.2.2 Распределение рабочих по уровню оплаты труда.

Месячная заработная плата , руб	Число рабочих, чел	Середина интервала, хi	хi fi
8000-8500	10	8250	82500
8500-9000	20	8750	175000
9000-9500	48	9250	444000
9500-10000	60	9750	585000
10000 и выше	62	10250	635500
ИТОГО	200	-	1922000

руб.

Итак, средний уровень оплаты труда рабочих составляет 9610 рублей в месяц.