Лекция №29

Тема: Катушка с ферромагнитным сердечником и трансформаторы

1. Катушка с ферромагнитным сердечником.

2. Трансформаторы. Режимы работы трансформаторов.

Катушка с ферромагнитным сердечником

Основой большинства электрических машин и аппаратов являются катушки с ферромагнитным сердечником (дроссель). Материал сердечника - электротехнические стали и другие ферромагнитные материалы (пермаллой, ферриты).

Предположим, что катушка с ферромагнитным сердечником присоединена к источнику с напряжением и (рис. 29.1).

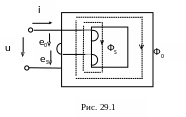При протекании по обмотке тока i создается переменный магнитный поток, часть которого (Ф₀) замыкается по сердечнику, а другая его часть (Ф_S) частично замыкается по воздуху. Поток Ф₀ называется основным потоком, а поток Ф_S - поток рассеяния.

Основной поток наводит в обмотке ЭДС самоиндукции:

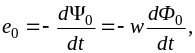а поток рассеяния ЭДС рассеяния:

Выберем на схеме положительные направления ЭДС e₀ и e_S. Если обозначить активное сопротивление обмотки через R, то, используя закон Ома для участка цепи можно написать:

u + e₀ + e_S =iR;

u = iR - e₀ - e_S = iR + 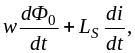- полное уравнение электрического состояния обмотки.

Или u = u_а +u₀ + u_S.

Катушка с ферромагнитным сердечником является нелинейным элементом, поэтому в общем случае, даже при синусоидальном напряжении u ,ток, магнитный поток и ЭДС являются величинами несинусоидальными.

Применим метод эквивалентных синусоид, положив тем самым, что ток, магнитный поток и ЭДС являются величинами синусоидальными, а их действующие значения равны действующим значениям несинусоидальных величин. Это позволяет использовать векторные диаграммы и уравнения электрического состояния в комплексной форме.

.

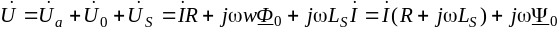В соответствии с этим уравнением катушку с ферромагнитным сердечником можно представить эквивалентной схемой (рис. 29.2),

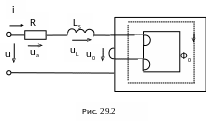где R - активное сопротивление катушки, L_S - индуктивность рассеяния. Сама катушка изображена обмоткой, помещенной на сердечнике и имеющей число витков w. Считается, что основной поток замыкается по сердечнику, а поток рассеяния отсутствует.

Мощность, поступающая в цепь катушки, частично расходуется на нагрев проводов обмотки, а частично на перемагничивание сердечника (потери на гистерезис) и на нагрев сердечника (потери на вихревые токи). Все перечисленные потери являются активными.

Эквивалентная схема отражает этот процесс: активное сопротивление R характеризует потери в меди, а активные потери мощности в сердечнике (потери в стали) отражены ферромагнитным сердечником с идеальной обмоткой. Из-за активных потерь в сердечнике ток в идеальной катушке будет отставать от напряжения на зажимах этой катушки на угол ₀.

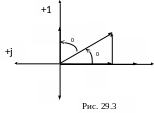
Векторная диаграмма идеальной катушки представлена на рис. 29.3.

Разложим вектор тока на составляющие 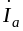и :

.

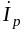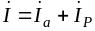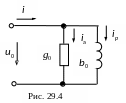Представим идеальную катушку эквивалентной схемой (рис. 29.4).

Проводимость g₀ характеризует активные потери в стали (на гистерезис и вихревые токи)

Р_ст = U₀Icos ₀ = U₀I_a = U₀²g₀,

а реактивная проводимость b₀ - характеризует основной магнитный поток Ф₀, замыкающийся по сердечнику и реактивную мощность

Q_ст = U₀Isin ₀ = U₀I_p = U₀²b₀.

Таким образом, катушку с ферромагнитным сердечником можно представить в виде эквивалентной схемы, где все элементы являются линейными для мгновенных значений напряжения и тока (рис. 29.5). а) параллельная схема; б) последовательная схема.

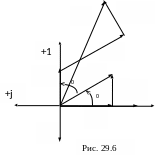
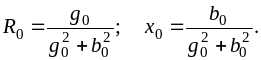
Векторная диаграмма представлена на рис. 29.6