Задача Штурма-Ліувілля

Знайти такі значення параметра , при яких рівняння

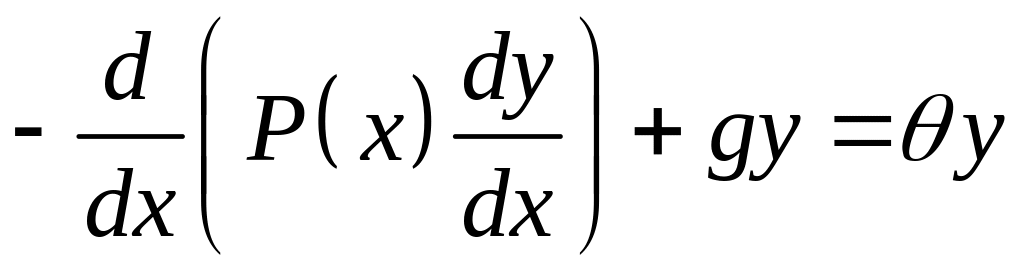(4.80)

має нетривіальні розв’язки , що задовольняють граничним умовам

(4.81)

, де

або в операторній формі рівняння (4.80) має вигляд. Умови (4.81) – це однорідні умови, що визначають лінійну комбінацію функції та її похідної на границі області. Задача (4.80) – (4.81) це повністю однорідна крайова задача з параметром . Тут маємо однорідне рівняння і однорідні крайові умови. Задачу (4.80) – (4.81) називають задачею Штурма-Ліувілля. Її ще називають задачею про власні функції.

Задача Штурма-Ліувілля у залежності від значень коефіцієнтів має різний фізичний зміст.

Якщо , то маємо крайові умови першого роду

, (4.82)

Якщо , то маємо крайові умови другого роду

, (4.83)

Якщо , то маємо загальні крайові умови або умови третього роду

, (4.84)

Так як у правих частинах умов (4.82)-(4.84) нулі, то усі умови однорідні. У більш загальному випадку у правій частині умов (4.82)-(4.84) замість нуля може стояти число або функція і тоді це будуть неоднорідні крайові умови.

Приклад 4.4

Знайти власні значення та власні функції задачі Штурма – Ліувілля для рівняння

,

що задовольняють наступним граничним умовам:

1. .

Загальний розв’язок рівняння має вигляд

Підставляємо граничні умови та отримуємо власні значення. Згідно з властивостями, власні значення повинні бути додатними

;

;

.

Власні функції

.

2. ;

;

.

Отже .

3. ,

,

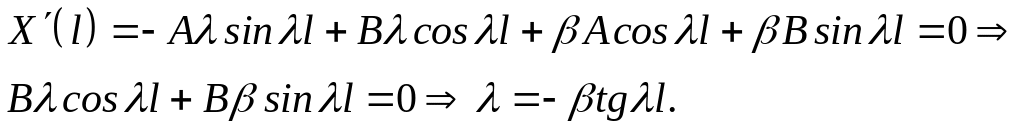
Власні значення визначаються як розв’язки трансцендентного рівняння

.

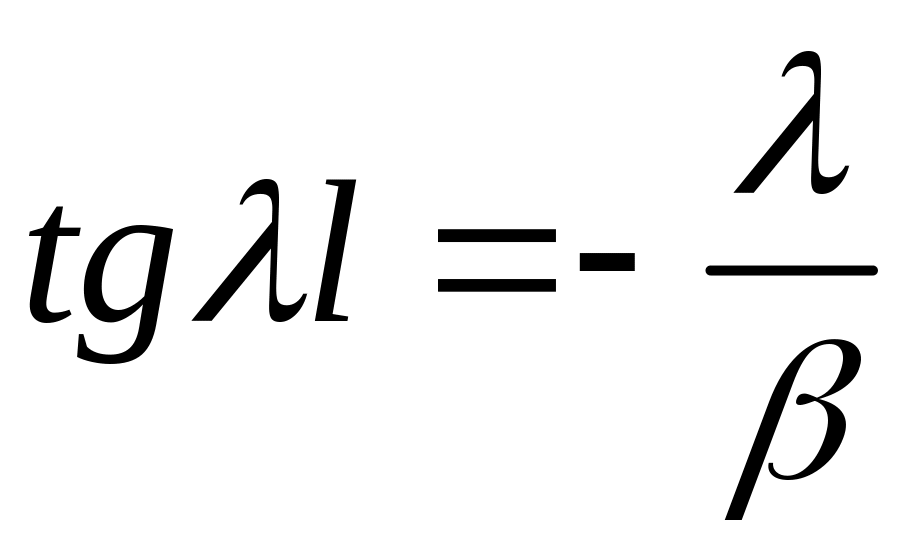Будуємо два графіки

та .

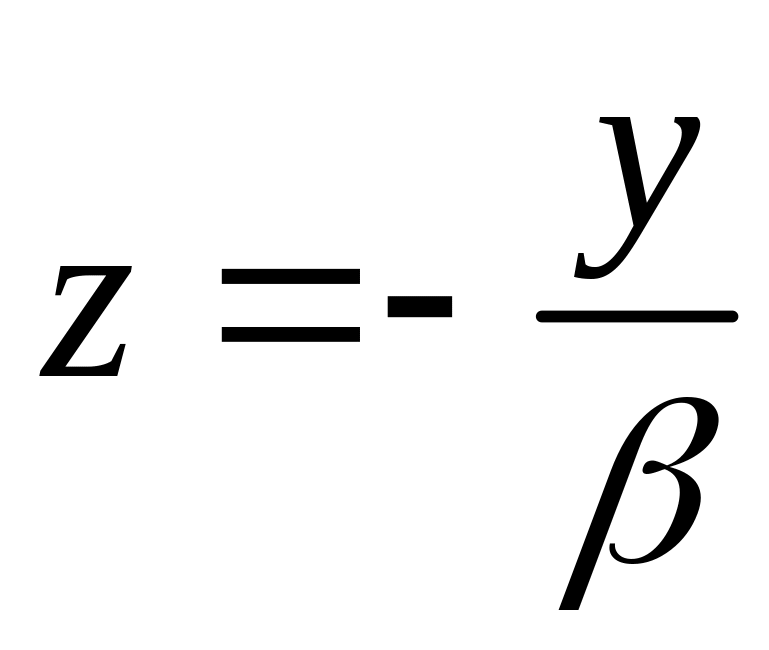Точки перетину цих графіків і будуть власними значеннями задачі.

4. .

Це умова періодичності

, .

Для визначення власних значень розв’язуємо систему рівнянь

.

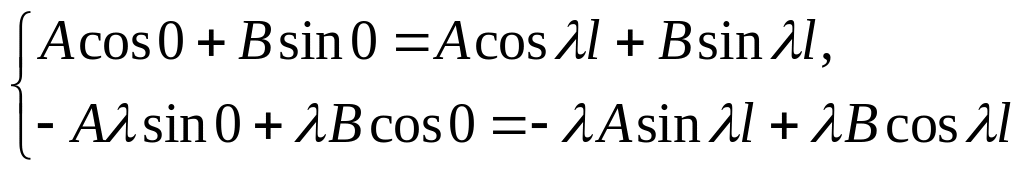Власні значення визначаються за формулами

,

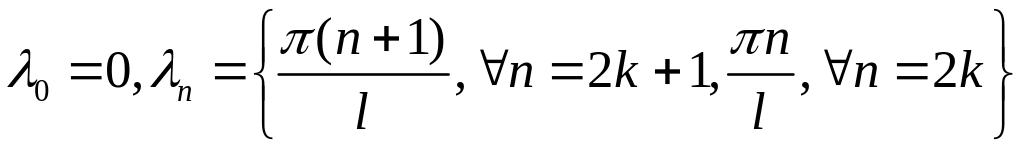а власні функції

.

Приклад 4.5 Знайти власні значення та власні функції задачі

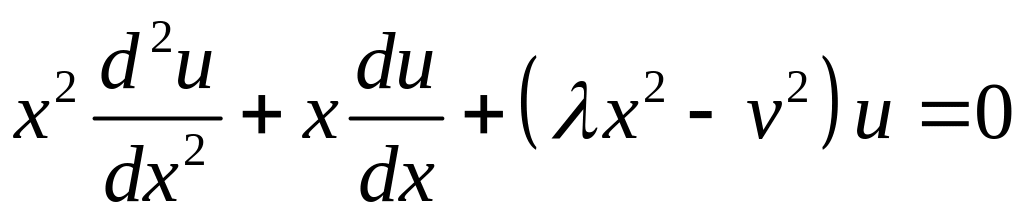, , (4.85)

, (4.86)

Слід зазначити, що не є власним значенням, оскільки із загального розв’язку рівняння (4.85) для

,

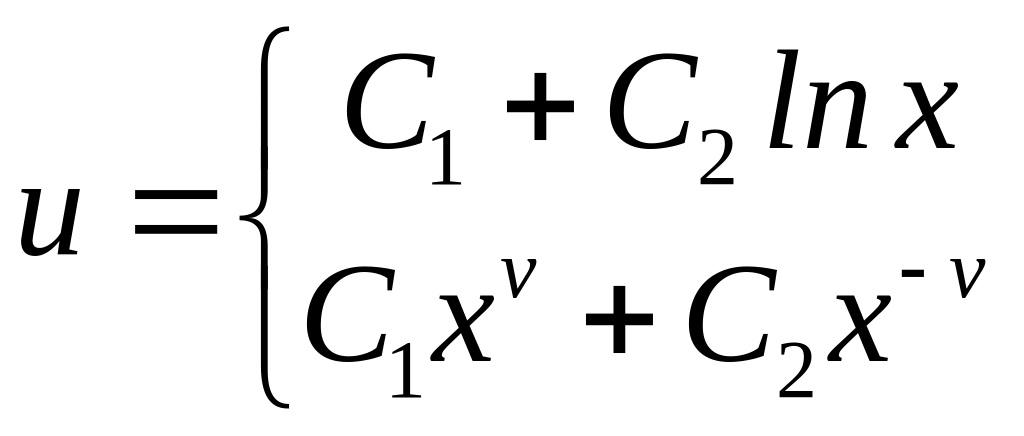із граничних умов (4.86) випливає, що задача має лише тривіальні розв’язки. Візьмемо і рівняння (4.85) перепишемо у вигляді

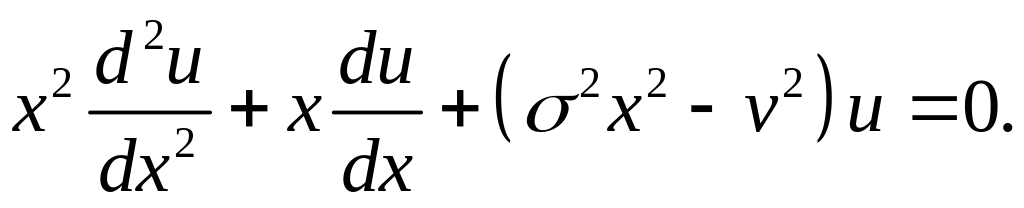(4.87)

Це – рівняння Бесселя і його загальний розв’язок має вигляд

(4.88)

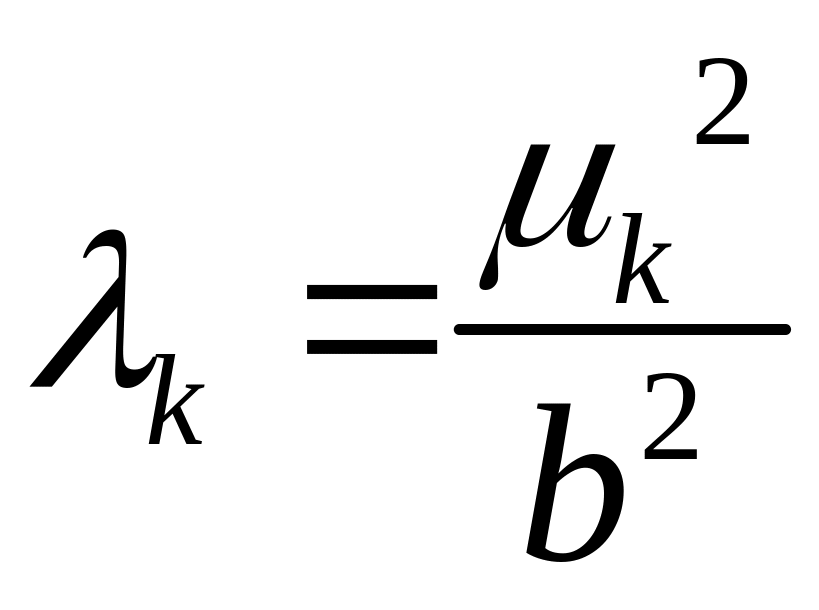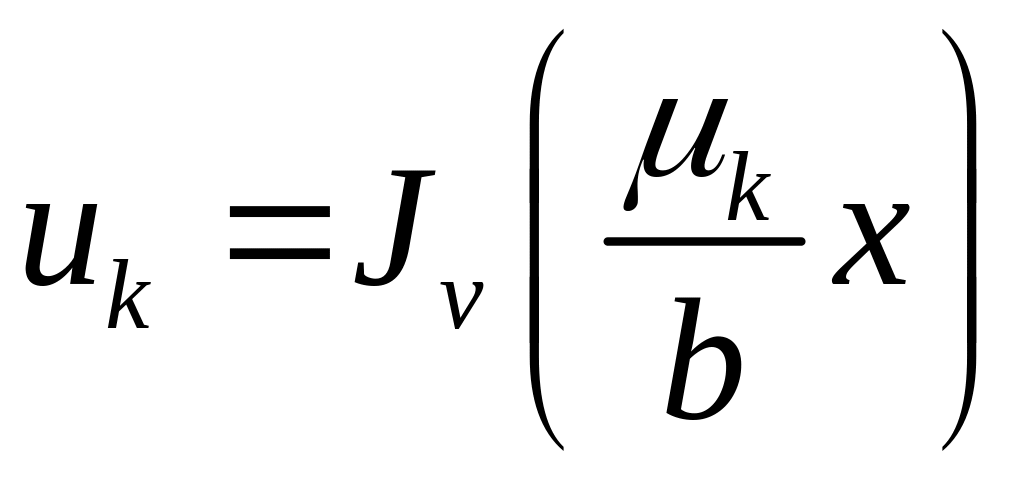Визначимо з крайових умов (4.86). Умова обмеженості розв’язку для приводить до того, що . Підставивши функцію до другої з умов (4.86), прийдемо до рівності . Оскільки , то . Отже, – додатний корінь рівняння . Тому власні значення цієї крайової задачі – , а власні функції – , ортогональні з вагою на відрізку .

4.6. Знайти власні значення та власні функції задачі 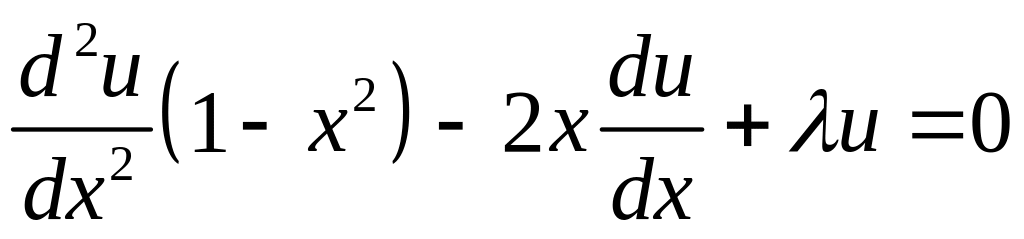, (4.89)

. (4.90)

Задача має власні значення , і відповідні їм власні функції , де – поліном Лежандра ступеня . Власні функції ортогональні на відрізку з вагою .

7. Знайти власні значення та власні функції задачі

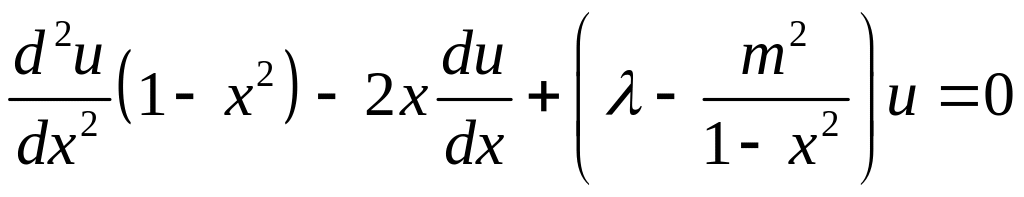, (4.91)

. (4.92)

Тут кожному власному числу , де відповідає лише одна власна функція . ( – приєднана функція Лежандра).