4.2 Теорема існування єдиного розв’язку першої крайової задачі

Теорема. Якщо виконуються умови:

1) функція та її частинні похідні до другого порядку включно за змінними та , а також похідна неперервні на відрізку для ,

2) коефіцієнти та функція неперервні на відрізку , то існує одна й тільки одна функція , визначена в області , що задовольняє рівнянню

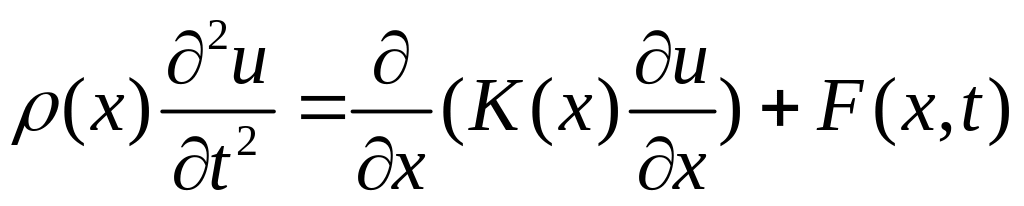, , (4.11)

,

початковим і граничним умовам

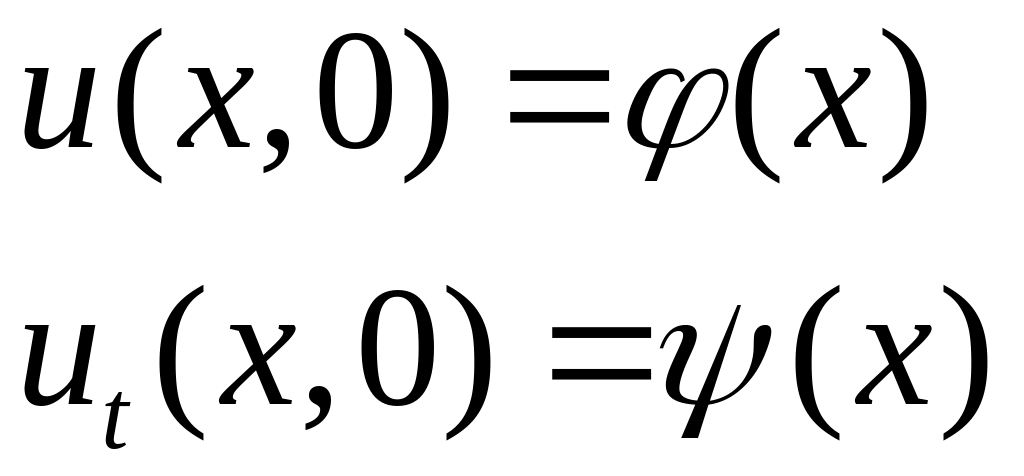, . (4.12)

Для доведення припустимо, що існують два розв’язки задачі (11)-(12) та . Розглянемо різницю . Функція , очевидно, задовольняє однорідному рівнянню

, (4.13)

і однорідним додатковим умовам , а також умові (4.12) теореми.

Доведемо, що функція .

Розглянемо функцію 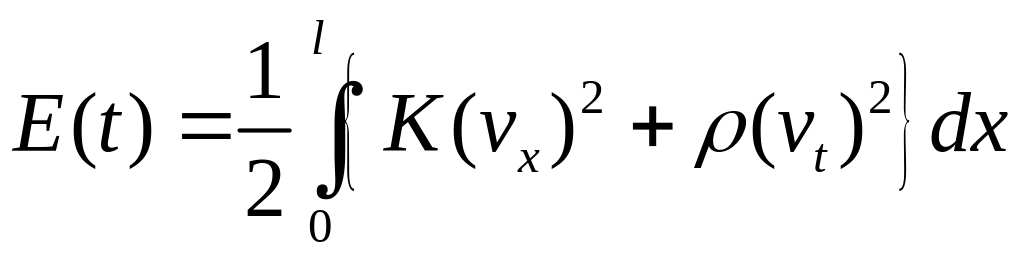, і покажемо, що вона не залежить від . Знайдемо похідну функції за змінною , виконуючи при цьому диференціювання під знаками інтеґрала

.

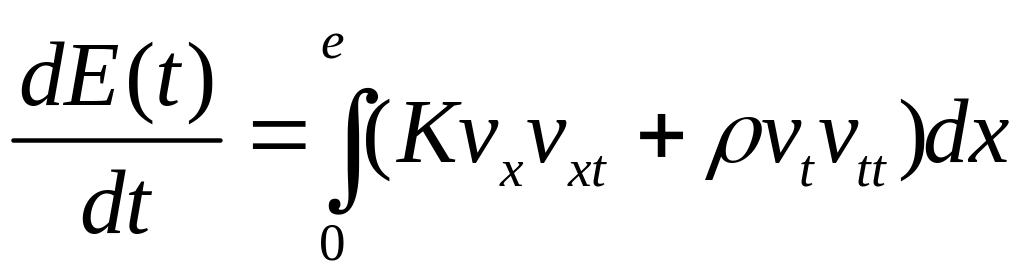Після інтеґрування частинами виразу, що стоїть під знаком інтеграла і підстановки граничних умов маємо

,

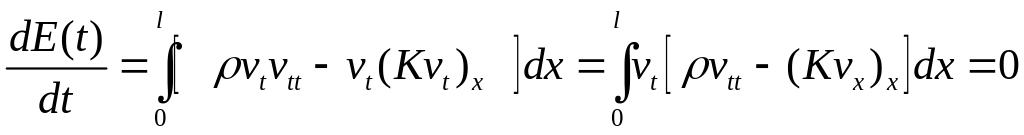тобто . Фізично означає повну енергію струни в момент часу t.

Ураховуючи початкову умову, отримаємо

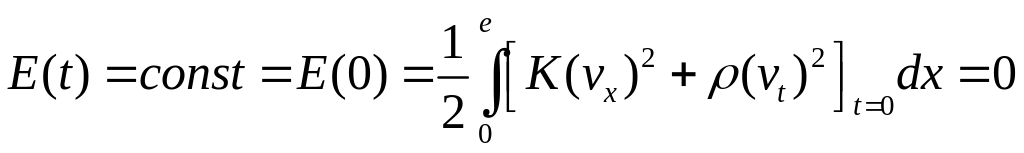. (4.14)

Використовуючи (4.14) і те, що функції і додатні, робимо висновок, що , . Звідки випливає, що . Враховуючи початкові умови, знаходимо , отже доведено, що .

У загальному випадку для мішаної задачі рівнянь гіперболічного типу

, , ,

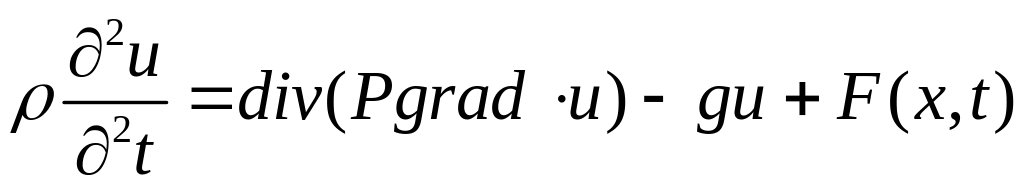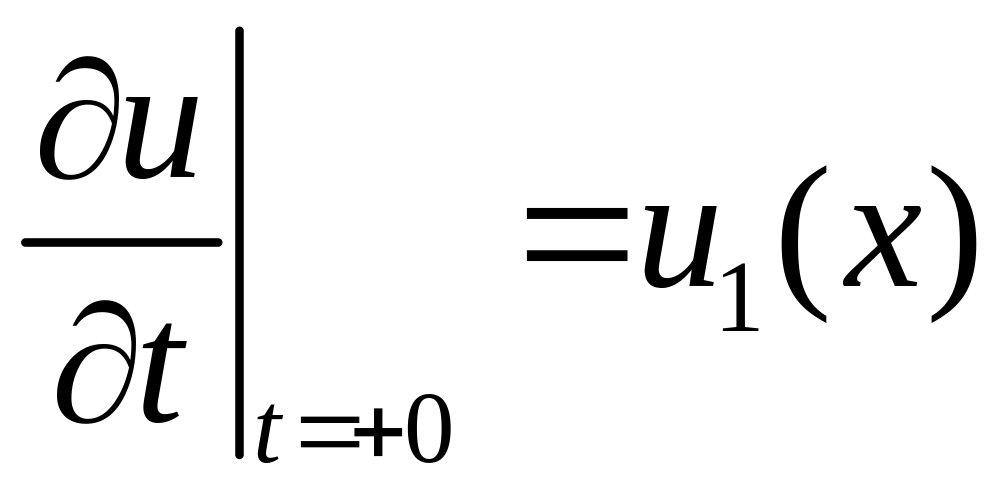, , , (4.15)

, .

інтеґралом енергії називається величина

,

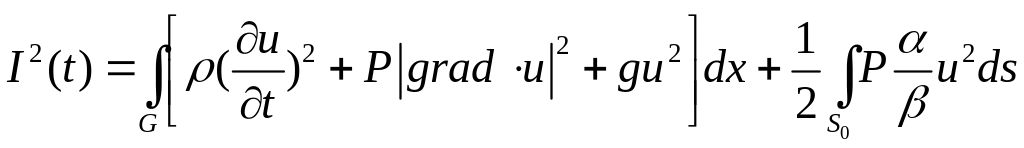яка представляє собою суму кінетичної та потенціальної енергії системи, що коливається в момент часу .

Якщо – класичний розв’язок задачі (4.15) і диференційована функція, тоді справедливе співвідношення:

, ,

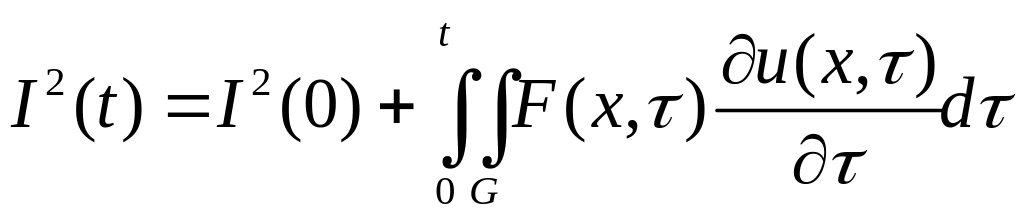де

.

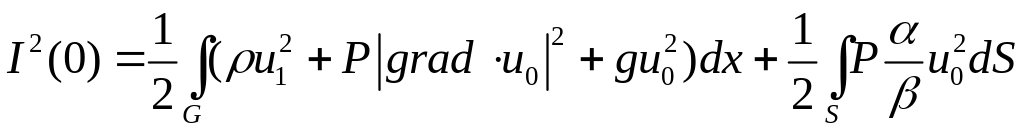4.3 Задача Коші для хвильового рівняння

Задача Коші для хвильового рівняння полягає у знаходженні розв’язку одного з рівнянь (4.4), (4.7), (4.9), що задовольняють лише початковим умовам.

Рівняння гіперболічного типу (4.4), (4.7), (4.9) описують процеси коливання.

Якщо вивчаються явища, що відбуваються за малі проміжки часу, то граничні умови відкидаються (слабо впливають) і задача переходить у задачу Коші

, ,

4.4 Метод д’Аламбера

Задача. Дослідити процес вільних коливань однорідної напівнескінченної струни, якщо початкове відхилення точок та їх початкова швидкість дорівнюють відповідно та .

Розв’язок. Це задача Коші. Для необмеженої струни рівняння коливань і початкові умови мають вигляд

, , , (4.16)

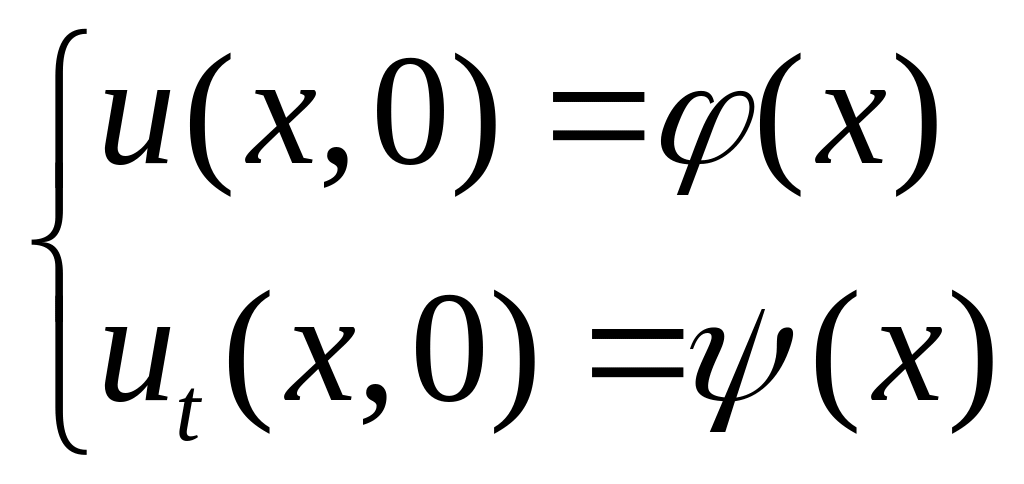, (4.17)

Перетворимо його до іншої канонічної форми з мішаною похідною.

Рівняння характеристик для рівняння (4.16) має вигляд

Воно розпадається на 2 рівняння

, .

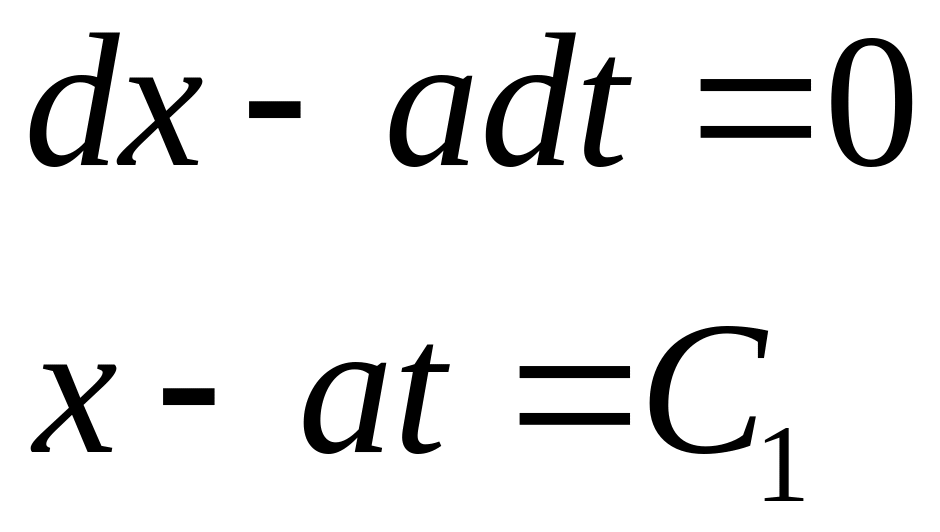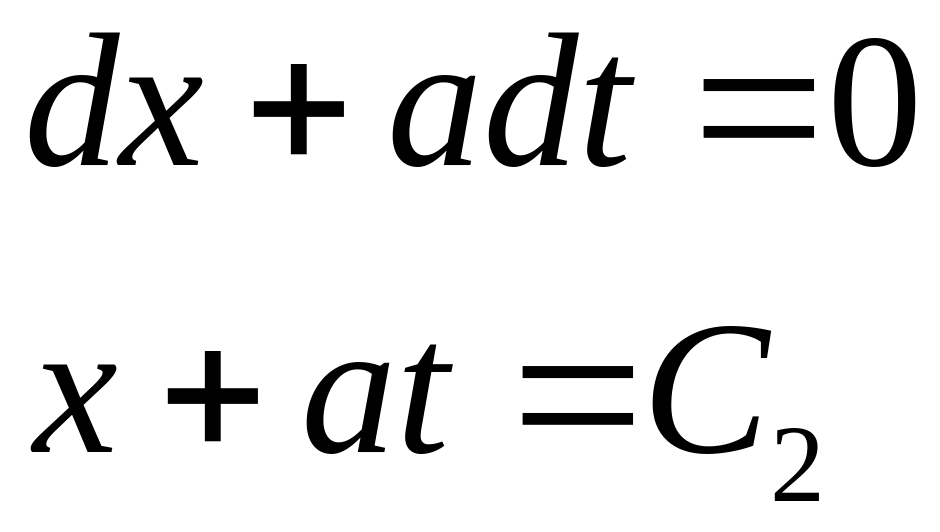Уведемо нові змінні .

Після перетворень

маємо рівняння .

Загальний інтеґрал цього рівняння має вигляд

. (4.18)

Отже, функція є загальним інтеґралом рівняння (4.16).

Визначимо і так , щоб вони задовольняли початковим умовам (4.17)

,

.

Інтеґруючи тут другу рівність, маємо

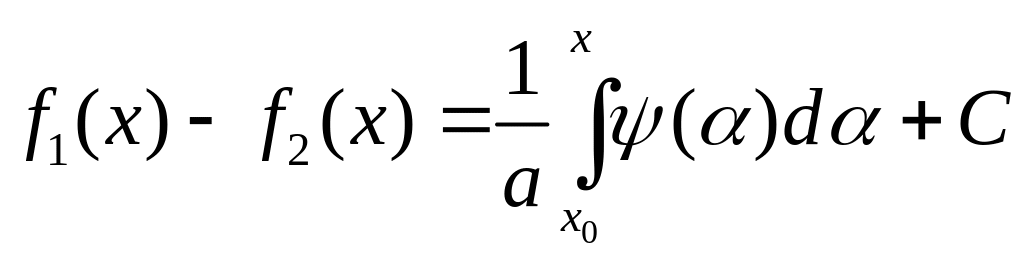. (4.19)

Звідси знайдемо

.

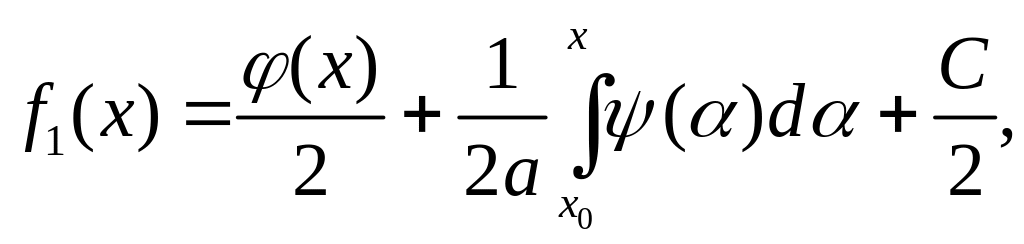
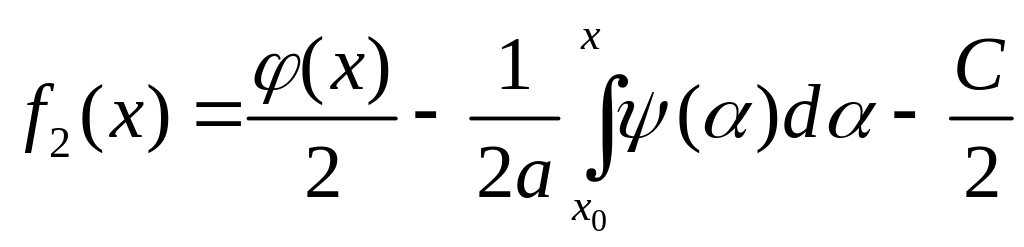Остання рівність справджується при будь-яких дійсних значеннях , а отже, вона буде справедлива і при заміні або при . Підставивши ці значення до рівняння, будемо мати

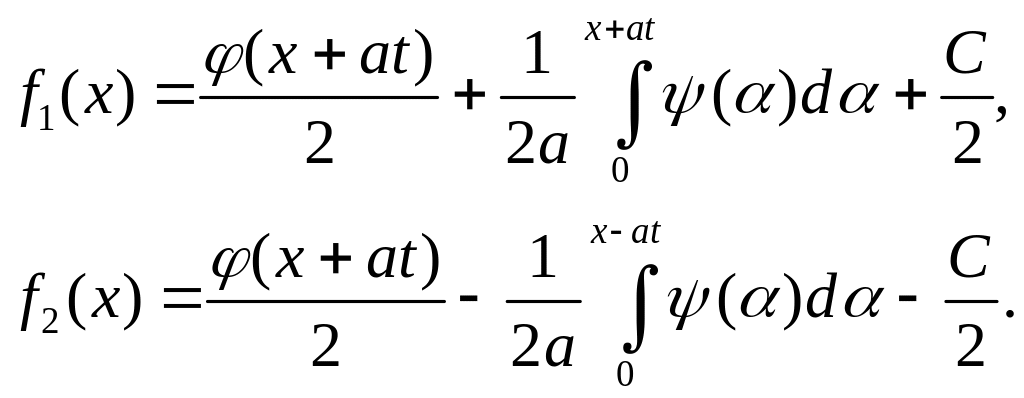
Додавши їх та враховуючи (4.18), будемо мати формулу Д’Aламбера для однорідного рівняння

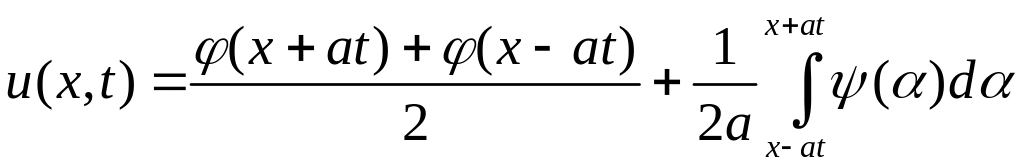. (4.20)

Отриманий метод свідчить про єдиність такого розв’язку задачі. З фізичної точки зору функція, що визначається формулою (4.20), описує процес розповсюдження початкового відхилення та початкової швидкості.

Розглянемо задачу Коші для неоднорідного рівняння

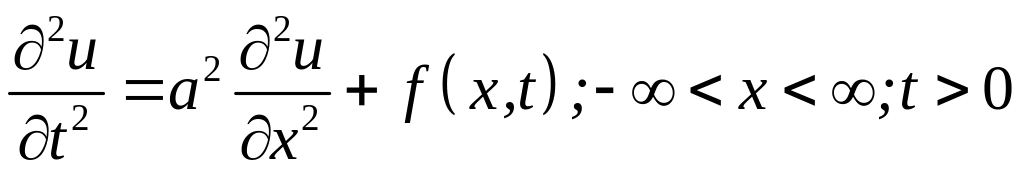(4.21)

(4.22)

Для знаходження її розв’язку задачу (4.21) , (4.22) розбиваємо на дві задачі

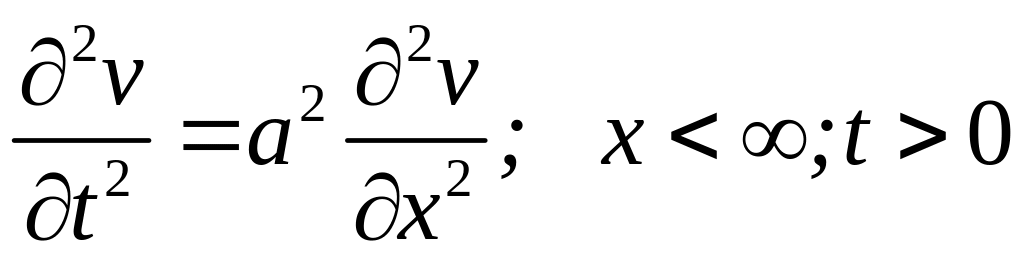(4.23)

(4.24)

та

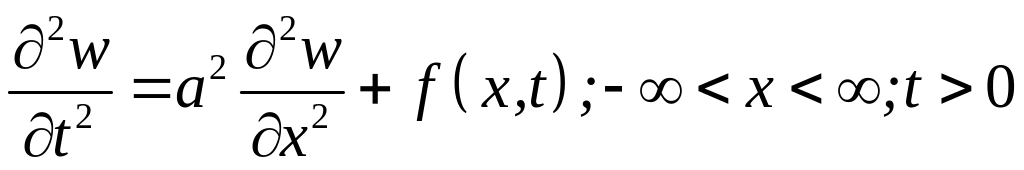(4.25)

(4.26)

Розв’язок задачі (4.21) , (4.22) шукаємо у вигляді суми

(4.27)

Розв’язок задачі (4.23), (4.24) за допомогою формули Д-Аламбера має вигляд

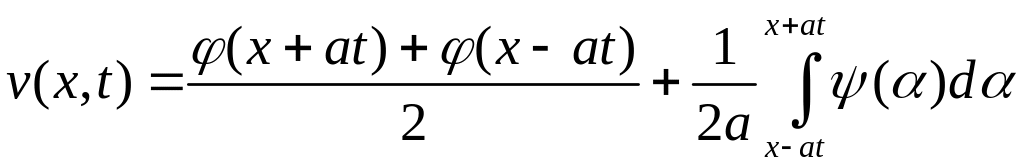
Для знаходження функції формулюємо допоміжну задачу

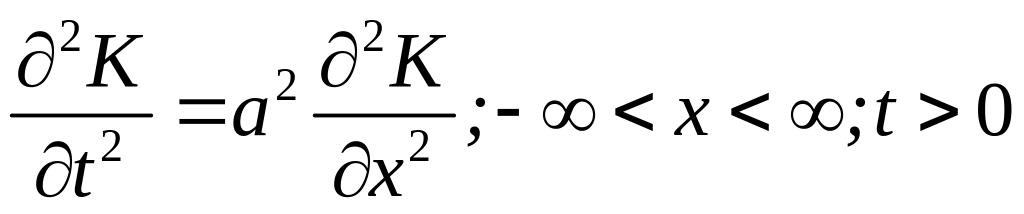
, - параметр (4.28)

При цьому 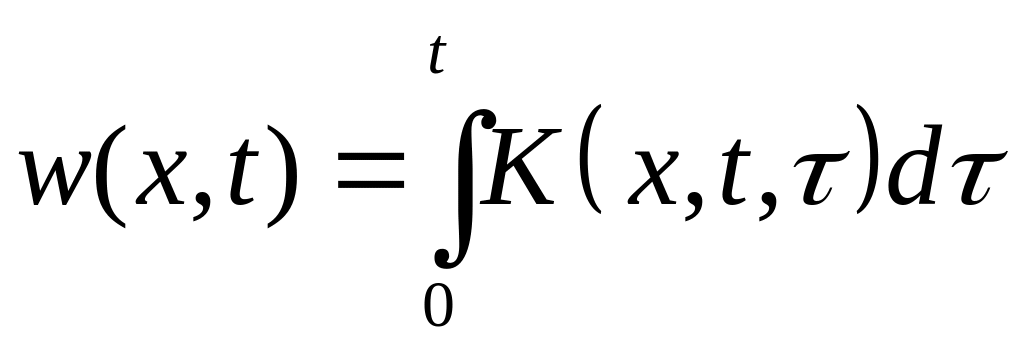. Функцію також знаходимо за формулою Д’Аламбера (4.20) у вигляді

,

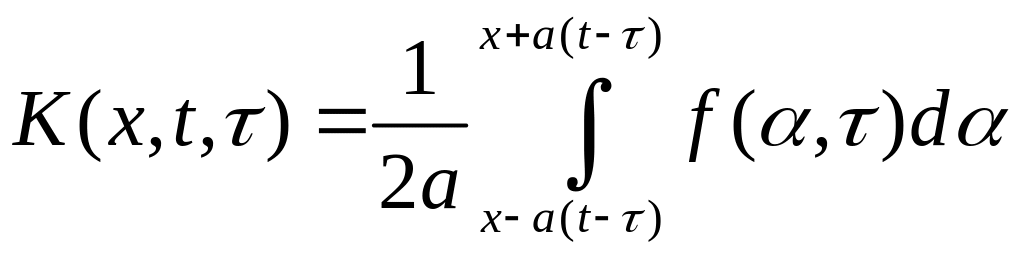а 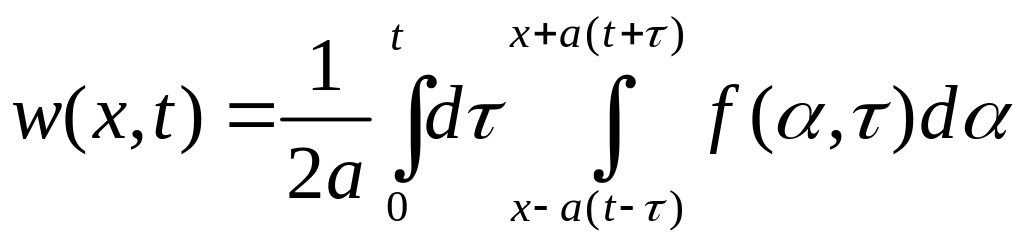(4.29)

Підставивши значення та у формулу (4.27) будемо мати

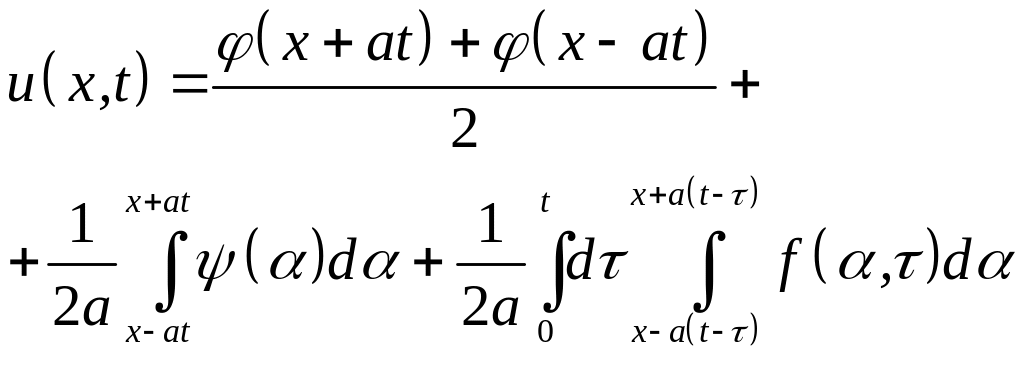(4.30)

Якщо існують похідні та , то це також є формула Д’Aламбера – розв’язок неоднорідного рівняння.

Приклад 4.1

Нехай в умовах задачі (4.16), (4.17) – ,а . Дослідити процес коливання струни.

Розв’язок. Підставивши замість та їх значення до формули (4.20), будемо мати

.