5. Расчетная интенсивность нагрузки

Наблюдениями установлено, что интенсивность нагрузки, создаваемой группой источников, колеблется по ЧНН разных дней. Поскольку зависимость вероятности потерь от интенсивности нагрузки имеет явно выраженный нелинейный характер, то в области малых значений потерь увеличение поступающей нагрузки всего на несколько процентов может привести к возрастанию потерь в несколько раз. При расчете объема оборудования с нормированными потерями р по математическому ожиданию нагрузки Y потери будут меньше или равны р только с вероятностью 0,5, т.е. в 50 % всех ЧНН. Если потребовать выполнения заданного качества обслуживания с большей вероятностью, то расчет объема оборудования следует выполнять не по математическому ожиданию интенсивности нагрузки, а по расчетной интенсивности нагрузки:

Y_p=Y + zσ(Y). (6.23)

где σ(Y) - среднеквадратическое отклонение интенсивности нагрузки в ЧНН.

Для простейшего потока вызовов математическое ожидание интенсивности нагрузки равно дисперсии нагрузки. Тогда полагая , получим следующее выражение для расчетной интенсивности нагрузки:

(6.24)

Коэффициент z характеризует степень гарантированности заданного качества обслуживания. В практике проектирования ГТС значение коэффициента z принимается равным 0,6742. При этом норма потерь р = 0,005 выполняется с вероятностью 0,75, а с вероятностью 0,9 потери не превысят 0,02, что для городской телефонной связи считается вполне приемлемым качеством обслуживания. Таким образом, формула расчетной интенсивности нагрузки имеет следующий вид:

. (6.25)

Переход от расчетного значения к математическому ожиданию нагрузки осуществляется по формуле

(6.26)

6. Системы обслуживания вызовов

6.1. Обслуживание вызовов системой с явными потерями

Одной из наиболее часто встречающихся задач в теории телетрафика является нахождение одного из трех параметров (обслуженная нагрузка, вероятность потерь и число каналов в пучке или обслуживающих устройств) при известных двух остальных. При обслуживании простейшего потока полнодоступной коммутационной системой с явными потерями вероятность потерь математически определяется с помощью первой формулы Эрланга. Условия, при которых возможно использование этой формулы, следующие:

• система обслуживания является системой с явными потерями, где сообщение и соответствующий ему вызов при получении отказа в немедленном соединении полностью теряются и на обслуживание больше не поступают (в реальных системах условные потери всегда присутствуют, однако при большом количестве источников ими можно пренебречь);

• система обслуживания является полнодоступной, где любому свободному входу доступен любой свободный выход;

• поток вызовов, поступающий на систему обслуживания, является случайным, где моменты поступления вызовов точно заранее не определены;

• число источников настолько велико, что последействием системы обслуживания можно пренебречь.

Следовательно, при обслуживании простейшего потока вызовов линиями полнодоступного пучка, которые включены в выходы коммутационной системы с потерями, вероятность того, что пучок находится в состоянии, когда все линии v заняты, определяется первой формулой Эрланга:

(6.27)

где Е - вероятность потерь; v - число линий (каналов) в пучке на выходе системы обслуживания; Y - нагрузка, обслуженная системой.

Например, E₅(2,7) означает вероятность потерь для системы с 5 выходами и обслуженной нагрузкой 2,7 Эрл. В этом случае вычисление по первой формуле Эрланга дает результат 0,085194 = 85‰. Где 85‰ – 85 промилле (одна тысячная доля, 1/10 процента и обозначается (‰)).

Функция табулирована. Таблицы первой формулы Эрланга позволяют по двум любым заданным величинам из v, Y и находить третью. В табл. 6.1 и на рис. 6.3 представлены табличный и графический, соответственно, способы определения потерь по вышеприведенному примеру.

Одним из условий применения первой формулы Эрланга является полнодоступность системы обслуживания. В случае использования неполнодоступных схем построения систем обслуживания вызовов используются другие методы расчета: метод О'Делла (для декадно-шаговых АТС), метод эффективной доступности (для координатных АТС), метод Вилкинсона (для вычисления потерь в сетях с альтернативной маршрутизацией) и др.

Таблица 6.1 Таблица потерь (первая формула Эрланга)

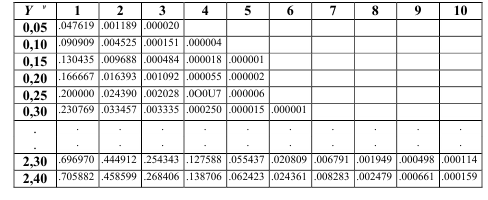
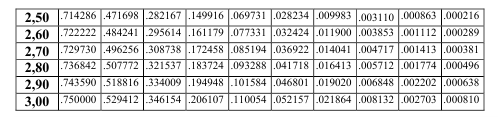
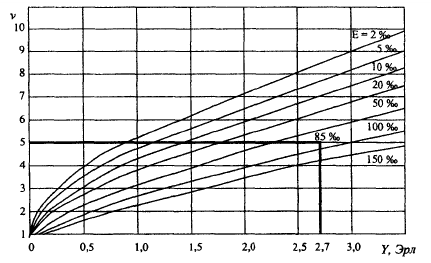
Рис. 6.3. График потерь (первая формула Эрланга)

В том случае когда число источников в системе с явными потерями не велико (например УПАТС малой емкости или мини-АТС), абоненты создают примитивный поток вызовов, а вероятность потерь по вызовам определяется с помощью формулы Энгсета:

(6.28)

где:

N - число источников вызовов; v - число линий (каналов), обслуживающих нагрузку;

а - интенсивность потока вызовов от одного свободного источника.

Формула Энгсета также табулирована. Таблицы позволяют по трем любым заданным величинам из v, а, р_в и N находить четвертую.