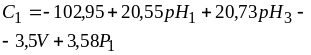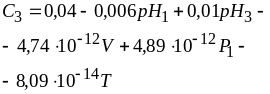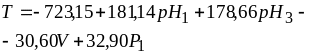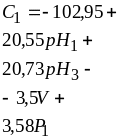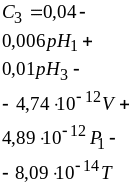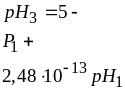Решение

Для получения количественных характеристик используем Excel. В Сервисе выбираем Анализ Данных. В открывшемся подменю выбираем Регрессия, заполняем поля, как указано на рис.3.7.

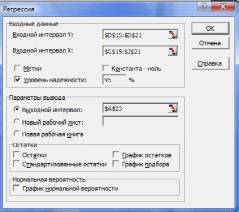
Рисунок 3.7. Заполнение полей при выполнении Анализа данных – Регрессия.

В результате получаем итоговые значения (табл.3.7)

Таблица 3.7

Регрессионная статистика

Регрессионная статистика
Множественный R	0,9971
R-квадрат	0,9942
Нормированный R-квадрат	0,9825
Стандартная ошибка	0,0317
Наблюдения	7

Регрессионную статистику используют для оценки информативности модели:

Множественный R (коэффициент множественной корреляции) - чем ближе он к 1, тем выше информативность модели. R² - представляет собой долю общей суммы квадратов, объясняемой моделью (Еще его называют коэффициентом детерминации):

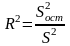. (3.17)

Его значение должно быть как можно ближе к единице. Эмпирически установлено, что для активного эксперимента оно должно быть не мене 0,96-0,97. Модель считается работоспособной при значении 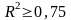. Это необходимое, не недостаточное условие. Достаточным условием является проверка значимости коэффициента множественной корреляции по критерию Фишера.

Для анализа адекватности необходима остаточная дисперсия и дисперсия воспроизводимости. Под адекватностью в целом подразумевают соответствие модели описываемому процессу или объекту по заранее определенным условиям. В частности в регрессионном анализе проверка адекватности сводится к проверке по критерию Фищера, принадлежности дисперсии воспроизводимости и остаточной дисперсии к одной генеральной совокупности ( формула 3.21). Если F_табл меньше F_расч, то модель считается адекватной с заданным уровнем значимости, при этом различие дисперсий статистически незначимо. Эта проверка является формальной, поэтому окончательное решение об адекватности модели следует принимать, исходя из пригодности модели к практическому применению по всей совокупности параметров.

Если нет параллельных опытов, то либо для моделей сравнивают остаточные дисперсии

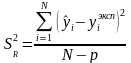, (3.18)

либо сравнивают эту величину с оценкой разброса опытных данных относительно среднего значения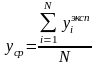 - дисперсии среднего

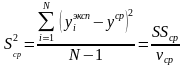. (3.19)

Так как последняя дисперсия больше 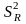, то для критерия Фишера рассматривают отношение 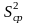к , и условие адекватности будет иметь вид

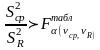. (3.20)

Некоторые авторы, в случае, когда повторные опыты отсутствуют, считают модель адекватной, если выполняется условие:

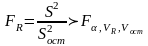(3.21)

V_R, V_ости- степени свободы для дисперсии, объясняемой моделью и остаточной дисперсией соответственно.

Если расчетное значение больше табличного с заданным уровнем значимости, том модель информативна. Такая проверка информативности является качественной.

Для определения значимости коэффициента множественной корреляции необходима дисперсия, объясняемая моделью, которая находится в ячейке на пересечении строки Регрессия и столбца МS, и остаточная дисперсия, которая находится в ячейке на пересечении строки Остаток и столбца МS (табл.3.8).

Таблица 3.8

Таблица дисперсионного анализа

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	4	0,341733067	0,085433267	85,01708079	0,011659385
Остаток	2	0,002009791	0,001004895
Итого	6	0,343742857

Расчетное значение критерия Фишера для оценки значимости множественного коэффициента регрессии находится в строке Регрессия и столбце F. Критическое значение вычисляют вызовом функции =FРАСПОБР(0,05;7-5;5-1), где 7 - число опытов, а 3 - число членов модели, которое равно 6,94. Поскольку это значение меньше расчетного, то множественной коэффициент регрессии значим.

Для построения уравнения регрессии используем конечную таблицу 3.9:

Таблица 3.9

Таблица характеристик переменных

	Коэффи-циенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-102,95	3E+06	-4E-05	0,99997	-1E+07	1E+07	-1E+07	1E+07
Переменная X 1	20,5513	524714	3,9E-05	0,99997	-2E+06	2E+06	-2E+06	2E+06
Переменная X 2	20,7271	524714	4E-05	0,99997	-2E+06	2E+06	-2E+06	2E+06
Переменная X 3	-3,5511	1,9916	-1,7831	0,21651	-12,12	5,0179	-12,12	5,018
Переменная X 4	3,57574	1,9638	1,82086	0,21023	-4,8737	12,025	-4,8737	12,03

Таблица коэффициентов регрессии и их статистических характеристик в первом столбце содержит названия коэффициентов, во втором - значение коэффициентов регрессии, затем стандартное отклонение для него и расчетное значение t-статистики. Под У-пересечением подразумевают свободный член. Регрессоры, для которых расчетное значение t-статистики меньше критического (табличное значение критерия Стьюдента с уровнем значимости α, и ν степенями свободы; при этом ν=(N(n-1) , где N - число экспериментов, а n - количество повторных опытов; вычисляют с помощью функции СТЬЮДРАСПРОБР) должны быть удалены из модели. Критическое значение критерия Стьюдента вычисляют вызовом функции = СТЬЮДРАСПОБР(0,05;7*(2-1)). Оно равно 2,36 (или см. табл. распределений Стьюдента, 2.36). Если расчетные значения коэффициентов регрессии больше этого числа, то они значимы. В нашем случае они незначимы.

Согласно таблице наша зависимость может быть описана как

или в наших характеристиках:

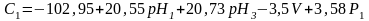
Даже без учета t-статистики и стандартной ошибки видно, что при описании влияния рассматриваемых факторов на концентрацию не учтены более существенные факторы, поскольку достаточно велико значение свободного члена. С определенной долей вероятности можно предположить существенное влияние на изменение концентрации рН (их вклад примерно одинаков) и значительно меньшее влияние объема и давления, которые сопоставимы между собой.

Аналогично получаем уравнения для других зависимостей, результаты котонных приведены в таблице 3.10.

Таблица 3.10

Таблица информативности модели

№ п/п	У	факторы	Уравнение	Fрасч	Fтабл
1	С1	рН1,рН3, V, Р1		85,02	6,94
2	С2	рН1,рН3, V, Р1		64,07	6,94
3	С3	рН1,рН3, V, Р1, Т,			6,61
4	Т	рН1,рН3, V, Р1		1,36	6,94
5	рН3	Р1, рН1			19,25
6	С1	рН1		305,14	230,16
7	С2	рН1		127,37	230,16
8	С3	рН1			230,16
9	С1	рН3		305,14	230,16
10	С2	рН3		127,37	230,16
11	С3	рН3			230,16
12	С1	V		8,69	230,16
13	С2	V		6,56	230,16
14	С3	V		10,05	230,16
15	С1	Р1		3,79	230,16
16	С2	Р1		2,86	230,16
17	С3	Р1		4,42	230,16
18	Р1	Т		6,45	230,16
19	V	Т		5,59	230,16
20	рН1	Т		4	230,16
21	С3	Т		2,14	230,16
22	рН3	Т		2,14	230,16
23	рН3	Р1		4,42	230,16
24	Р1	V		112,84	230,16
25	рН1	рН3			230,16

Итак,

1) проверка информативности модели дает следующие результаты (табл.3.11):

Таблица 3.11

Таблица информативных моделей

№ п/п	У	факторы	Уравнение	Fрасч	Fтабл
1	С1	рН1,рН3, V, Р1		85,02	6,94
2	С2	рН1,рН3, V, Р1		64,07	6,94
3	С3	рН1,рН3, V, Р1, Т,			6,61
5	рН3	Р1, рН1			19,25
6	С1	рН1		305,14	230,16
8	С3	рН1			230,16
9	С1	рН3		305,14	230,16
11	С3	рН3			230,16
25	рН1	рН3			230,16

2) для этих моделей определяем значимость коэффициентов регрессии (табл.3.12):

Таблица 3.12

Определение значимости коэффициентов регрессии

№ п/п	У	факторы	Уравнение	t-статистика	tP
1	С1	рН1,рН3, V, Р1		-4E-05 3,9E-05 4E-05 -1,7831 1,82086	2,36
2	С2	рН1,рН3, V, Р1		-5E-05 5,1E-05 5,1E-05 -2,3321 2,43788
3	С3	рН1,рН3, V, Р1, Т,		21446,1 -16337 34758,4 -0,9606 0,97127 -0,8122
5	рН3	Р1, рН1		1,3E+13 -3E+13 1,99481
6	С1	рН1		26,9587 -17,468
8	С3	рН1		8,9E+15 -4E+15
9	С1	рН3		-6,7571 17,4684
11	С3	рН3		2E+14 9,7E+14
25	рН1	рН3		8,5E+14 -4E+14

Проверка значимости коэффициентов регрессии показала незначимость коэффициентов регрессии уравнений 1; значимость коэффициента 5 в уравнении 2, но модель С2=f(P1) неинформативна; значимость коэффициентов 1,3 в модели 3, С2=f(рН3), которая исследована ниже; значимость коэффициентов 1,2 в уравнении 5, рН3=f(Р1), которая рассмотрена ниже; значимость всех коэффициентов в уравнениях 6, 8, 9, 11, 25.

Для использования количественных характеристик сопоставим данные аппроксимации и уравнения, полученные с помощью регрессионного анализа (табл.3.13).

Таблица 3.13

Сравнение уравнений, полученный при аппроксимации данных и регрессионным анализом

№ п/п	У	фактор	Уравнение (аппроксимация)	R2	Уравнение (регрессия)	R2	дисперсия
1	С1	рН1		1		0,98	0,03
2	С2	рН1		0,96
3	С3	рН1		1		1	6,20E-18
4	С1	рН3		1		0,98	0,03
5	С2	рН3		1
6	С3	рН3		1		1	2,705 E-17
7	С1	V	замена
	V	С1	y = -2381,6x5 + 7717,8x4 - 9743,2x3 + 5984,3x2 - 1789,9x + 212,34	1
8	С2	V	замена
	V	С2	y = -19,027x3 + 33,557x2 - 17,191x + 5,6024	0,98
9	С3	V	замена
	V	С3		1
10	С1	Р1	y = -4673,4x4 + 64656x3 - 335234x2 + 771997x - 666224	0,99
11	С2	Р1	замена
	Р1	С2	y = -426,4x4 + 1372,9x3 - 1656,9x2 + 888,11x - 174,75	1
12	С3	Р1	Замена
	Р1	С3		1
13	Р1	Т		1
14	V	Т		1
15	рН1	Т		1
16	С3	Т		1
17	рН3	Т		1
18	рН3	Р1	y = -9848,3x4 + 136268x3 - 706614x2 + 2E+06x - 1E+06	1
19	Р1	V	замена
	V	Р1		0,97
20	рН1	рН3		1		1	3,102 E-15

Итак, для анализа эксплуатации химико-технологической системы недостаточно проведения аппроксимации данных, но для выявления линейной связи, что характеризует процесс, определять вид зависимости необходимо. С другой стороны, хорошее совпадение моделей (у четом R-квадрата и дисперсионного рассеивания) позволяет делать надежные выводы.

В результате проделанной работы мы определили:

1. Увеличить концентрацию С1 и С3 можно уменьшая значение рН1, причем наиболее существенно влияние рН1 на С1.

2. Увеличить концентрацию С1 и С3 можно увеличивая значение рН3, причем наиболее существенно влияние рН3 на С1.

3. Процесс протекает в кислой среде, не выше 5. Для увеличения С1 сумма рН1 и рН2 должна быть равна 5.

4. рН1 и рН3 – величины математически зависимые. Увеличение рН1 приводит к снижению рН3.

5. Процесс следует вести регулируя рН3 для корректировки С1. При этом следует учитывать вызываемые этой корректировкой изменения С3. И наоборот.

6. Для управления процессом и получения оптимальных условий следует решить систему уравнений

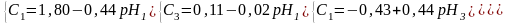
При граничном условии .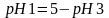

20