Регрессионный анализ

Обработка экспериментальных статистических данных при использова­нии корреляционного и регрессионного анализа дает возможность решить задачи построения математической модели в виде уравнения регрессии. При обработке эксперимента находят уравнение приближенной регрессии, оценивая при этом величину и вероятность этой приближенности. Задача ставится таким образом: по данной выборке объема n найти уравнение приближенной регрессии и оценить допускаемую при этом ошибку. Эта задача решается методами регрессионного и корреляционного анализа.

В общем случае можно рассматривать:

- зависимость выходной переменной от одного фактора или зависимость выходной переменной от нескольких факторов,

- линейные и нелинейные уравнения регрессии.

Преобразование системы координат y – x дает возможность выбрать оптимальный вид функциональной зависимости.

Исследование зависимости от одного фактора

При изучении зависимости от одного переменного параметра для определения вида уравнения регрессии рекомендуется построить эмпирическую линию регрессии. Для этого весь диапазон изменения х на поле корреляции (рис.3.1) разбивается на k равных интервалов - ∆х. Все точки, попавшие в данный интервал ∆х_j, относят к его середине х_j. Для этого подсчитывают частные средние 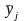для каждого интервала.

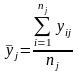, (3.1)

где n_j- число точек в интервале ∆х_j; при этом

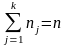; (3.2)

n-объем выборки. Затем последовательно соединяют точки (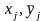 ) отрезками прямой. Полученная ломаная называется эмпирической линией регрессии y по х. По виду эмпирической линии регрессии подбираем уравнение регрессии у=f(х).

Пример 3.1. Построить эмпирическую линию регрессии изменения рН раствора при вводе коагулянта и определить уравнения регрессии. Данные приведены в табл.3.1.

Таблица 3.1

Изменения рН раствора при вводе коагулянта

мг/моль	0,02	0,02	0,02	0,03	0,03	0,03	0,04	0,04	0,04	0,05	0,05	0,05	0,06	0,06	0,06
рН	8,6	8,6	8,7	8,7	8,7	8,9	8,9	9,1	9,2	9,3	9,3	9,3	9,3	9,4	9,4

Решение

1. Наносим данные на поле в координатах коагулянт-рН.

На лист Excel заносим исходные данные табл.3.1. Выделяем мышью численные данные таблицы. В Мастере диаграмм выбираем Тип: Точечная, Позволяющая сравнивать пары значений. Полученный график приведен на рис.3.1.

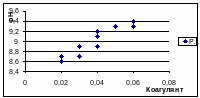
Рисунок 3.1. Исходные данные в поле координатах коагулянт-рН.

2. Определяем эмпирическую линию регрессии.

Строим ранжированный ряд по х используя Данные Сортировка (рис.3.2).

Рисунок 3.2. Выполнение сортировки данных.

Для этого весь диапазон изменения х (в нашем случае концентрации коагулянта) от 0,02 до 0,06 разбиваем на интервалы Δх - 0,01.

Подсчитываем частные средние для каждого интервала по формуле (3.5). Число точек в интервале ∆х_j в нашем примере равно 3. Полученные значения приведены в табл. 3.2.

Таблица 3.2

Частные средние для каждого интервала

мг/моль	0,02		0,02		0,02		0,03		0,03		0,03		0,04		0,04		0,04		0,05		0,05		0,05		0,06		0,06		0,06
рН	8,6		8,6		8,7		8,7		8,7		8,9		8,9		9,1		9,2		9,3		9,3		9,3		9,3		9,4		9,4
хj		0,02						0,03						0,04						0,05						0,06
	8,63						8,77						9,07						9,3						9,37

На листе Excel в поле Диаграммы в Исходные данные Добавляем Ряд 2 полученные значения: в поле Значения Х числа строки х_j (без пустых ячеек), в поле Значения У числа строки (без пустых ячеек). На графике появились точки, которые следует выделить правой клавишей мыши, в открывшемся подменю в Типе диаграммы выбираем Точечную диаграмму, на которой значения соединены отрезками. Результат приведен на рис.3.3.

Рисунок 3.3. Эмпирическая линия регрессии.

3. По виду эмпирической линии регрессии подбираем уравнение регрессии у=f(х). Для этого можно использовать линии тренда в Microsoft Excel. Для этого при выборе линии тренда в Параметрах указываем Показывать уравнение на диаграмме (рис.3.4)

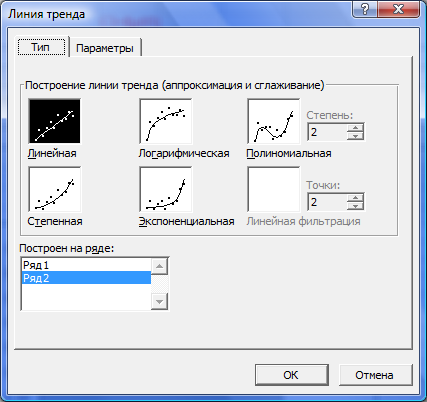
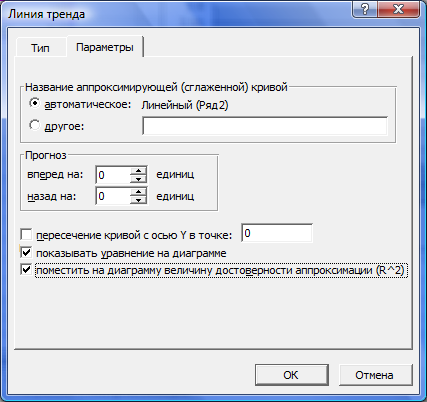
Рисунок 3.4. Использование Параметров Линии тренда.

В Еxcel заложены следующие формулы для расчета линий тренда:

Арифметическая - используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

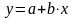(3.3)

где a - координата пересечения оси абсцисс,

b - угол наклона.

Полиномиальная - используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

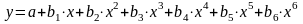(3.4)

где a и b₁ … b₆ — константы.

Логарифмическая - используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

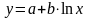(3.5)

где а и b - константы,

ln - функция натурального логарифма.

Экспоненциальная - используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

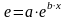(3.6)

где а и b - константы,

e - основание натурального логарифма.

Степенная - используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

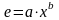(3.7)

где а и b - константы.

Величина R-квадрат

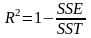(3.8)

где

, (3.9)

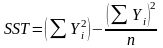(3.10)

Примечание.   Отображаемое вместе с линией тренда значение величины R-квадрат не является корректным. Для логарифмической, степенной и экспоненциальной линий тренда в Microsoft Excel используется несколько видоизмененная модель регрессии.

Итак, аппроксимируем исходные данные с помощью линий тренда Excel. Для этого в подменю полученных значений Добавим линию тренда. В Параметрах указать Показывать уравнения на диаграмме и Поместить на диаграмму величину достоверности аппроксимации. Если наносим несколько линий (как в нашем случае), то желательно их пометить разным цветом. Это выполняется в Виде подменю Формата линии тренда. На рис.3.3 приведены аппроксимирующие функции.

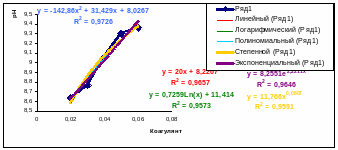
Рисунок 3.5. Аппроксимирующие функции исследуемой зависимости.

Визуальный анализ наложения линий тренда показывает, что аппроксимация логарифмической и степенной также как линейной и экспоненциальной зависимостью практически сливаются. Расчетные значения величины достоверности аппроксимации (R-квадрат) также близки: 0,9573 и 0,9591 для линейной и экспоненциальной зависимостей: 0, 9657 и 0, 9646 для второй пары. Лучшее приближение наблюдается при использовании линии полиномиального тренда второго порядка(R-квадрат 0,9726). Поэтому далее рассмотрим полиномиальные структуры других порядков (рис.3.4).

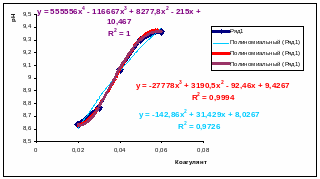
Рисунок 3.6. Аппроксимирующие полиномиальные функции для исследуемой зависимости.

Наилучшим образом исследуемую зависимость аппроксимирует полином 4 поряда (R²=1)

.

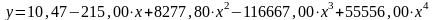4. Для проверки адекватности модели постоим по исходным данным расчетные значения, после чего сравним у^практ и у^расч (табл.3.3).

Таблица 3.3

Сравнительная таблица практических и расчетных значений функции отклика

хj	0,02	0,03	0,04	0,05	0,06
Упракт	8,63	8,77	9,07	9,3	9,37
Урасч	8,64	8,77	9,07	9,3	9,37

Ответ: Представленная зависимость влияния коагулянта на рН раствора может быть описана полиномиальным уравнением 4-го порядка:

Пример 3.2. На основании предыдущего расчета сделано предположение о наличии зависимости между факторами: С1-РН1, РН3, V, Р1; С2-РН1, РН3, V, Р1; С3-РН1, РН3, V, Т, Р1 и взаимовлияние Т-Р1, V, РН1, РН3 и РН3-Р1, РН1. Определить аппроксимирующие функции однофакторных зависимостей исследуемой выборки.

Таблица 3.4

Исследуемая выборка

Время	Т окр.ср	Р1	V	C1	C2	C3	РН1	РН3	Р1
2	188	3,6	3,53	0,5	0,74	0,05	3	2	3,6
4	188	3,57	3,51	0,49	0,7	0,05	3	2	3,57
11	187	3,22	3,08	0,93	0,96	0,07	2	3	3,22
12	187	3,43	3,3	0,88	0,94	0,07	2	3	3,43
13	187	3,43	3,29	0,91	0,96	0,07	2	3	3,43
19	187	3,45	3,4	0,43	0,66	0,05	3	2	3,45
20	187	3,45	3,39	0,43	0,66	0,05	3	2	3,45