
- •«Данные опроса»
- •«Оценивание функции спроса и расчет оптимальной цены»
- •Обработка данных с помощью метода наименьших квадратов(мнк).
- •«Оценивание функции спроса мнк»
- •«Сравнение оптимальных цен»
- •Построение восстановленной функции спроса мнк, используя степенную аппроксимацию.
- •«Сравнение оптимальных цен»
«Сравнение оптимальных цен»
|
|
Прибыль1 |
|
Прибыль2 |
120 |
2500 |
61 880 |
2682 |
67 438,12 |
1000 |
3000 |
42 000 |
3122 |
46 262,68 |
1500 |
3500 |
32 000 |
3372 |
36 003,61 |
2100 |
4000 |
22 800 |
3722 |
25 362,32 |
2700 |
4500 |
16 200 |
3972 |
16 622,11 |
По данным табл. 4 видна разница между оптимальной ценой , найденной исходя только из данных опроса, и ценой , рассчитанной с помощью МНК. Это связано с тем, что респонденты всегда склонны называть круглые числа (например, 2500 руб., а не 2 682руб.), поэтому данные полученные МНК наиболее точные, так как мы исследуем более обширное множество значений, а не только названные значения.
Построение восстановленной функции спроса мнк, используя степенную аппроксимацию.
Приблизим
функцию спроса с помощью степенной
функции:


Пусть
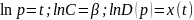
Получим
линейное уравнение:
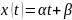
Задача оценивания параметров степенной зависимости сведена к ранее рассмотренной задаче оценивания параметров линейной функции.
Таблица 5
«Оценивание функции спроса на основе использования степенной аппроксимации»
|
|
|
|
D( ) |
x( ) |
x( ) |
|
|
x( ) |
x*( ) |
x( )- x*( ) |
( ) |
[D( ) – ( )] |
|
1 |
500 |
6,21 |
6 |
50 |
3,91 |
23,46 |
37,26 |
231,38 |
145,69 |
4,37 |
-0,46 |
80,73 |
-184,38 |
5666,00 |
2 |
1000 |
6,91 |
4 |
44 |
3,78 |
15,12 |
27,64 |
190,99 |
104,48 |
3,76 |
0,02 |
43,87 |
0,52 |
0,07 |
3 |
1500 |
7,31 |
8 |
40 |
3,69 |
29,52 |
58,48 |
427,49 |
215,79 |
3,40 |
0,29 |
30,70 |
74,40 |
691,92 |
4 |
2000 |
7,60 |
6 |
32 |
3,47 |
20,82 |
45,60 |
346,56 |
158,23 |
3,15 |
0,32 |
23,84 |
48,96 |
399,51 |
5 |
2500 |
7,82 |
5 |
26 |
3,26 |
16,30 |
39,10 |
305,76 |
127,47 |
2,95 |
0,31 |
19,59 |
32,05 |
205,44 |
6 |
3000 |
8,01 |
5 |
21 |
3,04 |
15,20 |
40,05 |
320,80 |
121,75 |
2,79 |
0,25 |
16,68 |
21,60 |
93,31 |
7 |
3500 |
8,16 |
4 |
16 |
2,77 |
11,08 |
32,64 |
266,34 |
90,41 |
2,66 |
0,12 |
14,57 |
5,72 |
8,18 |
8 |
4000 |
8,29 |
3 |
12 |
2,48 |
7,44 |
24,87 |
206,17 |
61,68 |
2,54 |
-0,05 |
12,95 |
-2,85 |
2,71 |
9 |
4500 |
8,41 |
4 |
9 |
2,20 |
8,80 |
33,64 |
282,91 |
74,01 |
2,43 |
-0,24 |
11,68 |
-10,72 |
28,73 |
10 |
5000 |
8,52 |
5 |
5 |
1,61 |
8,05 |
42,60 |
362,95 |
68,59 |
2,34 |
-0,73 |
10,64 |
-28,20 |
159,05 |
∑ |
|
|
|
|
|
155,79 |
381,88 |
2941,37 |
1168,09 |
|
-0,18 |
265,25 |
-42,90 |
SS=7254,92 |
∑/50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
=145,10 |
Найдем оценки параметров α и β:

 9,8576556
9,8576556
Запишем восстановленную зависимость:

Вернемся к степенной функции:

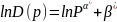
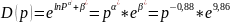 =
=


Рисунок 3: «Выборочная и восстановленная функции»
Необходимо выполнения условия : ∑x( )- x*( ) = 0
Однако сумма по этому столбцу дает -0,18, а не 0. Незначительное отличие от 0 связано с ошибками округления при вычислениях.
Укажем насколько хорошо установлена зависимость, для этого рассчитаем относительную погрешность:
|
 |*100%
|*100%
D(p) |
|
D(p) - |
|[ D(p) - ]/D(p)| |
Погрешность |
50 |
80,73 |
-30,73 |
0,61 |
61,46% |
44 |
43,87 |
0,13 |
0,003 |
0,30% |
40 |
30,70 |
9,30 |
0,23 |
23,25% |
32 |
23,84 |
8,16 |
0,26 |
25,50% |
26 |
19,59 |
6,41 |
0,25 |
24,65% |
21 |
16,68 |
4,32 |
0,21 |
20,57% |
16 |
14,57 |
1,43 |
0,09 |
8,94% |
12 |
12,95 |
-0,95 |
0,08 |
7,92% |
9 |
11,68 |
-2,68 |
0,30 |
29,78% |
5 |
10,64 |
-5,64 |
1,13 |
112,80% |
Максимальная погрешность составила 112,80%
Рассчитаем оптимальную цену:
(
)*
D(
)
= (
)* max
max
 ;
;
 =
=
 (
( )
=
)
=
=
(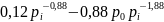 )
;
)
;
( ) = 0 ;
=
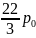
При издержках =120 =880
П=(880-120)*(880)-0,88*19148,89=760*0,0026*19148,89=37838(руб.)
В
табл.4 приведено сравнение оптимальных
цен, найденных с помощью МНК
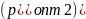 и метода на основе степенной
аппроксимации
).
и метода на основе степенной
аппроксимации
).
Таблица 4


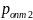
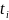
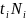
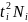
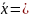 3,12
3,12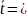 7,64
7,64 =58,84
=58,84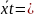 23,37
23,37