Дисперсия света

Дисперсией света называется зависимость показателя преломления вещества от частоты или длины волны света: .

Следствием дисперсии является разложение в спектр белого света при прохождении через призму.

П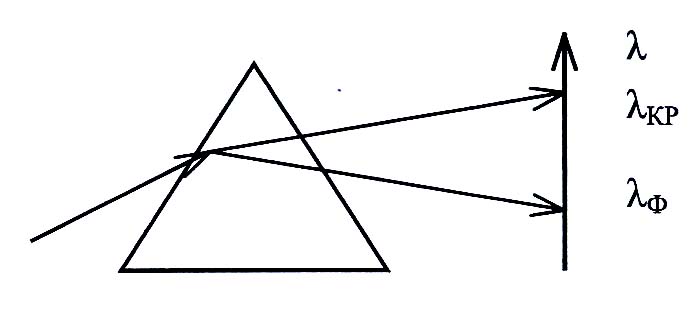 оскольку абсолютный показатель преломления (n) – зависит от длины волны, то волны разных длин после прохождения призмы окажутся отклоненными на разные углы, т.е. белый свет (сложный) разлагается в спектр. Величина называется дисперсией вещества и показывает, как быстро изменяется показатель преломления с длиной волны.

В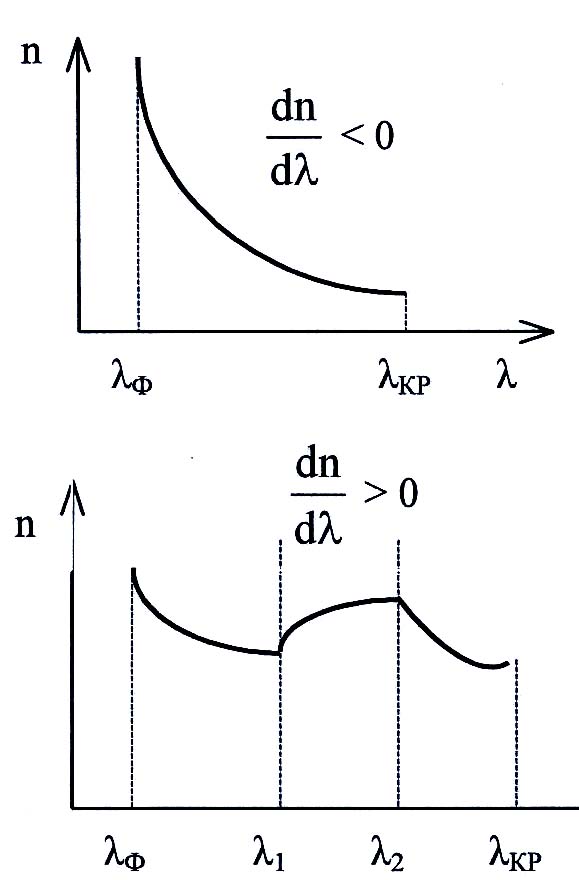 озможны два случая. Если  0 – это нормальная дисперсия, т.е. короткие волны преломляются сильнее, чем длинные.

А поскольку , то значит более длинные волны распространяются в прозрачной среде быстрее, чем короткие.

Если на участке λ₂  λ₁ величина > 0, то это область аномальной дисперсии.

Электронная теория дисперсии света

Из теории Максвелла следует, что , где ε – диэлектрическая проницаемость среды, μ – магнитная проницаемость среды. В оптической области спектра для всех веществ μ ≈ 1, поэтому . Лоренц предложил электронную теорию, в которой дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны. Дисперсия света является следствием зависимости ε от частоты световых волн ω.

Для большинства диэлектриков поляризованность линейно зависит от напряженности электрического поля :

,

где χ – диэлектрическая восприимчивость вещества. По определению ε = 1 + χ, тогда ε = 1 + χ = 1 + . То есть . Рассмотрим колебания одного электрона в атоме. Наведенный дипольный момент электрона р_i = ex, где е – заряд электрона, x – смещение его под действием электрического поля волны. Если концентрация атомов в диэлектрике n₀, то значение поляризованности Р = n₀ р_i = n₀ ex, тогда . Электрическое поле световой волны является гармонической функцией частоты ω: Е = Е₀ cos ωt. Уравнение вынужденных колебаний для простейшего случая (без учета сил сопротивления): , где F₀ = eE₀ – амплитуда силы, действующей на электрон. Решение этого уравнения имеет вид: x = = A cos ωt, где А = – амплитуда колебаний, ω₀ – собственная частота колебаний электрона. Подставляя x и А в уравнение, получим: . Полученное выражение показывает, что n зависит от частоты внешнего поля и подтверждает явление дисперсии.

1. при ω → ω₀, n → ∞ – нормальная дисперсия;

2. при ω → от ω₀ к ∞, n → от – ∞ к 1 – нормальная дисперсия;

3. при ω = ω₀, n → ± ∞, т.е. функция терпит разрыв.

Е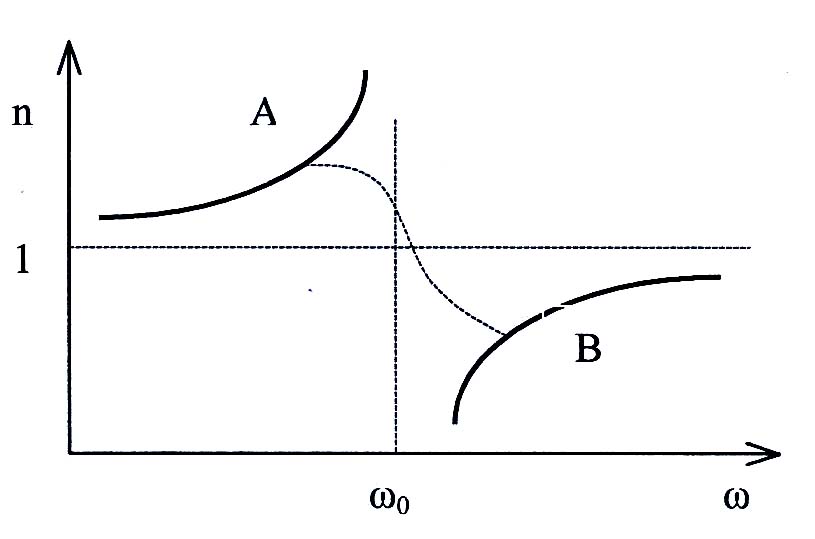 сли учесть влияние сил сопротивления при колебаниях электронов, то график функции n(ω) вблизи ω₀ задается штриховой линией АВ – это область аномальной дисперсии.

Поляризация света. Естественный и поляризованный свет

В электромагнитной волне векторы напряженностей электрического и магнитного полей взаимно перпендикулярны и колеблются перпендикулярно скорости распространения волны, т.е. лучу. Для описания явления поляризации рассматривают поведение вектора , который называется световым вектором. Свет – это суммарное электромагнитное излучение множества атомов, поэтому световая волна характеризуется всевозможными равновероятными колебаниями светового вектора (луч перпендикулярен плоскости рисунка).

С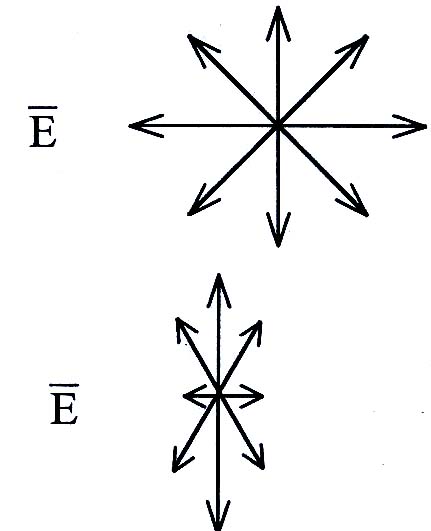 вет с равновероятными ориентациями вектора называется естественным. Если в результате каких-либо внешних воздействий появляется преимущественное направление колебаний вектора , то это – частично поляризованный свет.

Свет, в котором вектор колеблется только в одной плоскости, называется плоско поляризованным. Плоскостью колебаний (плоскостью поляризации) называется плоскость, проходящая через направление колебания светового вектора и направление распространения волны.

П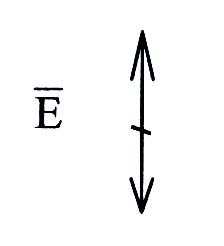 лоско поляризованный свет можно получить из естественного при помощи приборов, называемых поляризаторами. Это кристаллические пластинки, которые свободно пропускают колебания, параллельные плоскости поляризатора (определенная плоскость прибора) и полностью задерживают перпендикулярные ей колебания. Анализатором называют второй поляризатор, стоящий после первого и способный вращаться вокруг направления луча. Он используется для анализа уже поляризованного света.