Интерференция света

Пусть две когерентные монохроматические волны ( = const), накладываясь друг на друга, возбуждают в определенной точке пространства колебания одинакового направления и . Поскольку световая волна является электромагнитной, то под x понимают напряженность электрического или магнитного полей волны. Векторы и взаимно перпендикулярны. Из теории колебаний известно, что результирующее колебание в данной точке также будет гармоническим с частотой , но с другой амплитудой А и начальной фазой .

Для амплитуды результирующего колебания используем метод векторных диаграмм. Из теоремы косинусов:

,

видно, что амплитуда результирующего колебания зависит от разности фаз .

Если волны когерентны, то имеет постоянное во времени значение. Интенсивность света ~ в однородной изотропной среде и интерференционное уравнение примет вид:

.

В точках пространства, где > 0, интенсивность I > ; там где < 0, интенсивность I < .

Т аким образом, при наложении двух (или более) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего, в одних местах возникают максимумы интенсивности, а в других – минимумы. Это явление называется интерференцией света.

Для некогерентных волн разность фаз непрерывно изменяется, поэтому среднее по времени значение и интенсивность результирующей волны всюду одинакова. В случае , она равна . Для когерентных волн изменяется от 1 до – 1, поэтому в максимумах, где = 1, интенсивность , а в минимумах, где = – 1, I = 0.

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две волны, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференционная картина.

Пусть разделение на две когерентные волны происходит в точке 0. До точки М, где наблюдается интерференция, одна волна прошла путь S₁ в среде с показателем преломления . Вторая волна прошла путь S₂ в среде с показателем преломления . В точке М первая волна возбудит колебание , а вторая – колебание .

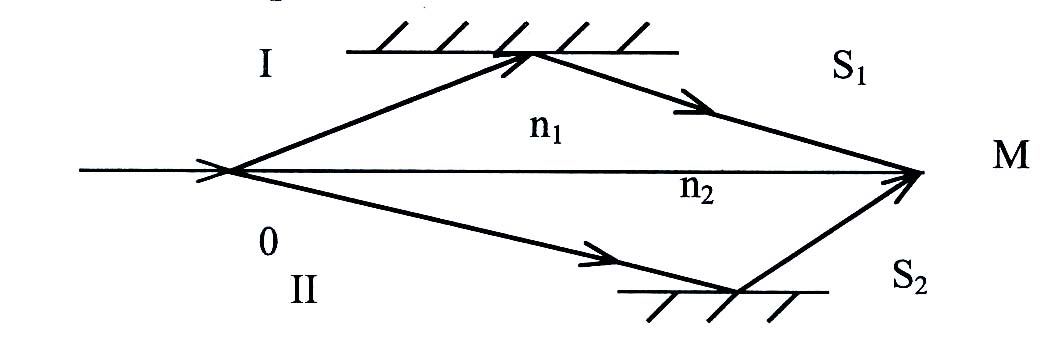
Тогда разность фаз колебаний в точке М:

,

где – оптическая длина пути световой волны в среде с показателем преломления n; – оптическая разность хода двух волн. Связь оптической разности фаз с оптической разностью хода:

,

где – длина волны в вакууме.

Если , то есть равна целому числу волн, то , и колебания в точке М совершаются в одинаковой фазе, значит, в точке М наблюдается интерференционный максимум. Если , равна нечетному числу полуволн, то и колебания в точке М будут происходить в противофазе. Это условие интерференционного минимума.

Расчет интерференционной картины от двух когерентных источников

Расчет интерференционной картины можно провести, используя две узкие параллельные щели и , являющиеся источниками цилиндрических когерентных волн. Интерференция наблюдается в произвольной точке А экрана Э, параллельного обеим щелям и расположенного от них на расстоянии ℓ >> d. Начало отсчета выбрано в точке О, симметричной относительно щелей. Интерференционная картина в случае цилиндрических волн представляет собой чередующиеся светлые и темные полосы. Интенсивность в любой точке А экрана, лежащей на расстоянии x от точки О определяется оптической разностью хода: т.к. n = 1 (вакуум).

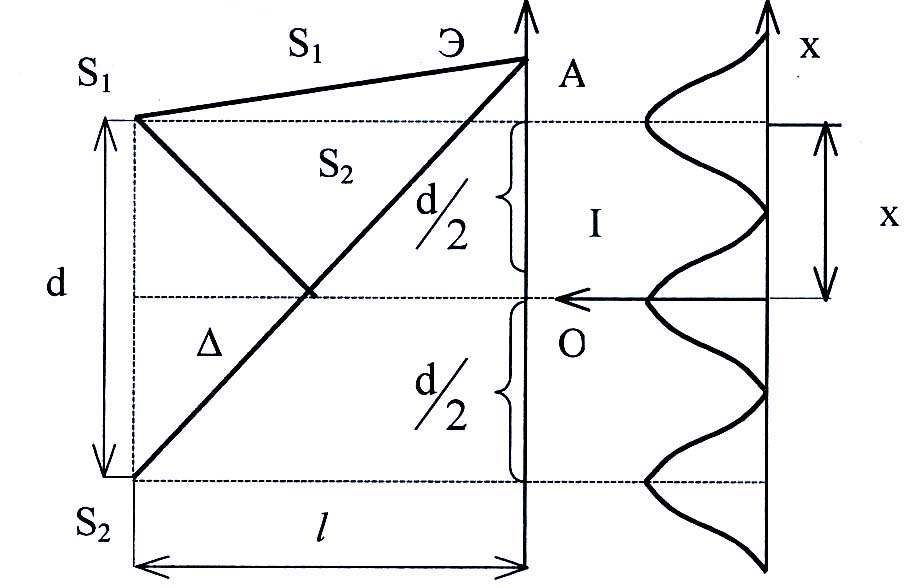
Из рисунка следует, что и .Тогда разность квадратов оптических путей:

Оптическая разность хода: . Из условия >> d или >> x следует, что . Тогда .

Подставляя полученное значение в условие максимума , получим: , т.е. максимумы интенсивности наблюдаются в точках экрана, где .

Подставляя в условие минимума . Получим , т.е. минимумы интенсивности наблюдаются в точках экрана, где . Расстояние между соседними максимумами и минимумами называется шириной интерференционной полосы. Можно показать, что . Величине m = 0 соответствует главный максимум. Максимумы и минимумы, соответствующие значениям m = 1,2,3,… называются максимумами и минимумами первого, второго, третьего и т.д. порядков.