Спин электрона
Кроме орбитальных
магнитного (
)
и механического (
)
моментов электрона, определяющих его
движение по орбите, электрон обладает
собственным механическим моментом
импульса. Он носит название спина -
и не связан с движением электрона в
пространстве. Следствием наличия спина
является существование собственный
магнитный момент
.
Эти моменты являются внутренними
неотъемлемыми свойствами электрона,
такими же, как заряд и масса. Спин может
принимать лишь дискретные значения и
квантуется по закону
,
где
– спиновое квантовое число. Для электрона,
протона и нейрона
,
для фотона
.
Проекция спина
на направление внешнего магнитного
поля квантуется так, что вектор
может принимать только
ориентаций. Значит, для электрона (
)
всего две ориентации.
,
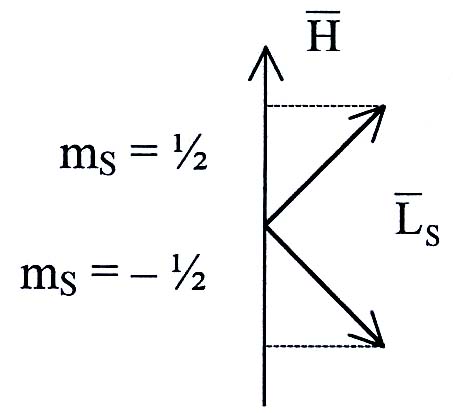
где
– магнитное спиновое квантовое число.
Для электрона оно принимает лишь два
значения
.
Все
элементарные частицы делятся на два
класса.. Частицы с полу целым спином
,
(
;
электроны, протоны, нейроны) называются
фермионами. Частицы с целым спином (
;
-мезоны,
фотоны, фононы) называются бозонами.
Принцип Паули
Распределение
электронов по энергетическим уровням
в атоме подчиняется принципу Паули: в
атоме не может быть более одного электрона
с одинаковым набором четырех квантовых
чисел
и
т.е.
или 1. Поскольку для электрона число
принимает лишь два значения
,
то на любом энергетическом уровне может
находиться не более двух электронов с
разными спинами. Максимальное число
электронов, находящихся в состояниях,
определяемых главным квантовым числом
равно
,
т.е.
-электронов
с
и
-электронов
с
.
Отметим, что принципу Паули подчиняется
распределение по энергетическим
состояниям не только электронов, но и
всех фермионов. Распределение бозонов
принципу Паули не подчиняется.
VI. Физика твердого тела Классическая и квантовая статистики
С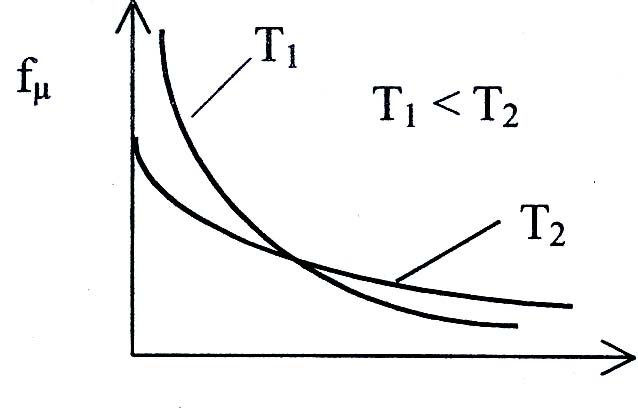
татистическая
физика изучает свойства систем, состоящих
из огромного числа частиц, в которых
проявляются статистические закономерности.
В зависимости от внешних и внутренних
условий частицы системы подчиняются
законам классической или квантовой
механики. Соответственно различают
классическую и квантовую статистики.
Основной задачей любой статистики,
является нахождение функции распределения
частиц системы по тем или иным параметрам
(координаты, энергия, импульс). Классическая
статистика называется статистикой
Максвелла - Больцмана. Здесь частицы
считаются различимыми, а энергия может
принимать как дискретный, так и непрерывный
ряд значений. Примером системы классических
частиц является молекулярный газ. Такие
частицы описываются функцией распределения
Максвелла - Больцмана:
,
где
– химический потенциал, который выражает
изменение свободной энергии системы
при изменении числа частиц на единицу.
По характеру поведения в системе все микрочастицы делятся на две группы: фермионы (частицы с полуцелым спином) и бозоны (частицы с целым спином). С учетом специфики фермионов и бозонов различают две квантовые статистики: квантовую статистику бозонов – статистику Бозе-Эйнштейна и квантовую статистику фермионов – статистику Ферми-Дирака.