V. Атомная физика Теория атома Бора. Постулаты Бора

Резерфорд предложил ядерную модель атома: вокруг положительно заряженного ядра, имеющего заряд ( – порядковый номер элемента), по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Кулоновская сила взаимодействия сообщает электрону центростремительное ускорение. Второй закон Ньютона для электрона, движущегося по окружности: , где и – масса и скорость электрона на орбите радиуса . Недостаток уравнения в том, что оно содержит два неизвестных и . Следовательно, существует бесчисленное множество значений радиусов и скоростей, а значит и энергий, которая может меняться непрерывно, и следовательно, испускаться любая порция энергии. Этому противоречит линейчатый спектр излучения атомов. Попытки построить теорию атома в рамках классической физики не привели к успеху. Первая попытка построить новую квантовую теорию атома была предложена Бором. В основу теории Бор положил два постулата:

I постулат (постулат стационарных состояний). В атоме существуют стационарные (не изменяющиеся во времени) состояния, в которых он не излучает энергии. Стационарным состояниям соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по ним не сопровождается излучением электромагнитных волн. В стационарном состоянии атома электрон должен иметь дискретные квантовые значения момента импульса, удовлетворяющие условию: .

II постулат (правило частот). При переходе электрона с одной стационарной орбиты на другую излучается или поглощается один фотон с энергией , равной разности энергий соответствующих стационарных состояний. – энергии электрона на соответствующих орбитах. Решая совместно уравнение Резерфорда с условием первого постулата Бора, найдем радиус стационарной орбиты электрона , тогда энергия электрона на -ой стационарной орбите: . Полученные энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения , где – главное квантовое число. Состояние атома для значения главного квантового числа называется основным или нормальным состоянием; если > 1 – состояния называются возбужденными.

В квантовой механике состояние электрона в атоме водорода ( ) описывается волновой функцией , удовлетворяющей стационарному уравнению Шредингера:

.

Потенциальная энергия взаимодействия электрона с ядром , тогда 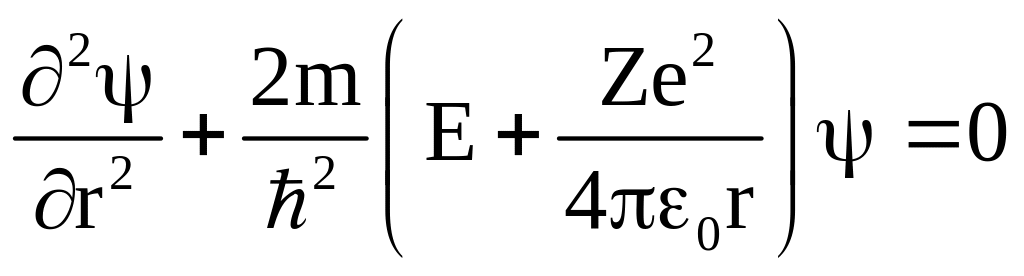. Решение этого уравнения позволяет найти собственные значения энергии электрона:

.

Энергия принимает дискретные отрицательные значения. Выражение для совпадает с формулой, полученной Бором для энергии электрона в атоме водорода, однако, если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии вытекают непосредственно из решения уравнения Шредингера.

Квантовые числа

Квантовые числа – это целые или полу целые числа, определяющие возможные дискретные значения физических величин системы, подчиняющиеся квантовым законам.

Главное квантовое число , определяет энергетические уровни электрона в атоме, Электроны со значениями энергии, соответствующими главному квантовому числу образуют К-оболочку; со значениями – L-оболочку, – М-оболочку, и т.д.

Из решения уравнения Шредингера вытекает, что механический орбитальный момент импульса электрона квантуется, принимая дискретные значения, определяемые формулой , где – орбитальное квантовое число. Оно определяет форму орбиты и принимает значения , т.е. всего значений. Например, при , Если – это s-электрон, при – р-электрон, при – d-электрон, и т.д.

И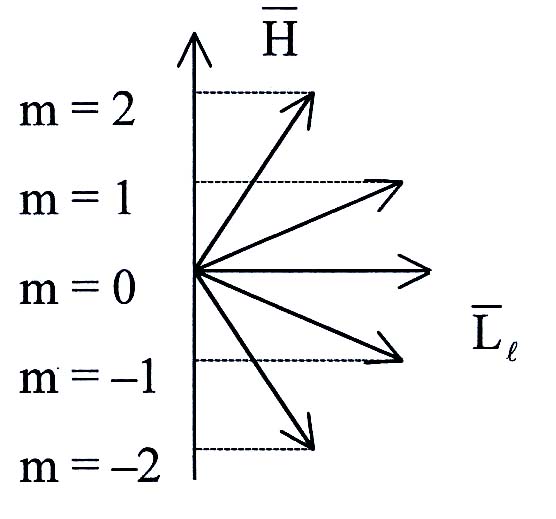 з решения уравнения Шредингера следует, что вектор орбитального момента импульса электрона может быть только так ориентирован в пространстве, когда его проекция на направление внешнего магнитного поля принимает только квантованные значения , где – магнитное квантовое число. Оно определяет проекцию на направление внешнего магнитного поля и характеризует ориентацию плоскости электронной орбиты в пространстве, принимая значения , всего значений ориентаций.

Хотя энергия электрона и зависит только от квантового числа , но каждому собственному значению энергии соответствует несколько собственных функций , отличающихся значениями и . Значит, атом водорода может иметь одно и то же значение энергии, находясь в различных состояниях. Число различных состояний, соответствующих главному квантовому числу , равно . Состояния с одинаковым значением энергии называются вырожденными, а число таких состояний с одинаковыми значениями энергии называется кратностью вырождения соответствующего уровня. Каждый уровень энергии водородоподобного атома имеет кратность вырождения, равную .