2. Моноиды

Непустое множество, рассматриваемое вместе с ассоциативной бинарной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом. Более точно: алгебраическая система 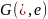, где * -- ассоциативная бинарная операция, а -- выделенный элемент (0-арная операция), который нейтрален относительно *, называется моноидом.

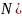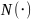Приведем примеры: 1) – множество натуральных чисел со сложением. Эта полугруппа будет коммутативной, ибо сложение – коммутативная операция; 2) – множество натуральных чисел относительно умножения. Эта полугруппа также будет коммутативной. 3) Множество всех целочисленных матриц второго порядка 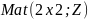относительно умножения (некоммутативная полугруппа) ; 4) то же самое множество относительно сложения.

В примерах выше 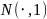– моноид и относительно умножения и единичной матрицы 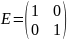также моноид. Однако не будет моноидом, так как нет нейтрального элемента (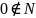 ). В связи с этим образуем моноид

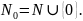
В моноиде элемент 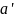называется обратным (противоположным в случае, когда операция – сложение) к элементу , если 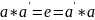. Обратный элемент, если он существует единственен. Действительно, предположив существование еще одного обратного элемента 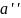к элементу , будем иметь:

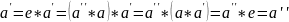
Если обратен к , то обратен к . Это свойство сразу следует из определения обратного элемента. Если обратен к , а 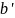обратен к , то обратен к 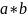. Проверка:

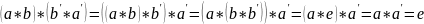
Здесь в первых двух равенствах применена ассоциативность операции *. Аналогично доказывается, что .

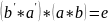Заметим, что нейтральный элемент всегда обратим и обратным к нему служит сам он. Назовем элемент 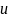моноида инволюцией, если 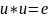. Например, в моноиде квадратных матриц относительно умножения диагональные матрицы с элементами 0, ± 1 будут все инволюциями. В группе движений плоскости инволюциями будут отражения относительно прямой.

3. Группы

Группа -- это моноид, в котором каждый элемент обратим. Более точное определение таково: алгебраическая система 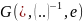, где * -- бинарная, 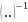– унарная и -- 0-арная операции называется группой, если выполнены следующие аксиомы

Г1. -- ассоциативность *,

Г2. 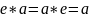для любого (нейтральность ),

Г3. 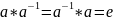(обратимость любого элемента)

Если операция * к тому же и коммутативна, т.е. выполнена аксиома

Г4. ,

то группа G называется абелевой. В этом случае операция * часто обозначается плюсом и называется сложением.

В группе уравнение x*g=h так же как и уравнение g*x=h всегда имеют решения. А именно, первое уравнение имеет корень 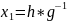, а второе – 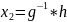и эти корни не обязаны совпадать.

4. Кольца

Множество R с двумя бинарными операциями сложения и умножения, унарной о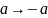перацией перехода к противоположному элементу, 0-арной операцией 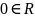называется кольцом, если

К1. 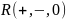является абелевой группой;

К2. R(⋅ ) -- полугруппа;

К3. Умножение дистрибутивно относительно сложения:

и

Если дополнительно операция умножения коммутативна, т.е. выполняется аксиома

К4.

то R называется коммутативным кольцом. Если же дополнительно, имеется единица -- нейтральный элемент относительно умножения, то R называется кольцом с единицей.

Кольцо, в котором выполняется тождество

К5.

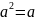
называется булевым. Оно автоматически будет коммутативным

ПРИМЕРЫ 1. Множество, состоящее из одного нуля является (нулевым) кольцом.

2. Кольцо целых чисел ℤ коммутативно и с единицей.

3. Все четные числа 2ℤ образуют коммутативное кольцо, но уже без единицы.

4. Все десятичные рациональные дроб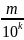и (m∈ ℤ ,k∈ ℕ_0) образуют коммутативное кольцо с единицей.

5. Множество квадратных n×n-матриц c элементами из какого-либо кольца R (обозначение -- Mat(n×n; R) ) будет кольцом. Если R имеет единицу 1, то и Mat(n×n;R) имеет единичную матрицу – E=diag(1,…,1).