§ 4. Проверка статистических гипотез Использование Мастера функций

Гипотеза о равенстве дисперсий двух генеральных совокупностей

Одной из важных задач теории статистических гипотез является гипотеза о равенстве математических ожиданий двух генеральных совокупностей. Функция, используемая для этого (см. ниже), требует указания одного из трех типов: Парный тип, используют для одной и той же выборки: до и после эксперимента. Двухвыборочный тип с равными дисперсиями (гомоскедастический) используют, если дисперсии равны и Двухвыборочный с неравными дисперсиями (гетероскедастический), если дисперсии не одинаковы. Поэтому, если дисперсии неизвестны, сначала необходимо проверить гипотезу о равенстве дисперсий двух генеральных совокупностей, чтобы выбрать нужный тип.

Для этого служит функция ФТЕСТ(массив1;массив2). Данная функция выдает результат F-теста. F-тест возвращает одностороннюю вероятность того, что дисперсии аргументов массив1 и массив2 различаются несущественно. Эта функция используется для того, чтобы определить, имеют ли две выборки различные дисперсии или дисперсии одинаковы.

Синтаксис функции

ФТЕСТ(массив1;массив2) (рис. 4.1)

Массив1 – это первый массив или интервал данных.

Массив2 – это второй массив или интервал данных.

Демонстрационный пример 4А

Для использования ФТЕСТа введите в блок А1:А10 числа от 10 до 100 с шагом 10, введите в блок В1:В10 числа от 15 до 195 с шагом 20. Выдвинем основную гипотезу о равенстве дисперсий этих совокупностей и альтернативную – о том, что . Установите курсор в ячейку Е1, вызовите Мастер функций, выберите функцию ФТЕСТ, в числовое поле Массив1 введите блок А1:А10 (рис. 4.1), в числовое поле Массив2 введите блок В1:В10 и нажмите Ок.

Рис. 4.1

В ячейке Е1 получите результат ФТЕСТа 0,051, что означает: вероятность равенства дисперсий данных генеральных совокупностей равна 5,1 %. Этого недостаточно, чтобы утверждать, что дисперсии одинаковы.

Вывод: ГИПОТЕЗА о равенстве дисперсий двух генеральных совокупностей отвергается и принимается альтернативная ей о том, что .

Гипотеза о равенстве математических ожиданий двух генеральных совокупностей

Функция ТТЕСТ определяет вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ используется, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.

Синтаксис функции (рис. 4.2):

ТТЕСТ(массив1;массив2;хвосты;тип)

Массив1 – первое множество данных.

Массив2 – второе множество данных.

Хвосты – число хвостов распределения. Если хвосты = 1, то функция ТТЕСТ использует одностороннее распределение. Если хвосты = 2, то функция ТТЕСТ использует двустороннее распределение (на практике чаще используется двустороннее распределение).

Тип – вид исполняемого t-теста.

Тип	Выполняемый тест
1.	Парный
2.	Двухвыборочный с равными дисперсиями (гомоскедастический)
3.	Двухвыборочный с неравными дисперсиями (гетероскедастический)

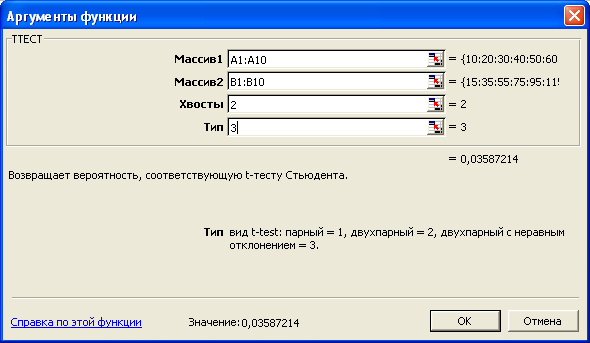
Рис. 4.2

Парный тип используют для одной и той же выборки: до и после эксперимента. Двухвыборочный тип с равными дисперсиями (гомоскедастический) используют, если дисперсии равны и последний тип, если дисперсии не одинаковы.

Демонстрационный пример 4Б

Для использования ТТЕСТа введите в блок А1:А10 числа от 10 до 100 с шагом 10, введите в блок В1:В10 числа от 15 до 195 с шагом 20. Мы уже проверили равенство дисперсий этих двух совокупностей и выяснили, что дисперсии не равны. Выдвинем основную гипотезу о равенстве математических ожиданий этих совокупностей и альтернативную – о том, что они не равны. Установите курсор в ячейку Е1, вызовите Мастер функций, выберите функцию ТТЕСТ, в числовое поле Массив1 введите блок А1:А10 (рис. 4.2), в числовое поле Массив2 введите блок В1:В10, в поле Хвосты число 2, в поле Тип число 3, так как дисперсии не одинаковы.

В ячейке Е1 получите результат ТТЕСТа 0,03587, что означает: вероятность равенства математических ожиданий данных генеральных совокупностей равна около 3,6 %. Этого недостаточно, чтобы утверждать, что данные выборки принадлежат одной генеральной совокупности.

Вывод: ГИПОТЕЗА о равенстве двух математических ожиданий отвергается и принимается альтернативная ей о том, что они не равны.