
- •1 Определённый интеграл
- •1. Задачи, приводящие к понятию определённого интеграла.
- •Площадь криволинейной трапеции.
- •1.2. Понятие определенного интеграла.
- •1.3. Теорема существования определенного интеграла (без доказательства).
- •1.4. Основные свойства определенного интеграла.
- •2.Произвольная от определённого интеграла по переменному верхнему пределу.
- •3. Формула Ньютона-Лейбница.
- •4. Интегрирование по частям в определенном интеграле.
- •5. Несобственные интегралы
- •5.2 Несобственные интегралы от разрывных функций
- •5.3Интегралы, зависящие от параметра. Рассмотрим интеграл вида
- •Бета-функция.
- •Приложения определенного интеграла.
- •6. Геометрические приложения определенных интегралов.
- •6.1. Вычисление площадей плоских фигур.
- •6.2. Длина дуги.
- •6.3.Вычисление объёмов тел вращения.
- •6.4. Вычисление объемов тел по известным поперечным сечениям
- •6.5.Площадь поверхности вращения.
- •7. Приложения определенных интегралов к решению задач физики.
- •7.1.Путь пройденный телом
- •7.2.Работа силы
- •7.3. Количество электричества.
- •7.4. Вычисление давления
- •7.5. Кинематическая энергия
- •7.6. Статический момент.
- •7.7.Координаты центра тяжести.
- •8.Тестовые задания для самостоятельной работы.
- •9. Физические задачи для самостоятельной работы
- •10. Приближенные методы вычисления определенных интегралов.
- •450062, Республика Башкортостан, г. Уфа, ул. Космонавтов,1
4. Интегрирование по частям в определенном интеграле.
Ранее
нами была установлена формула
интегрирования по частям для неопределенных
интегралов. Аналогичную формулу можно
установить и для определенных интегралов.
Пусть функции
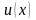 и
и
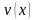 имеют непрерывные производные на отрезке
.
Тогда справедлива формула:
имеют непрерывные производные на отрезке
.
Тогда справедлива формула:
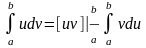 -формула
интегрирования по частям для определенного
интеграла.
-формула
интегрирования по частям для определенного
интеграла.
Докажем эту формулу:
Действительно
на отрезке
имеем;
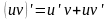 Интегрируем обе части этого тождества
в пределах от a
до b:
Интегрируем обе части этого тождества
в пределах от a
до b:
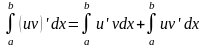 ;
или
;
или
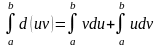 ;
откуда имеем
;
откуда имеем
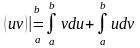 ;
;
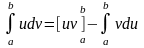 .
Что и требовалось доказать.
.
Что и требовалось доказать.
Доказанная формула
сводит вычисление интеграла
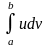 к вычислению интеграла
к вычислению интеграла
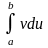 ,
который в ряде случаев может оказаться
более простым, чем первоначальный.
Практика применения этой формулы почти
такая же, что и для соответствующей
формулы в теории неопределенных
интегралов.
,
который в ряде случаев может оказаться
более простым, чем первоначальный.
Практика применения этой формулы почти
такая же, что и для соответствующей
формулы в теории неопределенных
интегралов.
Пример4.1:Вычислить:
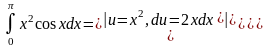
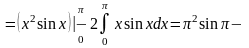
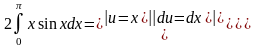

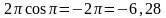 Часто здесь бывает удобно применить,
как и в случае вычисления неопределенного
интеграла, замену переменной путем
введения вместо старой переменной новой
переменной t,
связанной со старой соотношением
Часто здесь бывает удобно применить,
как и в случае вычисления неопределенного
интеграла, замену переменной путем
введения вместо старой переменной новой
переменной t,
связанной со старой соотношением
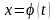 .
.
Итак,
введем новую переменную
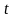 ,
положив
.
Докажем относительно такой замены
следующую теорему:
,
положив
.
Докажем относительно такой замены
следующую теорему:
Пусть выполняются следующие условия:
Функция
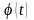 определена и непрерывна на отрезке
определена и непрерывна на отрезке
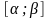
При изменении на значения функции не выходят за пределы отрезка . При этом
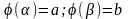
Функция на отрезке имеет непрерывную производную
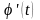
Тогда имеет место равенство:
 (4.1)
(4.1)
(называемое формулой замены переменной под знаком определенного интеграла)
Доказательство: Пусть -какая-либо первообразная для функции на , так что . Тогда по формуле Ньютона-Лейбница имеем:
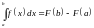 (4.2)
(4.2)
Рассмотрим
на
функцию
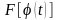 переменной
.
Эта функция сложная.
переменной
.
Эта функция сложная.
Вычислим её производную по формуле дифференцирования сложной функции:
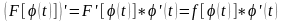
Отсюда
следует, что функция
является первообразной для
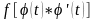 на отрезке
.
А тогда по формуле Ньютона-Лейбница
(которая здесь применима, т.к. функция
на отрезке
.
А тогда по формуле Ньютона-Лейбница
(которая здесь применима, т.к. функция
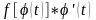 непрерывна на
)
имеем:
непрерывна на
)
имеем:
 но по условию
.
но по условию
.
Поэтому предыдущее
равенство можно переписать и так:
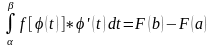 .
(3)
.
(3)
Сопоставляя равенства (2) и (3), мы и получим доказываемую формулу:
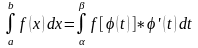
Формула
(4.1) сводит вычисление интеграла
к вычислению интеграла
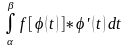 .
.
При пользовании ею следует функцию стараться выбирать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.
Пределы
 и
и
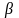 нового интеграла определяются из
уравнений:
нового интеграла определяются из
уравнений:
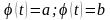 каждое из этих уравнений может иметь
несколько корней, при этом за
можно принять любой корень уравнения
каждое из этих уравнений может иметь
несколько корней, при этом за
можно принять любой корень уравнения
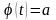 ,
а за
-любой
корень уравнения
,
а за
-любой
корень уравнения
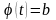 ,
лишь бы выполнялись условия 2) и 3), при
которых установлена формула (4.1).
,
лишь бы выполнялись условия 2) и 3), при
которых установлена формула (4.1).
Условие 2) окажется, в частности, наверняка выполненным, если функция будет монотонной на . Поэтому на практике замену переменной часто осуществляют с помощью монотонных функций, тем более что при применении формулы (4.1) оперировать с такими функциями проще, чем с немонотонными.
Если
функция
не может принимать значений, равных
пределам интегрирования
и
,
то она не может служить для выполнения
замены переменной в этом интеграле.
Так, например, нельзя, очевидно,
преобразовать в интеграле
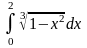 подынтегральную функцию с помощью
подстановки:
подынтегральную функцию с помощью
подстановки:
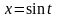 .
.
Отметим одну важную особенность формулы (4.1):
Вычисляя
неопределенный интеграл
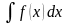 с помощью замены переменной
,
мы должны были, найдя
с помощью замены переменной
,
мы должны были, найдя
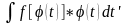 ,
ещё вернуться затем к прежней переменной
.
,
ещё вернуться затем к прежней переменной
.
