5.7. Ортогональные преобразования

Рассмотрим свойства матрицы перехода от одного ортонормированного базиса к другому ортонормированному базису в пространстве Е_n. Введем понятие ортогональной матрицы.

Определение.МатрицаТс вещественными элементами называется ортогональной, еслит.е..

Из определения следует, что ортогональная матрица всегда невырожденная, так как и, то.

Основные свойства ортогональной матрицы.

1. Матрица, обратная ортогональной, также ортогональна.

Пусть Т– ортогональная матрица, т.е.. Тогда, т.е.. Значит, матрица– ортогональна.

2. Матрица ортогональна тогда и только тогда, когда ее элементы удовлетворяют равенствам

.

Линейное преобразование Y=ТХс ортогональной матрицейТназывается ортогональным. Так как, то ортогональное преобразование всегда невырожденное.

Теорема.Ортогональное преобразование координат не изменяет скалярного произведения векторов.

Доказательство.Рассмотрим линейный оператор, соответствующий матрицеТ, и два произвольных вектораиизЕ_n. Их образы обозначим черези, т.е.,. Тогда.

Поэтому .

Следствие 1.Ортогональное преобразование не меняет норм векторов и углов между векторами.

Следствие 2.Ортогональное преобразование переводит ортонормированный базис в ортонормированный.

Следствие 3.МатрицаТ перехода от одного ортонормированного базиса к другому ортонормированному базису является ортогональной.

Следствие 4.МатрицаТ, приводящая симметричную матрицуАк диагональному виду, является ортогональной.

5.8. Выпуклые множества

Рассмотрим совместную систему линейных уравнений

(5.8.1)

у которой ранг r матрицыменьшеn, и пустьk=n-r.

Определение.Множество точекизЕ_n, координаты которых удовлетворяют системе уравнений (5.8.1), называетсяk-мерной плоскостью. Одномерные плоскости называются прямыми, а (n-1)-мерные плоскости – гиперплоскостями.

Очевидно, что каждую гиперплоскость можно задать всего одним линейным уравнением:

.

В трехмерном пространстве Е₃гиперплоскости – это обычные плоскости, а вЕ₂– это прямые.

Определение.ОтрезкомвЕ_n, соединяющим точки, называется множество таких точек, что

Точки называются концами отрезка.

Определение.МножествоХпространстваЕ_nназывается выпуклым, если вместе с любыми двумя точкамиему принадлежит и соединяющих их отрезок.

Выпуклость множества Хозначает, что изследуетдля всех. Например, вЕ₂выпуклый отрезок, полупрямая, круг, треугольник, полуплоскость и вся плоскость.

Определение.МножествоХточек пространстваЕ_nназывается ограниченным, если координаты всех его точекв некотором базисе ограничены.

Пусть в пространстве задана гиперплоскость . Все точки изЕ_nразбиваются этой гиперплоскостью на два полупространства:Х₁ – множество точек, для которыхи– множество точек, для которых.

Теорема. Каждое полупространство пространства Е_n является выпуклым множеством.

Доказательство.Пусть точкииизЕ_nпринадлежат, например, полупространствуХ₁. Тогда

Если – произвольная точка отрезка, то

Для этой точки имеем:

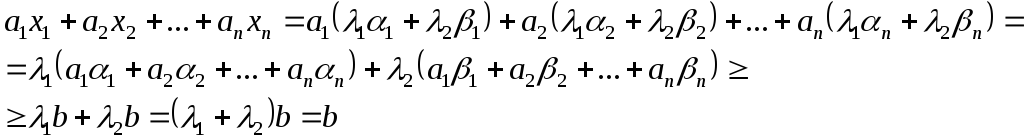
т.е. произвольная точка отрезкапринадлежитХ₁. Теорема доказана.

Теорема. Пересечение любого числа выпуклых множеств есть множество выпуклое.

Доказательство.Пусть– выпуклые множества вЕ_n. Еслисостоит из одной точки, то оно выпукло. Если более чем из одной, то пусть– любые две из них. Тогдаи, так как все множествавыпуклы, тои, следовательно,, что и требовалось доказать.

Из данной теоремы следует, что гиперплоскость как пересечение выпуклых множеств Х₁ и Х₂, является выпуклым множеством. Каждая k-мерная плоскость в Е_n также выпукла.

Пусть в Е_nданыmполупространств, определяемых неравенствами

.

(5.8.2)

Пересечение этих полупространств, называемое выпуклой многогранной областью, определяет множество решений системы линейных неравенств (5.8.2). Если это пересечение ограничено, оно называется выпуклым многогранником в Е_n.

Определение.Последовательностьточек вЕ_nсходится к точкепри, если

.

Множество называетсяокрестностью точки.

Определение.Множествоназывается замкнутым, если оно содержит все свои предельные точки.

Определение.ТочкаизЕ_nназывается внутренней точкой множестваХ, если существует такая ее-окрестность, все точки которой принадлежат множествуХ.

Определение.ТочкаизЕ_nназывается граничной точкой множестваХ, если любая ее-окрестность содержит как точки, принадлежащие множествуХ, так и точки, ему не принадлежащие. Множество, состоящее из всех граничных точек множестваХ, называется границей множестваХ.

Определение.Точканазывается крайней точкой (вершиной), если вХне существует точек, что.

Для круга любая точка ограничивающей его окружности является крайней. Крайними точками являются все вершины выпуклого многогранника.

Определение.Точканазывается выпуклой комбинацией точек, если существуют такие числа, чтопри условии.

Например, любая внутренняя точка круга является выпуклой комбинацией концов хорды, проходящей через эту точку.

Теорема (о представлении). Любая точкавыпуклого замкнутого, ограниченного множестваможет быть представлена в виде выпуклой комбинации конечного числа крайних точек этого множества.

Пример.Используя теорему о представлении, выразить точкув виде выпуклой комбинации крайних точек множества, заданного системой неравенств

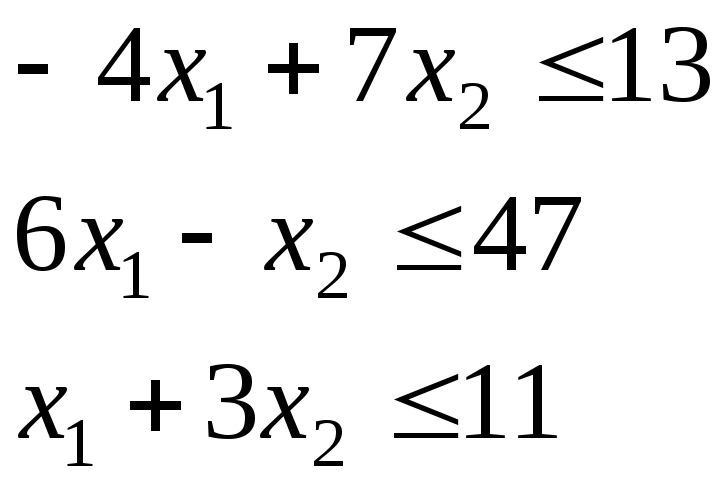
Р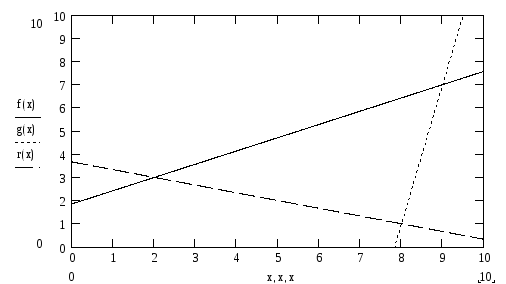ешение.Очевидно, что множествоХвыпукло. МножествоХ(рис.5.1)

представляет собой треугольник с вершинами . На основании теоремы о представлении точкуможно представить в виде следующей выпуклой комбинации:

.

В координатной форме получим два уравнения:

Добавляя к данной системе условие , получим систему трех линейных уравнений с тремя неизвестными. Решая систему методом Жордана-Гаусса, получаем

,

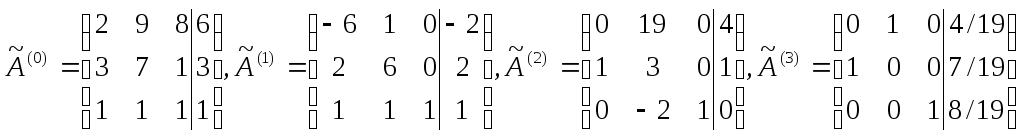откуда

Все эти коэффициенты удовлетворяют условию неотрицательности: . Поэтому искомое представление имеет вид.